Geometry Calibration in Tomography with a Differentiable Ray-Based Model

Geometric misalignments between the nominal and true acquisition parameters in tomography degrade reconstructions. We propose a framework that jointly reconstructs the volume and calibrates the acquisition geometry for arbitrary source--detector configurations. The core of our framework is an x-ray transform operator whose gradients with respect to the acquisition geometry can be efficiently computed with a ray-tracing method of structure and computational complexity similar to those of the forward operator. We represent the volume in a B-spline basis to provide a continuously differentiable model. This results in a better-behaved optimization landscape compared to voxel-based representations. We validate our framework with CT, micro-CT, nano-CT, and positron emission tomography data under a variety of geometric misalignments.

SplineSplat: 3D Ray Tracing for Higher-Quality Tomography

We propose a method to efficiently compute tomographic projections of a 3D volume represented by a linear combination of shifted B-splines. To do so, we propose a ray-tracing algorithm that computes 3D line integrals with arbitrary projection geometries. One of the components of our algorithm is a neural network that computes the contribution of the basis functions efficiently. In our experiments, we consider well-posed cases where the data are sufficient for accurate reconstruction without the need for regularization. We achieve higher reconstruction quality than traditional voxel-based methods.

How accurate is mechanobiology?

Mechanobiology is gaining more and more traction as the fundamental role of physical forces in biological function becomes clearer. Forces at the microscale are often measured indirectly using inverse problems such as Traction Force Microscopy because biological experiments are hard to access with physical probes. In contrast with the experimental nature of biology and physics, these measurements do not come with error bars, confidence regions, or p-values. The aim of this manuscript is to publicize this issue and to propose a first step towards a remedy in the form of a general reconstruction framework that enables hypothesis testing.

Convex quantization preserves logconcavity

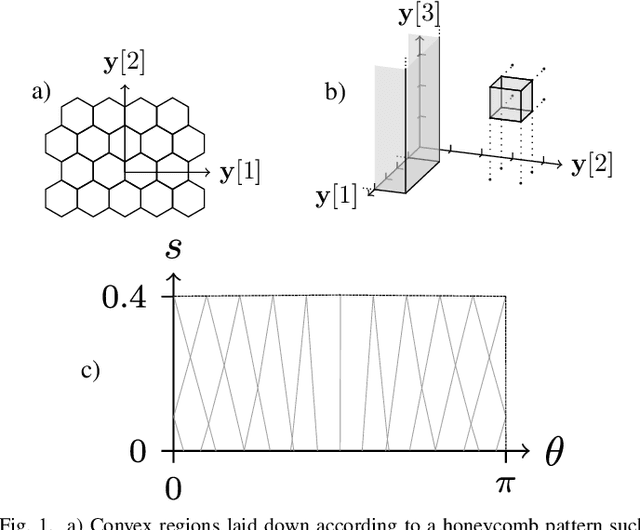
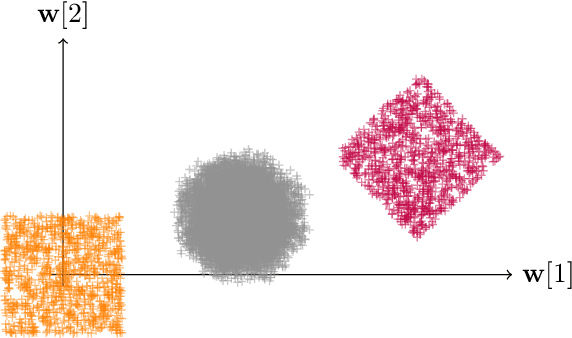
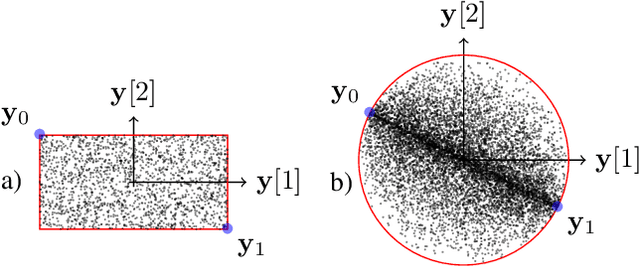
Much like convexity is key to variational optimization, a logconcave distribution is key to amenable statistical inference. Quantization is often disregarded when writing likelihood models: ignoring the limitations of physical detectors. This begs the questions: would including quantization preclude logconcavity, and, are the true data likelihoods logconcave? We show that the same simple assumption that leads to logconcave continuous data likelihoods also leads to logconcave quantized data likelihoods, provided that convex quantization regions are used.

Artifacts in optical projection tomography due to refractive index mismatch: model and correction

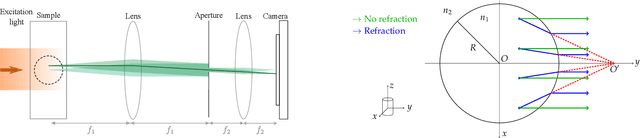
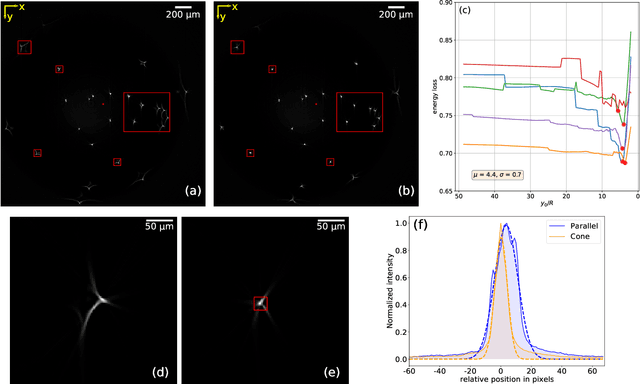
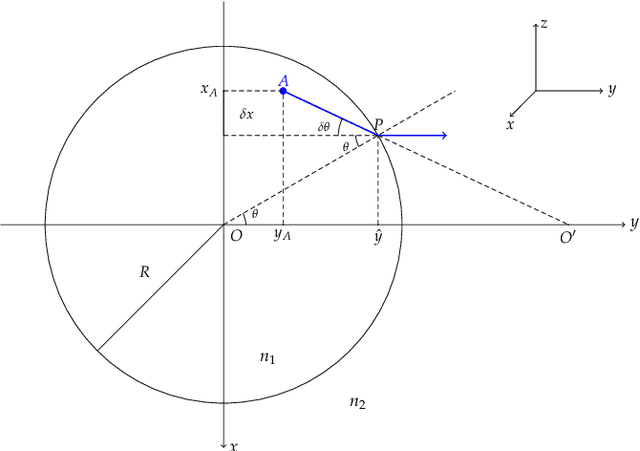
Optical Projection Tomography (OPT) is a powerful tool for 3D imaging of mesoscopic samples, thus of great importance to image whole organs for the study of various disease models in life sciences. OPT is able to achieve resolution at a few tens of microns over a large sample volume of several cubic centimeters. However, the reconstructed OPT images often suffer from artifacts caused by different kinds of physical miscalibration. This work focuses on the refractive index (RI) mismatch between the rotating object and the surrounding medium. We derive a 3D cone beam forward model to approximate the effect of RI mismatch and implement a fast and efficient reconstruction method to correct the induced seagull-shaped artifacts on experimental images of fluorescent beads.