Fronthaul Quantization-Aware MU-MIMO Precoding for Sum Rate Maximization

This paper considers a multi-user multiple-input multiple-output (MU-MIMO) system where the precoding matrix is selected in a baseband unit (BBU) and then sent over a digital fronthaul to the transmitting antenna array. The fronthaul has a limited bit resolution with a known quantization behavior. We formulate a new sum rate maximization problem where the precoding matrix elements must comply with the quantizer. We solve this non-convex mixed-integer problem to local optimality by a novel iterative algorithm inspired by the classical weighted minimum mean square error (WMMSE) approach. The precoding optimization subproblem becomes an integer least-squares problem, which we solve with a new algorithm using a sphere decoding (SD) approach. We show numerically that the proposed precoding technique vastly outperforms the baseline of optimizing an infinite-resolution precoder and then quantizing it. We also develop a heuristic quantization-aware precoding that outperforms the baseline while having comparable complexity.

Modelling the nanopore sequencing process with Helicase HMMs

Recent advancements in nanopore sequencing technology, particularly the R10 nanopore from Oxford Nanopore Technology, have necessitated the development of improved data processing methods to utilize their potential for more than 9-mer resolution fully. The processing of the ion currents predominantly utilizes neural network-based methods known for their high basecalling accuracy but face developmental bottlenecks at higher resolutions. In light of this, we introduce the Helicase Hidden Markov Model (HHMM), a novel framework designed to incorporate the dynamics of the helicase motor protein alongside the nucleotide sequence during nanopore sequencing. This model supports the analysis of millions of distinct states, enhancing our understanding of raw ion currents and their alignment with nucleotide sequences. Our findings demonstrate the utility of HHMM not only as a potent visualization tool but also as an effective base for developing advanced basecalling algorithms. This approach offers a promising avenue for leveraging the full capabilities of emerging high-resolution nanopore sequencing technologies.

Marginalized Beam Search Algorithms for Hierarchical HMMs

Inferring a state sequence from a sequence of measurements is a fundamental problem in bioinformatics and natural language processing. The Viterbi and the Beam Search (BS) algorithms are popular inference methods, but they have limitations when applied to Hierarchical Hidden Markov Models (HHMMs), where the interest lies in the outer state sequence. The Viterbi algorithm can not infer outer states without inner states, while the BS algorithm requires marginalization over prohibitively large state spaces. We propose two new algorithms to overcome these limitations: the greedy marginalized BS algorithm and the local focus BS algorithm. We show that they approximate the most likely outer state sequence with higher performance than the Viterbi algorithm, and we evaluate the performance of these algorithms on an explicit duration HMM with simulation and nanopore base calling data.

Optimized Precoding for MU-MIMO With Fronthaul Quantization

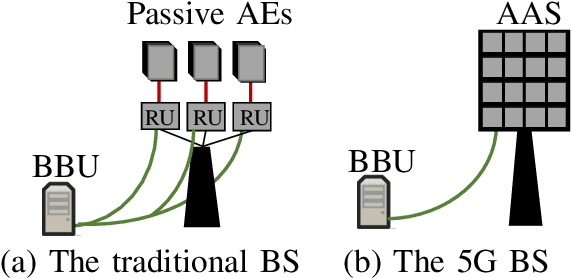
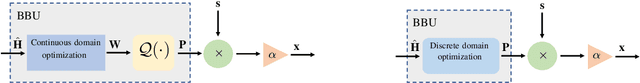
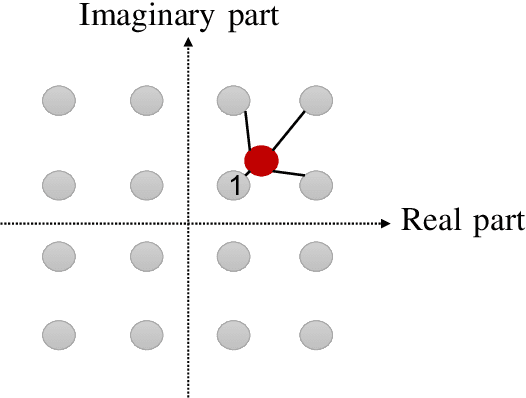
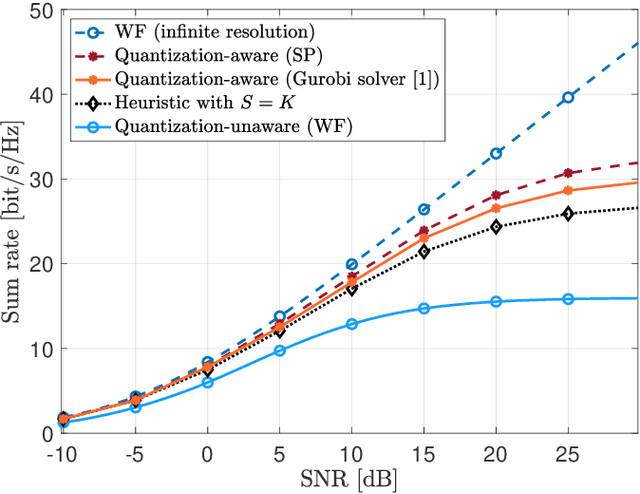
One of the first widespread uses of multi-user multiple-input multiple-output (MU-MIMO) is in 5G networks, where each base station has an advanced antenna system (AAS) that is connected to the baseband unit (BBU) with a capacity-constrained fronthaul. In the AAS configuration, multiple passive antenna elements and radio units are integrated into a single box. This paper considers precoded downlink transmission over a single-cell MU-MIMO system. We study optimized linear precoding for AAS with a limited-capacity fronthaul, which requires the precoding matrix to be quantized. We propose a new precoding design that is aware of the fronthaul quantization and minimizes the mean-squared error at the receiver side. We compute the precoding matrix using a sphere decoding (SD) approach. We also propose a heuristic low-complexity approach to quantized precoding. This heuristic is computationally efficient enough for massive MIMO systems. The numerical results show that our proposed precoding significantly outperforms quantization-unaware precoding and other previous approaches in terms of the sum rate. The performance loss for our heuristic method compared to quantization-aware precoding is insignificant considering the complexity reduction, which makes the heuristic method feasible for real-time applications. We consider both perfect and imperfect channel state information.

Convex quantization preserves logconcavity

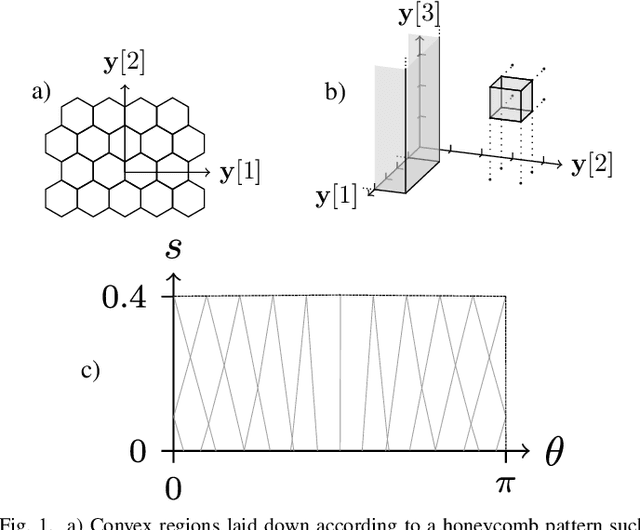
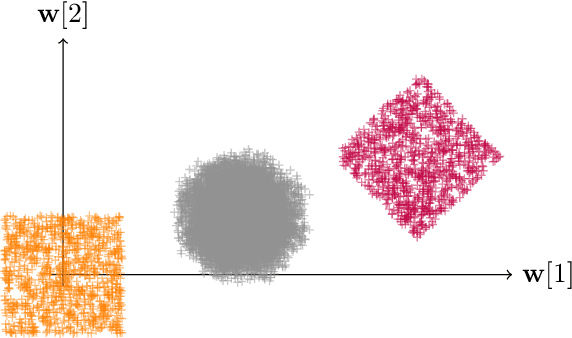
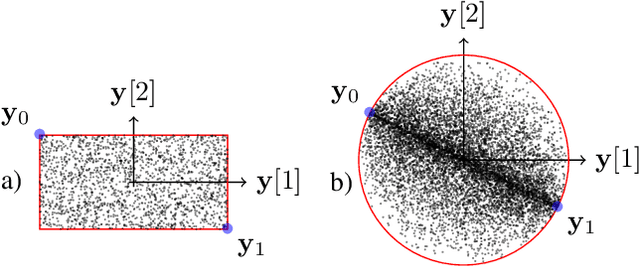
Much like convexity is key to variational optimization, a logconcave distribution is key to amenable statistical inference. Quantization is often disregarded when writing likelihood models: ignoring the limitations of physical detectors. This begs the questions: would including quantization preclude logconcavity, and, are the true data likelihoods logconcave? We show that the same simple assumption that leads to logconcave continuous data likelihoods also leads to logconcave quantized data likelihoods, provided that convex quantization regions are used.

A matrix-inverse-free implementation of the MU-MIMO WMMSE beamforming algorithm

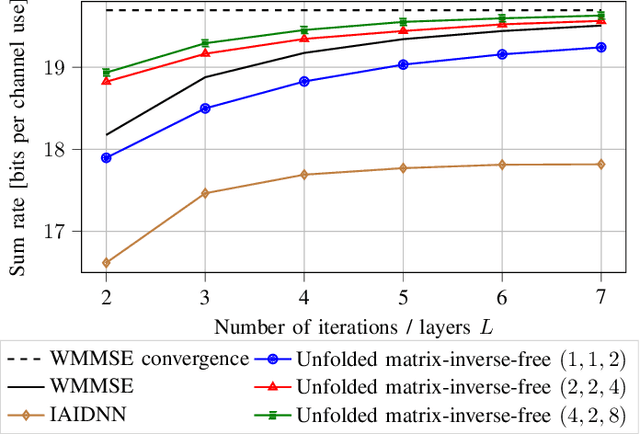
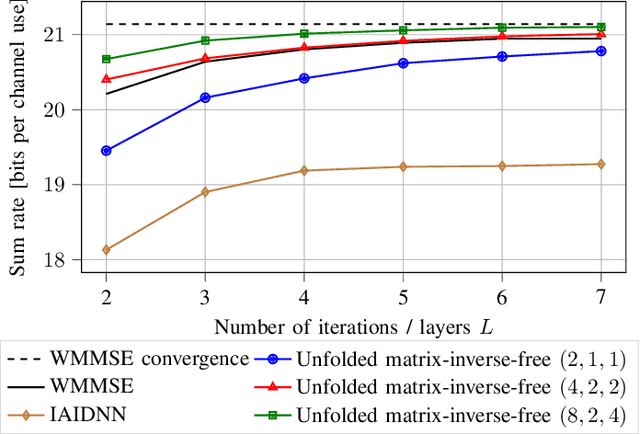
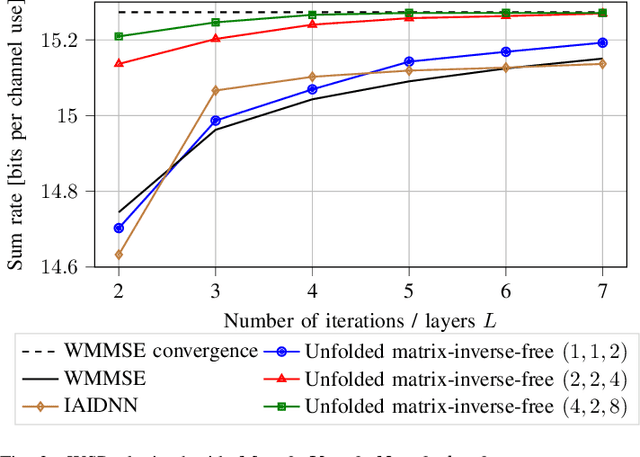
The WMMSE beamforming algorithm is a popular approach to address the NP-hard weighted sum rate (WSR) maximization beamforming problem. Although it efficiently finds a local optimum, it requires matrix inverses, eigendecompositions, and bisection searches, operations that are problematic for real-time implementation. In our previous work, we considered the MU-MISO case and effectively replaced such operations by resorting to a first-order method. Here, we consider the more general and challenging MU-MIMO case. Our earlier approach does not generalize to this scenario and cannot be applied to replace all the hard-to-parallelize operations that appear in the MU-MIMO case. Thus, we propose to leverage a reformulation of the auxiliary WMMSE function given by Hu et al. By applying gradient descent and Schulz iterations, we formulate the first variant of the WMMSE algorithm applicable to the MU-MIMO case that is free from matrix inverses and other serial operations and hence amenable to both real-time implementation and deep unfolding. From a theoretical viewpoint, we establish its convergence to a stationary point of the WSR maximization problem. From a practical viewpoint, we show that in a deep-unfolding-based implementation, the matrix-inverse-free WMMSE algorithm attains, within a fixed number of iterations, a WSR comparable to the original WMMSE algorithm truncated to the same number of iterations, yet with significant implementation advantages in terms of parallelizability and real-time execution.

Inertial Navigation Using an Inertial Sensor Array

We present a comprehensive framework for fusing measurements from multiple and generally placed accelerometers and gyroscopes to perform inertial navigation. Using the angular acceleration provided by the accelerometer array, we show that the numerical integration of the orientation can be done with second-order accuracy, which is more accurate compared to the traditional first-order accuracy that can be achieved when only using the gyroscopes. Since orientation errors are the most significant error source in inertial navigation, improving the orientation estimation reduces the overall navigation error. The practical performance benefit depends on prior knowledge of the inertial sensor array, and therefore we present four different state-space models using different underlying assumptions regarding the orientation modeling. The models are evaluated using a Lie Group Extended Kalman filter through simulations and real-world experiments. We also show how individual accelerometer biases are unobservable and can be replaced by a six-dimensional bias term whose dimension is fixed and independent of the number of accelerometers.

Reinforcement Learning for Efficient and Tuning-Free Link Adaptation

Link adaptation (LA) optimizes the selection of modulation and coding schemes (MCS) for a stochastic wireless channel. The classical outer loop LA (OLLA) tracks the channel's signal-to-noise-and-interference ratio (SINR) based on the observed transmission outcomes. On the other hand, recent Reinforcement learning LA (RLLA) schemes sample the available MCSs to optimize the link performance objective. However, both OLLA and RLLA rely on tuning parameters that are challenging to configure. Further, OLLA optimizes for a target block error rate (BLER) that only indirectly relates to the common throughput-maximization objective, while RLLA does not fully exploit the inter-dependence between the MCSs. In this paper, we propose latent Thompson Sampling for LA (LTSLA), a RLLA scheme that does not require configuration tuning, and which fully exploits MCS inter-dependence for efficient learning. LTSLA models an SINR probability distribution for MCS selection, and refines this distribution through Bayesian updates with the transmission outcomes. LTSLA also automatically adapts to different channel fading profiles by utilizing their respective Doppler estimates. We perform simulation studies of LTSLA along with OLLA and RLLA schemes for frequency selective fading channels. Numerical results demonstrate that LTSLA improves the instantaneous link throughout by up to 50% compared to existing schemes.

Deep unfolding of the weighted MMSE beamforming algorithm

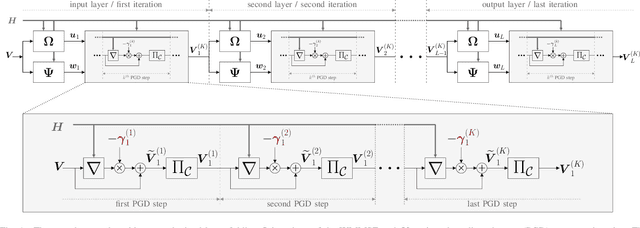
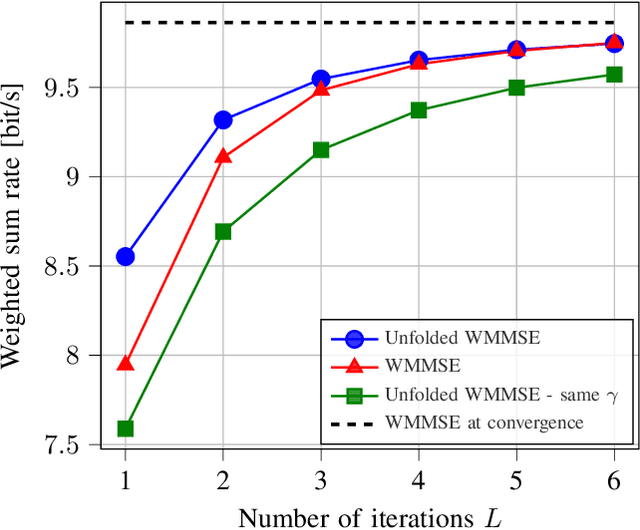
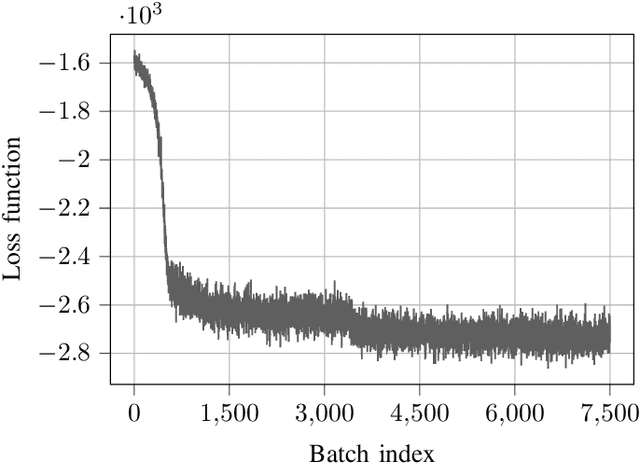
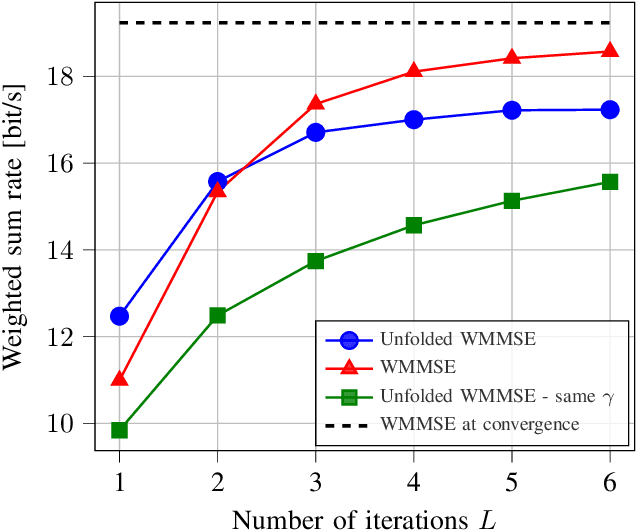
Downlink beamforming is a key technology for cellular networks. However, computing the transmit beamformer that maximizes the weighted sum rate subject to a power constraint is an NP-hard problem. As a result, iterative algorithms that converge to a local optimum are used in practice. Among them, the weighted minimum mean square error (WMMSE) algorithm has gained popularity, but its computational complexity and consequent latency has motivated the need for lower-complexity approximations at the expense of performance. Motivated by the recent success of deep unfolding in the trade-off between complexity and performance, we propose the novel application of deep unfolding to the WMMSE algorithm for a MISO downlink channel. The main idea consists of mapping a fixed number of iterations of the WMMSE algorithm into trainable neural network layers, whose architecture reflects the structure of the original algorithm. With respect to traditional end-to-end learning, deep unfolding naturally incorporates expert knowledge, with the benefits of immediate and well-grounded architecture selection, fewer trainable parameters, and better explainability. However, the formulation of the WMMSE algorithm, as described in Shi et al., is not amenable to be unfolded due to a matrix inversion, an eigendecomposition, and a bisection search performed at each iteration. Therefore, we present an alternative formulation that circumvents these operations by resorting to projected gradient descent. By means of simulations, we show that, in most of the settings, the unfolded WMMSE outperforms or performs equally to the WMMSE for a fixed number of iterations, with the advantage of a lower computational load.

Thompson Sampling for Linearly Constrained Bandits

We address multi-armed bandits (MAB) where the objective is to maximize the cumulative reward under a probabilistic linear constraint. For a few real-world instances of this problem, constrained extensions of the well-known Thompson Sampling (TS) heuristic have recently been proposed. However, finite-time analysis of constrained TS is challenging; as a result, only O(\sqrt{T}) bounds on the cumulative reward loss (i.e., the regret) are available. In this paper, we describe LinConTS, a TS-based algorithm for bandits that place a linear constraint on the probability of earning a reward in every round. We show that for LinConTS, the regret as well as the cumulative constraint violations are upper bounded by O(\log T) for the suboptimal arms. We develop a proof technique that relies on careful analysis of the dual problem and combine it with recent theoretical work on unconstrained TS. Through numerical experiments on two real-world datasets, we demonstrate that LinConTS outperforms an asymptotically optimal upper confidence bound (UCB) scheme in terms of simultaneously minimizing the regret and the violation.