Convex quantization preserves logconcavity
Paper and Code
Jun 11, 2022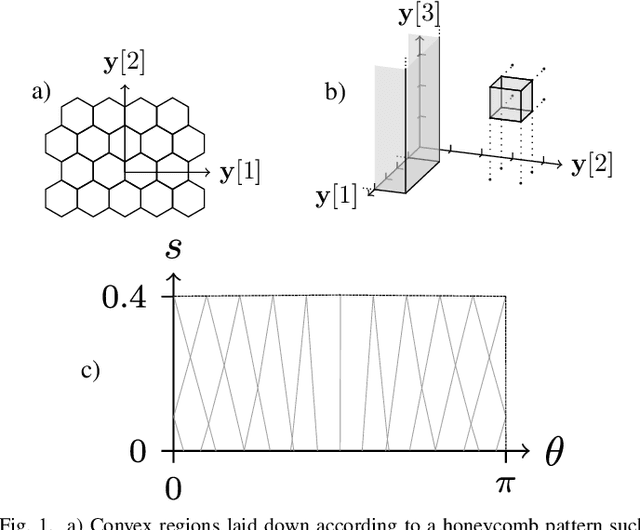
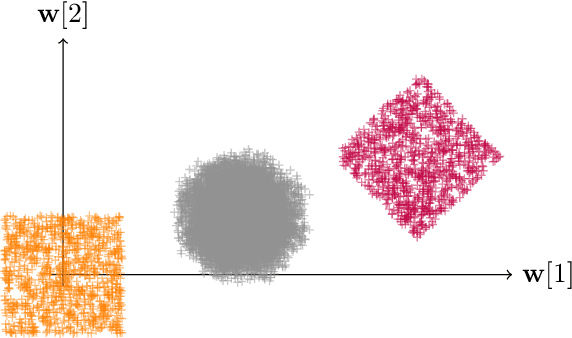
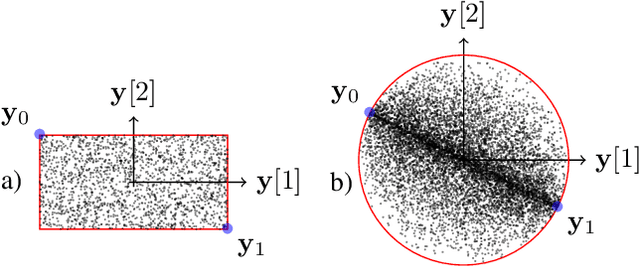
Much like convexity is key to variational optimization, a logconcave distribution is key to amenable statistical inference. Quantization is often disregarded when writing likelihood models: ignoring the limitations of physical detectors. This begs the questions: would including quantization preclude logconcavity, and, are the true data likelihoods logconcave? We show that the same simple assumption that leads to logconcave continuous data likelihoods also leads to logconcave quantized data likelihoods, provided that convex quantization regions are used.
* 5 pages
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge