Self-Supervised Isotropic Superresolution Fetal Brain MRI

Superresolution T2-weighted fetal-brain magnetic-resonance imaging (FBMRI) traditionally relies on the availability of several orthogonal low-resolution series of 2-dimensional thick slices (volumes). In practice, only a few low-resolution volumes are acquired. Thus, optimization-based image-reconstruction methods require strong regularization using hand-crafted regularizers (e.g., TV). Yet, due to in utero fetal motion and the rapidly changing fetal brain anatomy, the acquisition of the high-resolution images that are required to train supervised learning methods is difficult. In this paper, we sidestep this difficulty by providing a proof of concept of a self-supervised single-volume superresolution framework for T2-weighted FBMRI (SAIR). We validate SAIR quantitatively in a motion-free simulated environment. Our results for different noise levels and resolution ratios suggest that SAIR is comparable to multiple-volume superresolution reconstruction methods. We also evaluate SAIR qualitatively on clinical FBMRI data. The results suggest SAIR could be incorporated into current reconstruction pipelines.

Stability of image reconstruction algorithms

Robustness and stability of image reconstruction algorithms have recently come under scrutiny. Their importance to medical imaging cannot be overstated. We review the known results for the topical variational regularization strategies ($\ell_2$ and $\ell_1$ regularization), and present new stability results for $\ell_p$ regularized linear inverse problems for $p\in(1,\infty)$. Our results generalize well to the respective $L_p(\Omega)$ function spaces.

Convex quantization preserves logconcavity

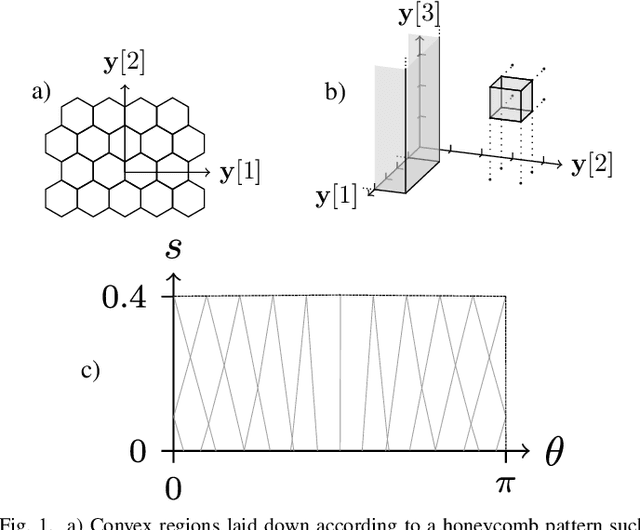
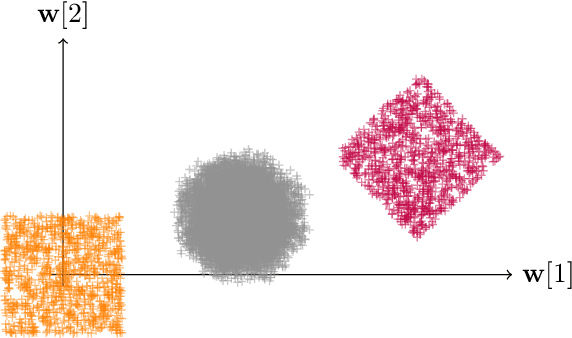
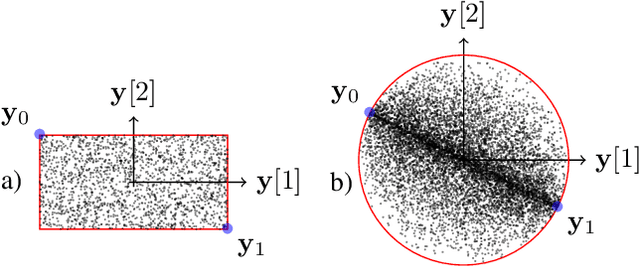
Much like convexity is key to variational optimization, a logconcave distribution is key to amenable statistical inference. Quantization is often disregarded when writing likelihood models: ignoring the limitations of physical detectors. This begs the questions: would including quantization preclude logconcavity, and, are the true data likelihoods logconcave? We show that the same simple assumption that leads to logconcave continuous data likelihoods also leads to logconcave quantized data likelihoods, provided that convex quantization regions are used.

A Statistical Framework to Investigate the Optimality of Neural Networks for Inverse Problems

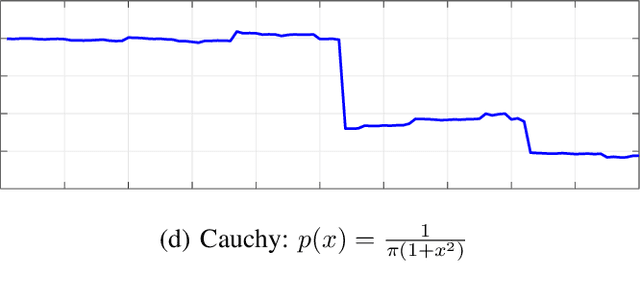
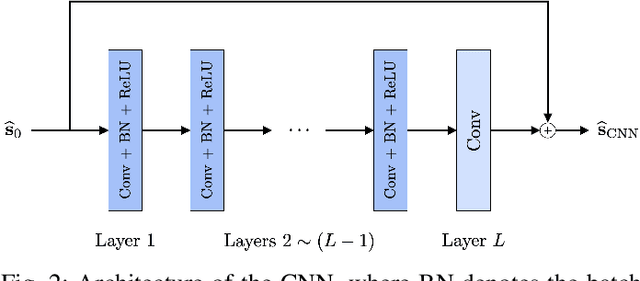
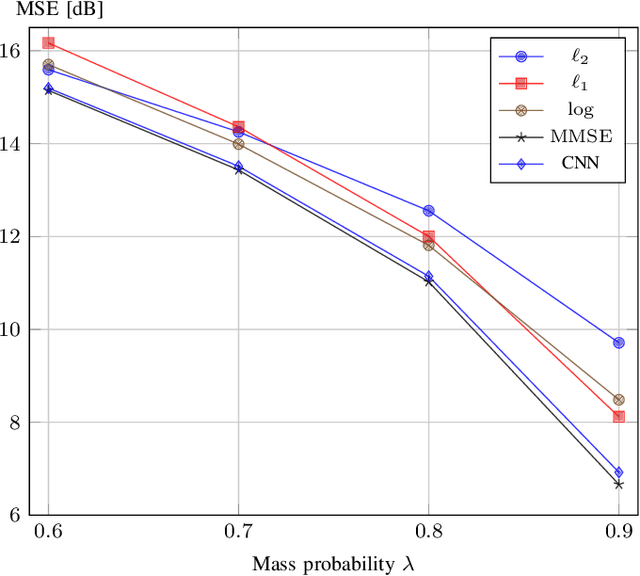
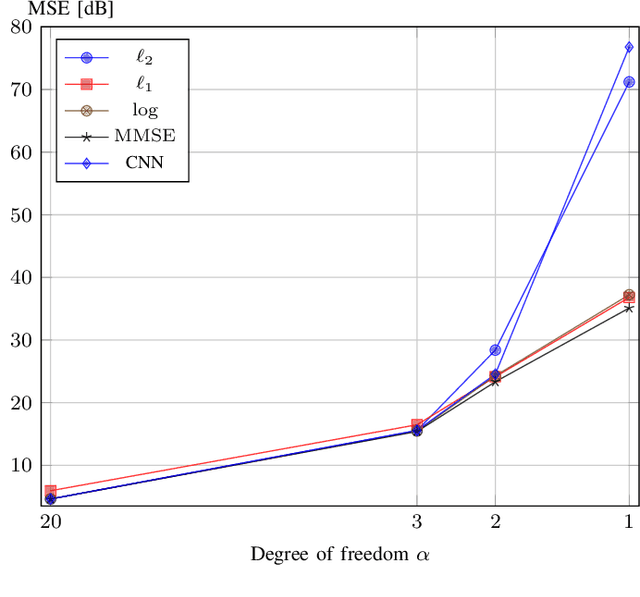
We present a statistical framework to benchmark the performance of neural-network-based reconstruction algorithms for linear inverse problems. The underlying signals in our framework are realizations of sparse stochastic processes and are ideally matched to variational sparsity-promoting techniques, some of which can be reinterpreted as their maximum a posteriori (MAP) estimators. We derive Gibbs sampling schemes to compute the minimum mean square error (MMSE) estimators for processes with Laplace, Student's t and Bernoulli-Laplace innovations. These allow our framework to provide quantitative measures of the degree of optimality (in the mean-square-error sense) for any given reconstruction method. We showcase the use of our framework by benchmarking the performance of CNN architectures for deconvolution and Fourier sampling problems. Our experimental results suggest that while these architectures achieve near-optimal results in many settings, their performance deteriorates severely for signals associated with heavy-tailed distributions.

Optimal transport-based metric for SMLM

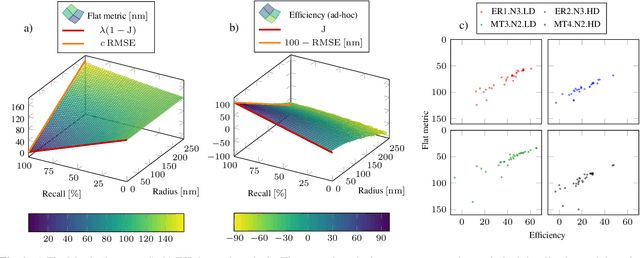
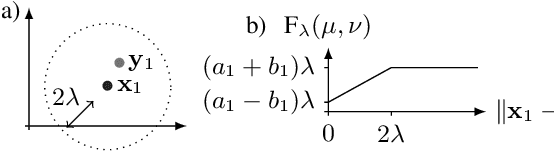
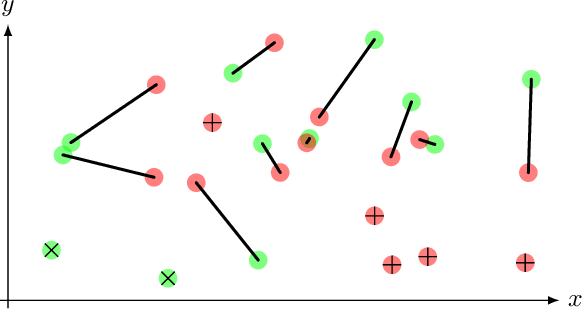
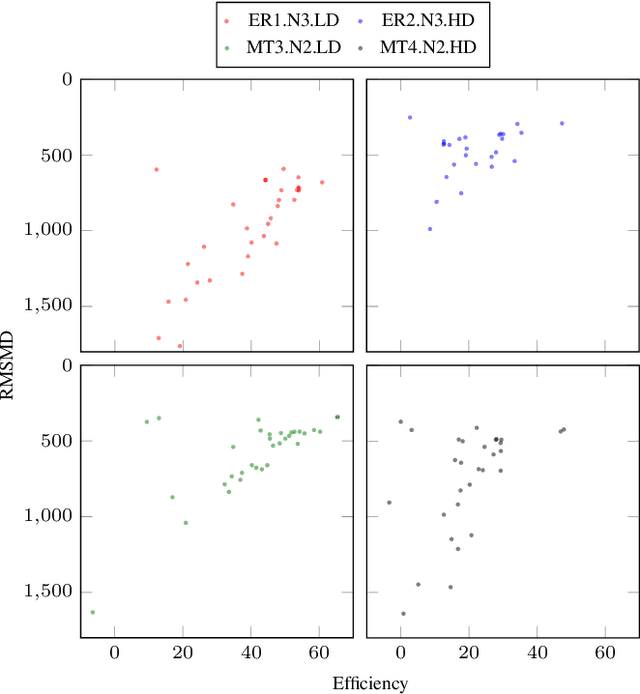
We propose the use of Flat Metric to assess the performance of reconstruction methods for single-molecule localization microscopy (SMLM)in scenarios where the ground-truth is available. Flat Metric is intimately related to the concept of optimal transport between measures of different mass, providing solid mathematical foundations for SMLM evaluation and integrating both localization and detection performance. In this paper, we introduce the foundations of Flat Metric and validate this measure by applying it to controlled synthetic examples and to data from the SMLM 2016 Challenge.