A Statistical Framework to Investigate the Optimality of Neural Networks for Inverse Problems

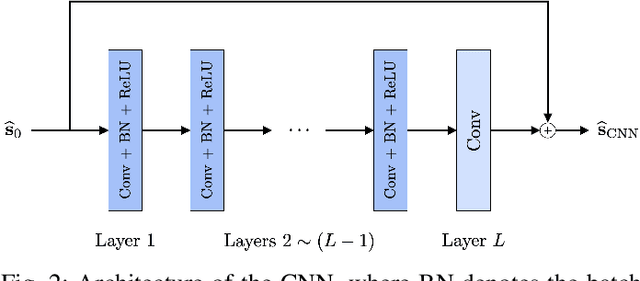
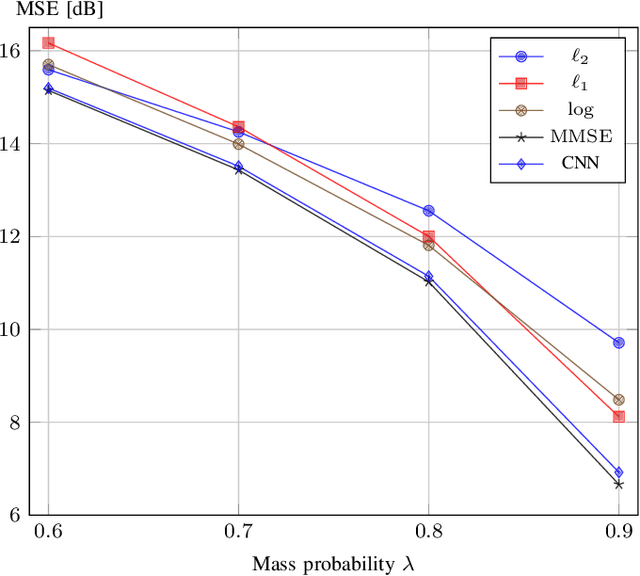
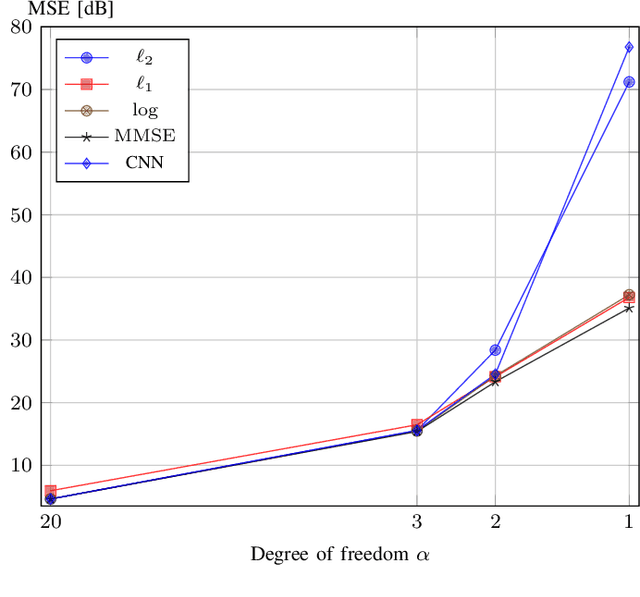
We present a statistical framework to benchmark the performance of neural-network-based reconstruction algorithms for linear inverse problems. The underlying signals in our framework are realizations of sparse stochastic processes and are ideally matched to variational sparsity-promoting techniques, some of which can be reinterpreted as their maximum a posteriori (MAP) estimators. We derive Gibbs sampling schemes to compute the minimum mean square error (MMSE) estimators for processes with Laplace, Student's t and Bernoulli-Laplace innovations. These allow our framework to provide quantitative measures of the degree of optimality (in the mean-square-error sense) for any given reconstruction method. We showcase the use of our framework by benchmarking the performance of CNN architectures for deconvolution and Fourier sampling problems. Our experimental results suggest that while these architectures achieve near-optimal results in many settings, their performance deteriorates severely for signals associated with heavy-tailed distributions.