Multivariate Fields of Experts

We introduce the multivariate fields of experts, a new framework for the learning of image priors. Our model generalizes existing fields of experts methods by incorporating multivariate potential functions constructed via Moreau envelopes of the $\ell_\infty$-norm. We demonstrate the effectiveness of our proposal across a range of inverse problems that include image denoising, deblurring, compressed-sensing magnetic-resonance imaging, and computed tomography. The proposed approach outperforms comparable univariate models and achieves performance close to that of deep-learning-based regularizers while being significantly faster, requiring fewer parameters, and being trained on substantially fewer data. In addition, our model retains a relatively high level of interpretability due to its structured design.

The Gaussian Latent Machine: Efficient Prior and Posterior Sampling for Inverse Problems

We consider the problem of sampling from a product-of-experts-type model that encompasses many standard prior and posterior distributions commonly found in Bayesian imaging. We show that this model can be easily lifted into a novel latent variable model, which we refer to as a Gaussian latent machine. This leads to a general sampling approach that unifies and generalizes many existing sampling algorithms in the literature. Most notably, it yields a highly efficient and effective two-block Gibbs sampling approach in the general case, while also specializing to direct sampling algorithms in particular cases. Finally, we present detailed numerical experiments that demonstrate the efficiency and effectiveness of our proposed sampling approach across a wide range of prior and posterior sampling problems from Bayesian imaging.

Generalized Ray Tracing with Basis functions for Tomographic Projections

This work aims at the precise and efficient computation of the x-ray projection of an image represented by a linear combination of general shifted basis functions that typically overlap. We achieve this with a suitable adaptation of ray tracing, which is one of the most efficient methods to compute line integrals. In our work, the cases in which the image is expressed as a spline are of particular relevance. The proposed implementation is applicable to any projection geometry as it computes the forward and backward operators over a collection of arbitrary lines. We validate our work with experiments in the context of inverse problems for image reconstruction and maximize the image quality for a given resolution of the reconstruction grid.

Universal Architectures for the Learning of Polyhedral Norms and Convex Regularization Functionals

This paper addresses the task of learning convex regularizers to guide the reconstruction of images from limited data. By imposing that the reconstruction be amplitude-equivariant, we narrow down the class of admissible functionals to those that can be expressed as a power of a seminorm. We then show that such functionals can be approximated to arbitrary precision with the help of polyhedral norms. In particular, we identify two dual parameterizations of such systems: (i) a synthesis form with an $\ell_1$-penalty that involves some learnable dictionary; and (ii) an analysis form with an $\ell_\infty$-penalty that involves a trainable regularization operator. After having provided geometric insights and proved that the two forms are universal, we propose an implementation that relies on a specific architecture (tight frame with a weighted $\ell_1$ penalty) that is easy to train. We illustrate its use for denoising and the reconstruction of biomedical images. We find that the proposed framework outperforms the sparsity-based methods of compressed sensing, while it offers essentially the same convergence and robustness guarantees.

DEALing with Image Reconstruction: Deep Attentive Least Squares

State-of-the-art image reconstruction often relies on complex, highly parameterized deep architectures. We propose an alternative: a data-driven reconstruction method inspired by the classic Tikhonov regularization. Our approach iteratively refines intermediate reconstructions by solving a sequence of quadratic problems. These updates have two key components: (i) learned filters to extract salient image features, and (ii) an attention mechanism that locally adjusts the penalty of filter responses. Our method achieves performance on par with leading plug-and-play and learned regularizer approaches while offering interpretability, robustness, and convergent behavior. In effect, we bridge traditional regularization and deep learning with a principled reconstruction approach.

Comparison of 2D Regular Lattices for the CPWL Approximation of Functions

We investigate the approximation error of functions with continuous and piecewise-linear (CPWL) representations. We focus on the CPWL search spaces generated by translates of box splines on two-dimensional regular lattices. We compute the approximation error in terms of the stepsize and angles that define the lattice. Our results show that hexagonal lattices are optimal, in the sense that they minimize the asymptotic approximation error.

Learning of Patch-Based Smooth-Plus-Sparse Models for Image Reconstruction

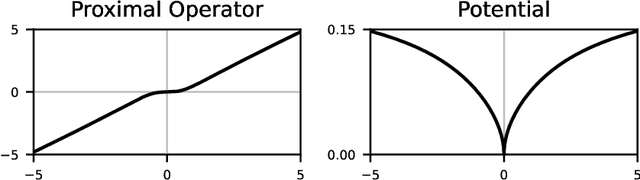
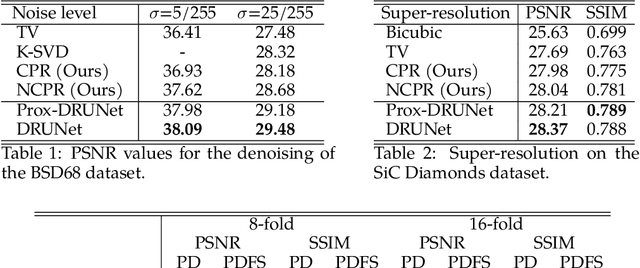
We aim at the solution of inverse problems in imaging, by combining a penalized sparse representation of image patches with an unconstrained smooth one. This allows for a straightforward interpretation of the reconstruction. We formulate the optimization as a bilevel problem. The inner problem deploys classical algorithms while the outer problem optimizes the dictionary and the regularizer parameters through supervised learning. The process is carried out via implicit differentiation and gradient-based optimization. We evaluate our method for denoising, super-resolution, and compressed-sensing magnetic-resonance imaging. We compare it to other classical models as well as deep-learning-based methods and show that it always outperforms the former and also the latter in some instances.

Controlled Learning of Pointwise Nonlinearities in Neural-Network-Like Architectures

We present a general variational framework for the training of freeform nonlinearities in layered computational architectures subject to some slope constraints. The regularization that we add to the traditional training loss penalizes the second-order total variation of each trainable activation. The slope constraints allow us to impose properties such as 1-Lipschitz stability, firm non-expansiveness, and monotonicity/invertibility. These properties are crucial to ensure the proper functioning of certain classes of signal-processing algorithms (e.g., plug-and-play schemes, unrolled proximal gradient, invertible flows). We prove that the global optimum of the stated constrained-optimization problem is achieved with nonlinearities that are adaptive nonuniform linear splines. We then show how to solve the resulting function-optimization problem numerically by representing the nonlinearities in a suitable (nonuniform) B-spline basis. Finally, we illustrate the use of our framework with the data-driven design of (weakly) convex regularizers for the denoising of images and the resolution of inverse problems.

Parseval Convolution Operators and Neural Networks

We first establish a kernel theorem that characterizes all linear shift-invariant (LSI) operators acting on discrete multicomponent signals. This result naturally leads to the identification of the Parseval convolution operators as the class of energy-preserving filterbanks. We then present a constructive approach for the design/specification of such filterbanks via the chaining of elementary Parseval modules, each of which being parameterized by an orthogonal matrix or a 1-tight frame. Our analysis is complemented with explicit formulas for the Lipschitz constant of all the components of a convolutional neural network (CNN), which gives us a handle on their stability. Finally, we demonstrate the usage of those tools with the design of a CNN-based algorithm for the iterative reconstruction of biomedical images. Our algorithm falls within the plug-and-play framework for the resolution of inverse problems. It yields better-quality results than the sparsity-based methods used in compressed sensing, while offering essentially the same convergence and robustness guarantees.

Self-Calibrated Variance-Stabilizing Transformations for Real-World Image Denoising

Supervised deep learning has become the method of choice for image denoising. It involves the training of neural networks on large datasets composed of pairs of noisy and clean images. However, the necessity of training data that are specific to the targeted application constrains the widespread use of denoising networks. Recently, several approaches have been developed to overcome this difficulty by whether artificially generating realistic clean/noisy image pairs, or training exclusively on noisy images. In this paper, we show that, contrary to popular belief, denoising networks specialized in the removal of Gaussian noise can be efficiently leveraged in favor of real-world image denoising, even without additional training. For this to happen, an appropriate variance-stabilizing transform (VST) has to be applied beforehand. We propose an algorithm termed Noise2VST for the learning of such a model-free VST. Our approach requires only the input noisy image and an off-the-shelf Gaussian denoiser. We demonstrate through extensive experiments the efficiency and superiority of Noise2VST in comparison to existing methods trained in the absence of specific clean/noisy pairs.