Multivariate Fields of Experts

We introduce the multivariate fields of experts, a new framework for the learning of image priors. Our model generalizes existing fields of experts methods by incorporating multivariate potential functions constructed via Moreau envelopes of the $\ell_\infty$-norm. We demonstrate the effectiveness of our proposal across a range of inverse problems that include image denoising, deblurring, compressed-sensing magnetic-resonance imaging, and computed tomography. The proposed approach outperforms comparable univariate models and achieves performance close to that of deep-learning-based regularizers while being significantly faster, requiring fewer parameters, and being trained on substantially fewer data. In addition, our model retains a relatively high level of interpretability due to its structured design.

Universal Architectures for the Learning of Polyhedral Norms and Convex Regularization Functionals

This paper addresses the task of learning convex regularizers to guide the reconstruction of images from limited data. By imposing that the reconstruction be amplitude-equivariant, we narrow down the class of admissible functionals to those that can be expressed as a power of a seminorm. We then show that such functionals can be approximated to arbitrary precision with the help of polyhedral norms. In particular, we identify two dual parameterizations of such systems: (i) a synthesis form with an $\ell_1$-penalty that involves some learnable dictionary; and (ii) an analysis form with an $\ell_\infty$-penalty that involves a trainable regularization operator. After having provided geometric insights and proved that the two forms are universal, we propose an implementation that relies on a specific architecture (tight frame with a weighted $\ell_1$ penalty) that is easy to train. We illustrate its use for denoising and the reconstruction of biomedical images. We find that the proposed framework outperforms the sparsity-based methods of compressed sensing, while it offers essentially the same convergence and robustness guarantees.

Learning of Patch-Based Smooth-Plus-Sparse Models for Image Reconstruction

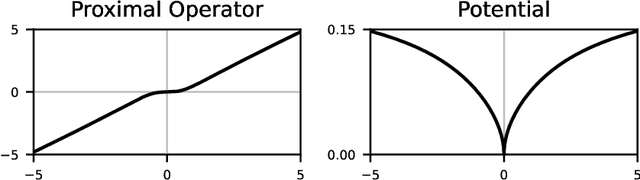
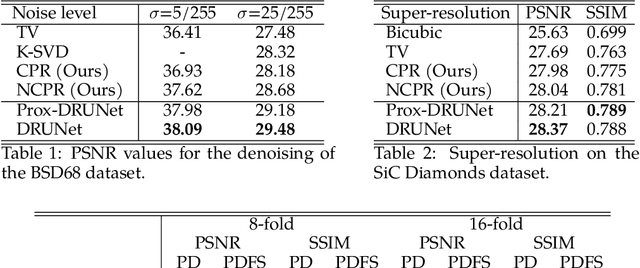
We aim at the solution of inverse problems in imaging, by combining a penalized sparse representation of image patches with an unconstrained smooth one. This allows for a straightforward interpretation of the reconstruction. We formulate the optimization as a bilevel problem. The inner problem deploys classical algorithms while the outer problem optimizes the dictionary and the regularizer parameters through supervised learning. The process is carried out via implicit differentiation and gradient-based optimization. We evaluate our method for denoising, super-resolution, and compressed-sensing magnetic-resonance imaging. We compare it to other classical models as well as deep-learning-based methods and show that it always outperforms the former and also the latter in some instances.

Controlled Learning of Pointwise Nonlinearities in Neural-Network-Like Architectures

We present a general variational framework for the training of freeform nonlinearities in layered computational architectures subject to some slope constraints. The regularization that we add to the traditional training loss penalizes the second-order total variation of each trainable activation. The slope constraints allow us to impose properties such as 1-Lipschitz stability, firm non-expansiveness, and monotonicity/invertibility. These properties are crucial to ensure the proper functioning of certain classes of signal-processing algorithms (e.g., plug-and-play schemes, unrolled proximal gradient, invertible flows). We prove that the global optimum of the stated constrained-optimization problem is achieved with nonlinearities that are adaptive nonuniform linear splines. We then show how to solve the resulting function-optimization problem numerically by representing the nonlinearities in a suitable (nonuniform) B-spline basis. Finally, we illustrate the use of our framework with the data-driven design of (weakly) convex regularizers for the denoising of images and the resolution of inverse problems.

Parseval Convolution Operators and Neural Networks

We first establish a kernel theorem that characterizes all linear shift-invariant (LSI) operators acting on discrete multicomponent signals. This result naturally leads to the identification of the Parseval convolution operators as the class of energy-preserving filterbanks. We then present a constructive approach for the design/specification of such filterbanks via the chaining of elementary Parseval modules, each of which being parameterized by an orthogonal matrix or a 1-tight frame. Our analysis is complemented with explicit formulas for the Lipschitz constant of all the components of a convolutional neural network (CNN), which gives us a handle on their stability. Finally, we demonstrate the usage of those tools with the design of a CNN-based algorithm for the iterative reconstruction of biomedical images. Our algorithm falls within the plug-and-play framework for the resolution of inverse problems. It yields better-quality results than the sparsity-based methods used in compressed sensing, while offering essentially the same convergence and robustness guarantees.

A Neural-Network-Based Convex Regularizer for Image Reconstruction

The emergence of deep-learning-based methods for solving inverse problems has enabled a significant increase in reconstruction quality. Unfortunately, these new methods often lack reliability and explainability, and there is a growing interest to address these shortcomings while retaining the performance. In this work, this problem is tackled by revisiting regularizers that are the sum of convex-ridge functions. The gradient of such regularizers is parametrized by a neural network that has a single hidden layer with increasing and learnable activation functions. This neural network is trained within a few minutes as a multi-step Gaussian denoiser. The numerical experiments for denoising, CT, and MRI reconstruction show improvements over methods that offer similar reliability guarantees.

Improving Lipschitz-Constrained Neural Networks by Learning Activation Functions

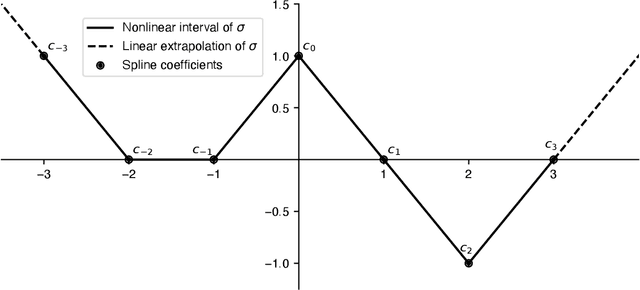
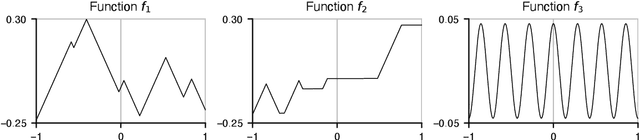
Lipschitz-constrained neural networks have several advantages compared to unconstrained ones and can be applied to various different problems. Consequently, they have recently attracted considerable attention in the deep learning community. Unfortunately, it has been shown both theoretically and empirically that networks with ReLU activation functions perform poorly under such constraints. On the contrary, neural networks with learnable 1-Lipschitz linear splines are known to be more expressive in theory. In this paper, we show that such networks are solutions of a functional optimization problem with second-order total-variation regularization. Further, we propose an efficient method to train such 1-Lipschitz deep spline neural networks. Our numerical experiments for a variety of tasks show that our trained networks match or outperform networks with activation functions specifically tailored towards Lipschitz-constrained architectures.