Controlled Learning of Pointwise Nonlinearities in Neural-Network-Like Architectures

We present a general variational framework for the training of freeform nonlinearities in layered computational architectures subject to some slope constraints. The regularization that we add to the traditional training loss penalizes the second-order total variation of each trainable activation. The slope constraints allow us to impose properties such as 1-Lipschitz stability, firm non-expansiveness, and monotonicity/invertibility. These properties are crucial to ensure the proper functioning of certain classes of signal-processing algorithms (e.g., plug-and-play schemes, unrolled proximal gradient, invertible flows). We prove that the global optimum of the stated constrained-optimization problem is achieved with nonlinearities that are adaptive nonuniform linear splines. We then show how to solve the resulting function-optimization problem numerically by representing the nonlinearities in a suitable (nonuniform) B-spline basis. Finally, we illustrate the use of our framework with the data-driven design of (weakly) convex regularizers for the denoising of images and the resolution of inverse problems.

Learning Weakly Convex Regularizers for Convergent Image-Reconstruction Algorithms

We propose to learn non-convex regularizers with a prescribed upper bound on their weak-convexity modulus. Such regularizers give rise to variational denoisers that minimize a convex energy. They rely on few parameters (less than 15,000) and offer a signal-processing interpretation as they mimic handcrafted sparsity-promoting regularizers. Through numerical experiments, we show that such denoisers outperform convex-regularization methods as well as the popular BM3D denoiser. Additionally, the learned regularizer can be deployed to solve inverse problems with iterative schemes that provably converge. For both CT and MRI reconstruction, the regularizer generalizes well and offers an excellent tradeoff between performance, number of parameters, guarantees, and interpretability when compared to other data-driven approaches.

A Neural-Network-Based Convex Regularizer for Image Reconstruction

The emergence of deep-learning-based methods for solving inverse problems has enabled a significant increase in reconstruction quality. Unfortunately, these new methods often lack reliability and explainability, and there is a growing interest to address these shortcomings while retaining the performance. In this work, this problem is tackled by revisiting regularizers that are the sum of convex-ridge functions. The gradient of such regularizers is parametrized by a neural network that has a single hidden layer with increasing and learnable activation functions. This neural network is trained within a few minutes as a multi-step Gaussian denoiser. The numerical experiments for denoising, CT, and MRI reconstruction show improvements over methods that offer similar reliability guarantees.

Improving Lipschitz-Constrained Neural Networks by Learning Activation Functions

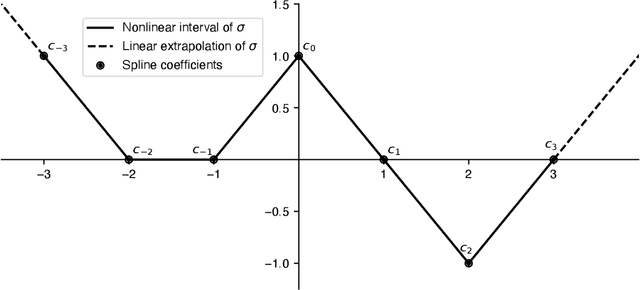
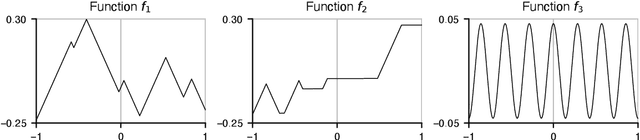
Lipschitz-constrained neural networks have several advantages compared to unconstrained ones and can be applied to various different problems. Consequently, they have recently attracted considerable attention in the deep learning community. Unfortunately, it has been shown both theoretically and empirically that networks with ReLU activation functions perform poorly under such constraints. On the contrary, neural networks with learnable 1-Lipschitz linear splines are known to be more expressive in theory. In this paper, we show that such networks are solutions of a functional optimization problem with second-order total-variation regularization. Further, we propose an efficient method to train such 1-Lipschitz deep spline neural networks. Our numerical experiments for a variety of tasks show that our trained networks match or outperform networks with activation functions specifically tailored towards Lipschitz-constrained architectures.

Delaunay-Triangulation-Based Learning with Hessian Total-Variation Regularization

Regression is one of the core problems tackled in supervised learning. Rectified linear unit (ReLU) neural networks generate continuous and piecewise-linear (CPWL) mappings and are the state-of-the-art approach for solving regression problems. In this paper, we propose an alternative method that leverages the expressivity of CPWL functions. In contrast to deep neural networks, our CPWL parameterization guarantees stability and is interpretable. Our approach relies on the partitioning of the domain of the CPWL function by a Delaunay triangulation. The function values at the vertices of the triangulation are our learnable parameters and identify the CPWL function uniquely. Formulating the learning scheme as a variational problem, we use the Hessian total variation (HTV) as regularizer to favor CPWL functions with few affine pieces. In this way, we control the complexity of our model through a single hyperparameter. By developing a computational framework to compute the HTV of any CPWL function parameterized by a triangulation, we discretize the learning problem as the generalized least absolute shrinkage and selection operator (LASSO). Our experiments validate the usage of our method in low-dimensional scenarios.

The Role of Depth, Width, and Activation Complexity in the Number of Linear Regions of Neural Networks

Many feedforward neural networks generate continuous and piecewise-linear (CPWL) mappings. Specifically, they partition the input domain into regions on which the mapping is an affine function. The number of these so-called linear regions offers a natural metric to characterize the expressiveness of CPWL mappings. Although the precise determination of this quantity is often out of reach, bounds have been proposed for specific architectures, including the well-known ReLU and Maxout networks. In this work, we propose a more general perspective and provide precise bounds on the maximal number of linear regions of CPWL networks based on three sources of expressiveness: depth, width, and activation complexity. Our estimates rely on the combinatorial structure of convex partitions and highlight the distinctive role of depth which, on its own, is able to exponentially increase the number of regions. We then introduce a complementary stochastic framework to estimate the average number of linear regions produced by a CPWL network architecture. Under reasonable assumptions, the expected density of linear regions along any 1D path is bounded by the product of depth, width, and a measure of activation complexity (up to a scaling factor). This yields an identical role to the three sources of expressiveness: no exponential growth with depth is observed anymore.

Approximation of Lipschitz Functions using Deep Spline Neural Networks

Lipschitz-constrained neural networks have many applications in machine learning. Since designing and training expressive Lipschitz-constrained networks is very challenging, there is a need for improved methods and a better theoretical understanding. Unfortunately, it turns out that ReLU networks have provable disadvantages in this setting. Hence, we propose to use learnable spline activation functions with at least 3 linear regions instead. We prove that this choice is optimal among all component-wise $1$-Lipschitz activation functions in the sense that no other weight constrained architecture can approximate a larger class of functions. Additionally, this choice is at least as expressive as the recently introduced non component-wise Groupsort activation function for spectral-norm-constrained weights. Previously published numerical results support our theoretical findings.