Random ReLU Neural Networks as Non-Gaussian Processes

We consider a large class of shallow neural networks with randomly initialized parameters and rectified linear unit activation functions. We prove that these random neural networks are well-defined non-Gaussian processes. As a by-product, we demonstrate that these networks are solutions to stochastic differential equations driven by impulsive white noise (combinations of random Dirac measures). These processes are parameterized by the law of the weights and biases as well as the density of activation thresholds in each bounded region of the input domain. We prove that these processes are isotropic and wide-sense self-similar with Hurst exponent $3/2$. We also derive a remarkably simple closed-form expression for their autocovariance function. Our results are fundamentally different from prior work in that we consider a non-asymptotic viewpoint: The number of neurons in each bounded region of the input domain (i.e., the width) is itself a random variable with a Poisson law with mean proportional to the density parameter. Finally, we show that, under suitable hypotheses, as the expected width tends to infinity, these processes can converge in law not only to Gaussian processes, but also to non-Gaussian processes depending on the law of the weights. Our asymptotic results provide a new take on several classical results (wide networks converge to Gaussian processes) as well as some new ones (wide networks can converge to non-Gaussian processes).

A Neural-Network-Based Convex Regularizer for Image Reconstruction

The emergence of deep-learning-based methods for solving inverse problems has enabled a significant increase in reconstruction quality. Unfortunately, these new methods often lack reliability and explainability, and there is a growing interest to address these shortcomings while retaining the performance. In this work, this problem is tackled by revisiting regularizers that are the sum of convex-ridge functions. The gradient of such regularizers is parametrized by a neural network that has a single hidden layer with increasing and learnable activation functions. This neural network is trained within a few minutes as a multi-step Gaussian denoiser. The numerical experiments for denoising, CT, and MRI reconstruction show improvements over methods that offer similar reliability guarantees.

Improving Lipschitz-Constrained Neural Networks by Learning Activation Functions

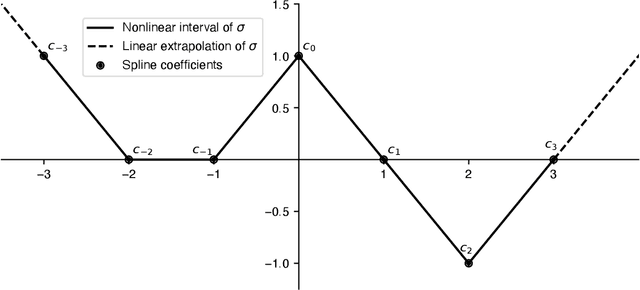
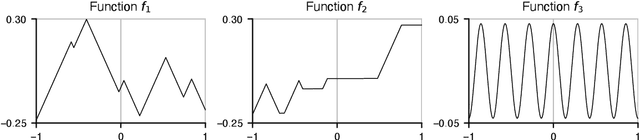
Lipschitz-constrained neural networks have several advantages compared to unconstrained ones and can be applied to various different problems. Consequently, they have recently attracted considerable attention in the deep learning community. Unfortunately, it has been shown both theoretically and empirically that networks with ReLU activation functions perform poorly under such constraints. On the contrary, neural networks with learnable 1-Lipschitz linear splines are known to be more expressive in theory. In this paper, we show that such networks are solutions of a functional optimization problem with second-order total-variation regularization. Further, we propose an efficient method to train such 1-Lipschitz deep spline neural networks. Our numerical experiments for a variety of tasks show that our trained networks match or outperform networks with activation functions specifically tailored towards Lipschitz-constrained architectures.

Approximation of Lipschitz Functions using Deep Spline Neural Networks

Lipschitz-constrained neural networks have many applications in machine learning. Since designing and training expressive Lipschitz-constrained networks is very challenging, there is a need for improved methods and a better theoretical understanding. Unfortunately, it turns out that ReLU networks have provable disadvantages in this setting. Hence, we propose to use learnable spline activation functions with at least 3 linear regions instead. We prove that this choice is optimal among all component-wise $1$-Lipschitz activation functions in the sense that no other weight constrained architecture can approximate a larger class of functions. Additionally, this choice is at least as expressive as the recently introduced non component-wise Groupsort activation function for spectral-norm-constrained weights. Previously published numerical results support our theoretical findings.

Bayesian Inversion for Nonlinear Imaging Models using Deep Generative Priors

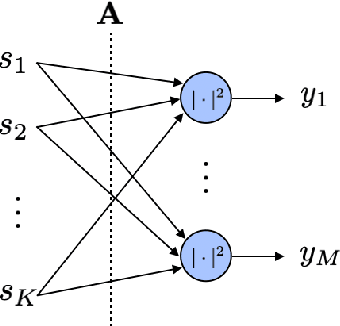
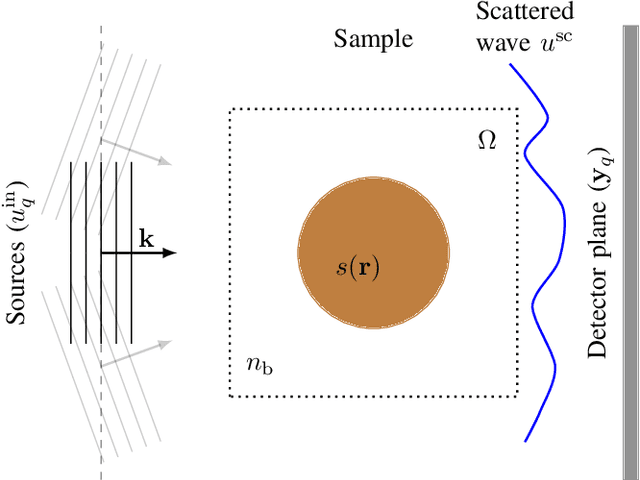
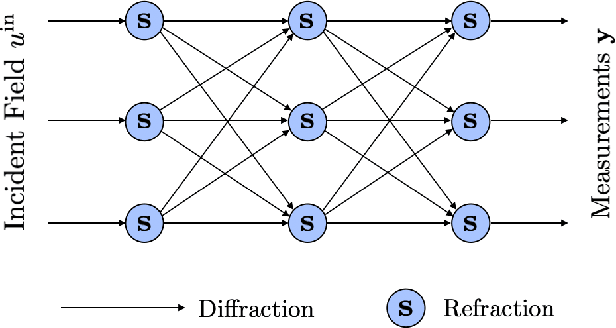
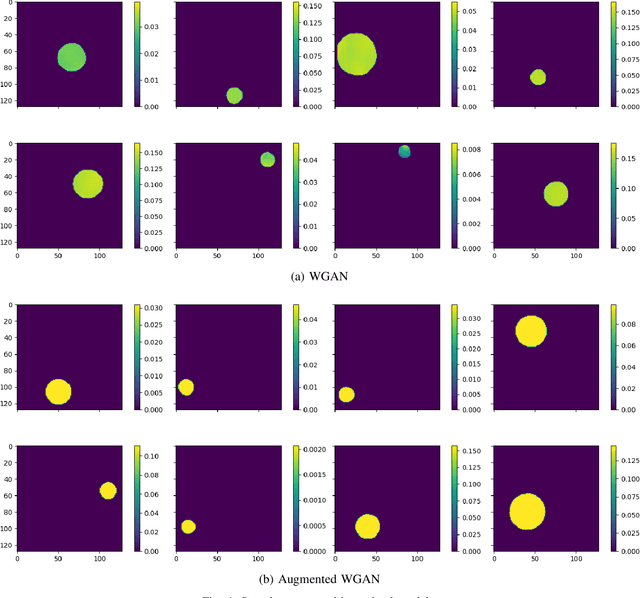
Most modern imaging systems involve a computational reconstruction pipeline to infer the image of interest from acquired measurements. The Bayesian reconstruction framework relies on the characterization of the posterior distribution, which depends on a model of the imaging system and prior knowledge on the image, for solving such inverse problems. Here, the choice of the prior distribution is critical for obtaining high-quality estimates. In this work, we use deep generative models to represent the prior distribution. We develop a posterior sampling scheme for the class of nonlinear inverse problems where the forward model has a neural-network-like structure. This class includes most existing imaging modalities. We introduce the notion of augmented generative models in order to suitably handle quantitative image recovery. We illustrate the advantages of our framework by applying it to two nonlinear imaging modalities-phase retrieval and optical diffraction tomography.

A Statistical Framework to Investigate the Optimality of Neural Networks for Inverse Problems

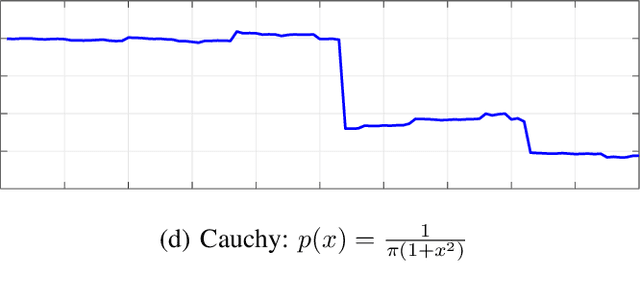
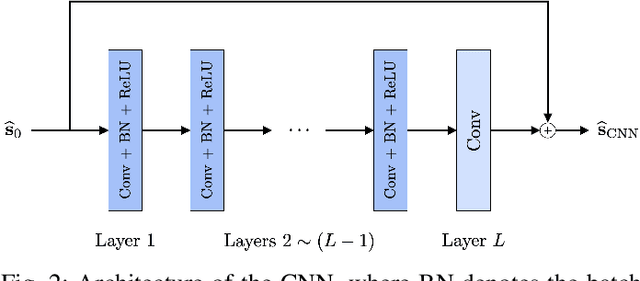
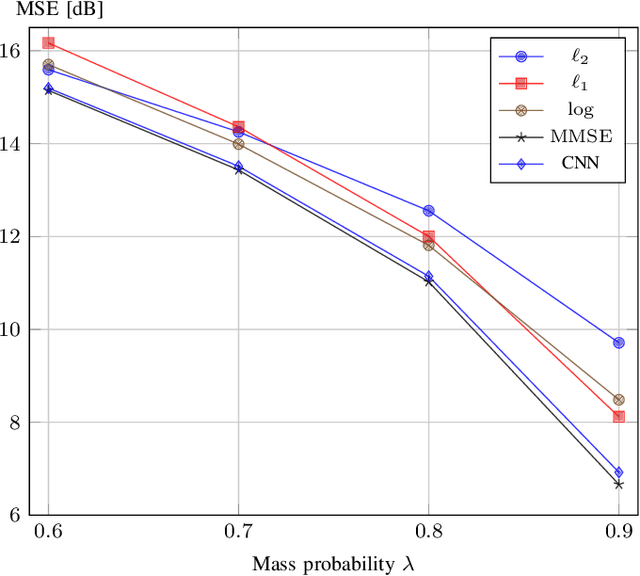
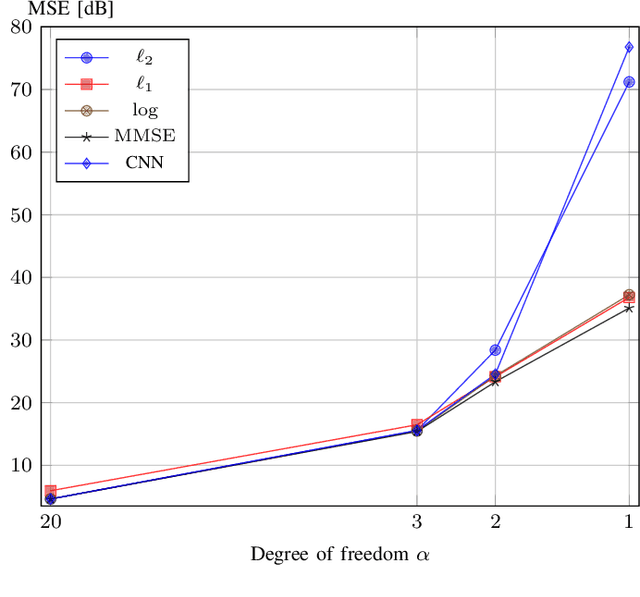
We present a statistical framework to benchmark the performance of neural-network-based reconstruction algorithms for linear inverse problems. The underlying signals in our framework are realizations of sparse stochastic processes and are ideally matched to variational sparsity-promoting techniques, some of which can be reinterpreted as their maximum a posteriori (MAP) estimators. We derive Gibbs sampling schemes to compute the minimum mean square error (MMSE) estimators for processes with Laplace, Student's t and Bernoulli-Laplace innovations. These allow our framework to provide quantitative measures of the degree of optimality (in the mean-square-error sense) for any given reconstruction method. We showcase the use of our framework by benchmarking the performance of CNN architectures for deconvolution and Fourier sampling problems. Our experimental results suggest that while these architectures achieve near-optimal results in many settings, their performance deteriorates severely for signals associated with heavy-tailed distributions.