Bayesian Inversion for Nonlinear Imaging Models using Deep Generative Priors

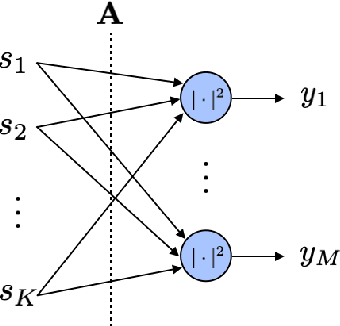
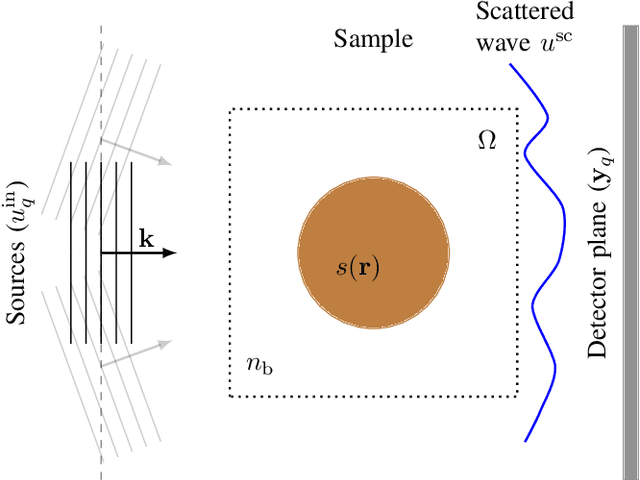
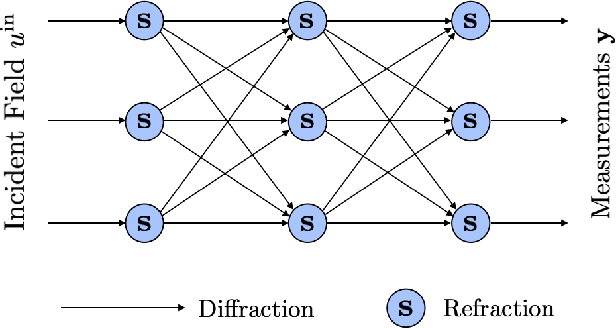
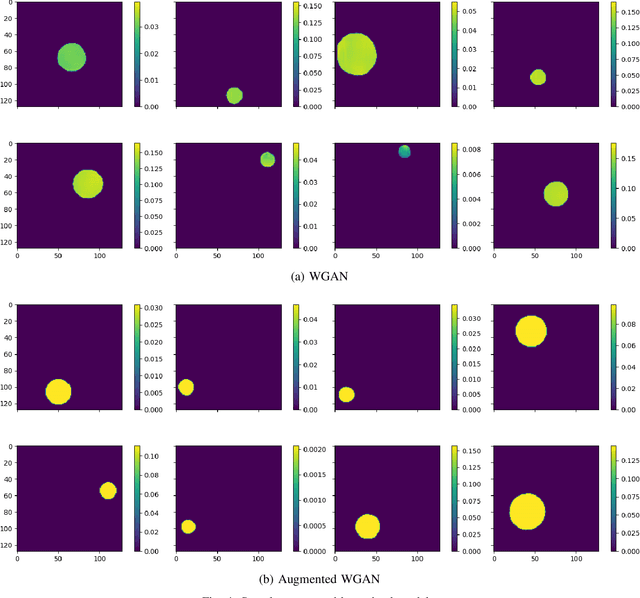
Most modern imaging systems involve a computational reconstruction pipeline to infer the image of interest from acquired measurements. The Bayesian reconstruction framework relies on the characterization of the posterior distribution, which depends on a model of the imaging system and prior knowledge on the image, for solving such inverse problems. Here, the choice of the prior distribution is critical for obtaining high-quality estimates. In this work, we use deep generative models to represent the prior distribution. We develop a posterior sampling scheme for the class of nonlinear inverse problems where the forward model has a neural-network-like structure. This class includes most existing imaging modalities. We introduce the notion of augmented generative models in order to suitably handle quantitative image recovery. We illustrate the advantages of our framework by applying it to two nonlinear imaging modalities-phase retrieval and optical diffraction tomography.