A Mini-Batch Quasi-Newton Proximal Method for Constrained Total-Variation Nonlinear Image Reconstruction

Over the years, computational imaging with accurate nonlinear physical models has drawn considerable interest due to its ability to achieve high-quality reconstructions. However, such nonlinear models are computationally demanding. A popular choice for solving the corresponding inverse problems is accelerated stochastic proximal methods (ASPMs), with the caveat that each iteration is expensive. To overcome this issue, we propose a mini-batch quasi-Newton proximal method (BQNPM) tailored to image-reconstruction problems with total-variation regularization. It involves an efficient approach that computes a weighted proximal mapping at a cost similar to that of the proximal mapping in ASPMs. However, BQNPM requires fewer iterations than ASPMs to converge. We assess the performance of BQNPM on three-dimensional inverse-scattering problems with linear and nonlinear physical models. Our results on simulated and real data show the effectiveness and efficiency of BQNPM,

Bayesian Inversion for Nonlinear Imaging Models using Deep Generative Priors

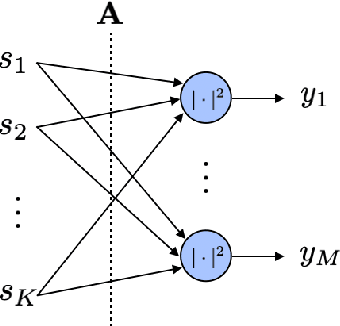
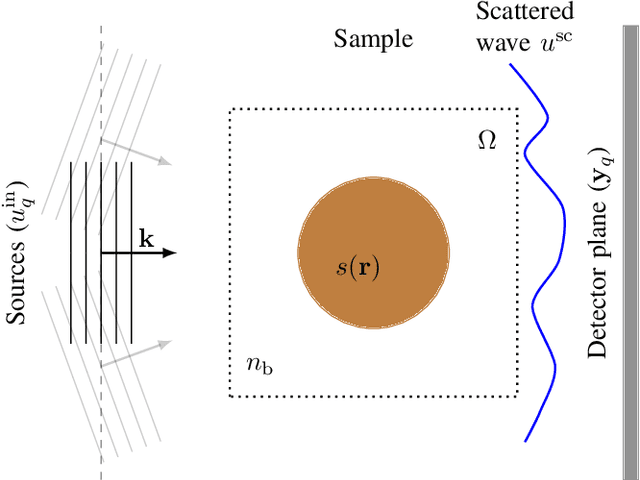
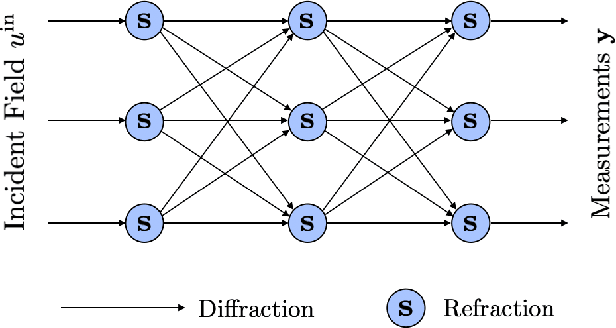
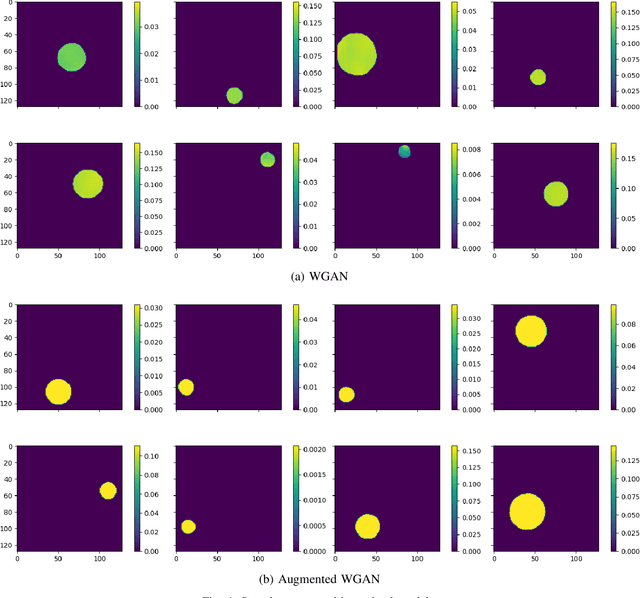
Most modern imaging systems involve a computational reconstruction pipeline to infer the image of interest from acquired measurements. The Bayesian reconstruction framework relies on the characterization of the posterior distribution, which depends on a model of the imaging system and prior knowledge on the image, for solving such inverse problems. Here, the choice of the prior distribution is critical for obtaining high-quality estimates. In this work, we use deep generative models to represent the prior distribution. We develop a posterior sampling scheme for the class of nonlinear inverse problems where the forward model has a neural-network-like structure. This class includes most existing imaging modalities. We introduce the notion of augmented generative models in order to suitably handle quantitative image recovery. We illustrate the advantages of our framework by applying it to two nonlinear imaging modalities-phase retrieval and optical diffraction tomography.

Diffraction Tomography with Helmholtz Equation: Efficient and Robust Multigrid-Based Solver

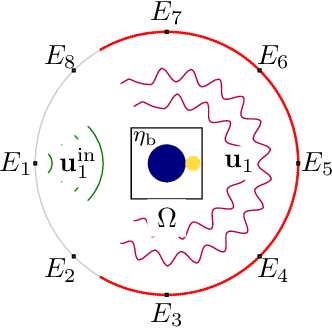
Diffraction tomography is a noninvasive technique that estimates the refractive indices of unknown objects and involves an inverse-scattering problem governed by the wave equation. Recent works have shown the benefit of nonlinear models of wave propagation that account for multiple scattering and reflections. In particular, the Lippmann-Schwinger~(LiS) model defines an inverse problem to simulate the wave propagation. Although accurate, this model is hard to solve when the samples are highly contrasted or have a large physical size. In this work, we introduce instead a Helmholtz-based nonlinear model for inverse scattering. To solve the corresponding inverse problem, we propose a robust and efficient multigrid-based solver. Moreover, we show that our method is a suitable alternative to the LiS model, especially for strongly scattering objects. Numerical experiments on simulated and real data demonstrate the effectiveness of the Helmholtz model, as well as the efficiency of the proposed multigrid method.

Optimal transport-based metric for SMLM

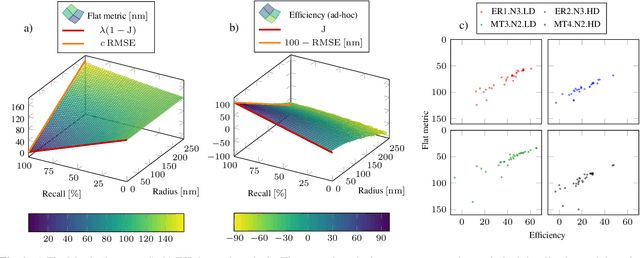
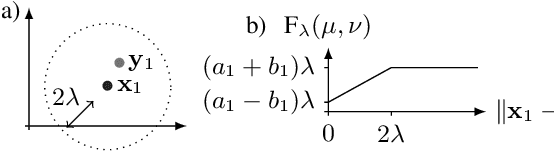
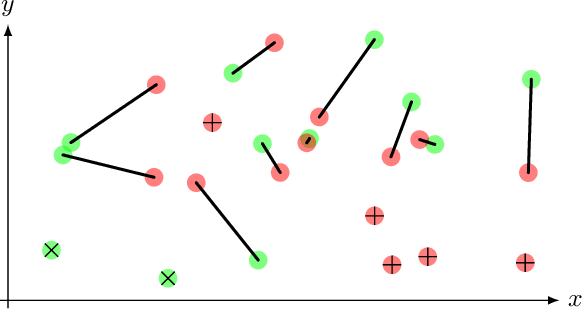
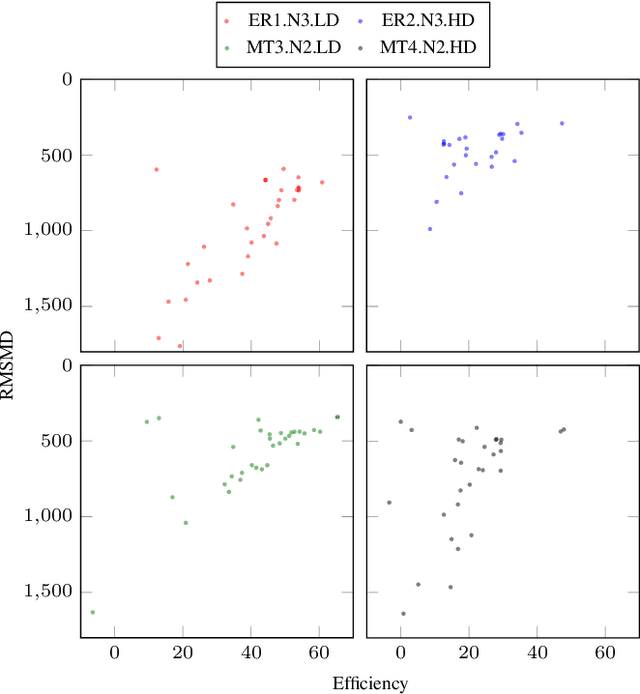
We propose the use of Flat Metric to assess the performance of reconstruction methods for single-molecule localization microscopy (SMLM)in scenarios where the ground-truth is available. Flat Metric is intimately related to the concept of optimal transport between measures of different mass, providing solid mathematical foundations for SMLM evaluation and integrating both localization and detection performance. In this paper, we introduce the foundations of Flat Metric and validate this measure by applying it to controlled synthetic examples and to data from the SMLM 2016 Challenge.

Robust Phase Unwrapping via Deep Image Prior for Quantitative Phase Imaging

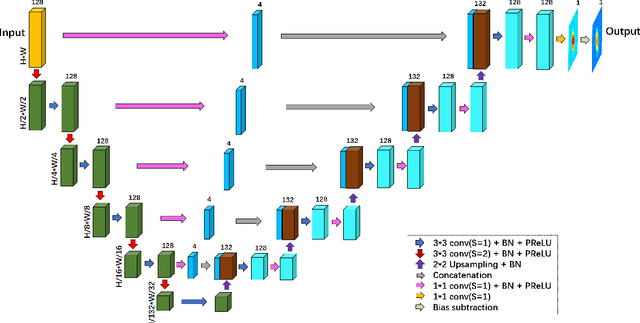
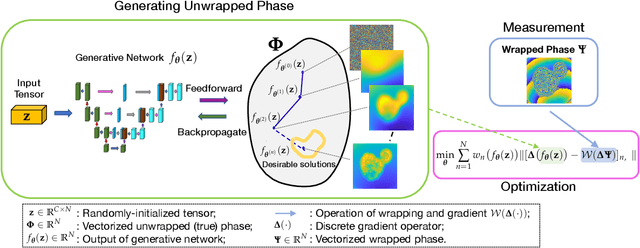
Quantitative phase imaging (QPI) is an emerging label-free technique that produces images containing morphological and dynamical information without contrast agents. Unfortunately, the phase is wrapped in most imaging system. Phase unwrapping is the computational process that recovers a more informative image. It is particularly challenging with thick and complex samples such as organoids. Recent works that rely on supervised training show that deep learning is a powerful method to unwrap the phase; however, supervised approaches require large and representative datasets which are difficult to obtain for complex biological samples. Inspired by the concept of deep image priors, we propose a deep-learning-based method that does not need any training set. Our framework relies on an untrained convolutional neural network to accurately unwrap the phase while ensuring the consistency of the measurements. We experimentally demonstrate that the proposed method faithfully recovers the phase of complex samples on both real and simulated data. Our work paves the way to reliable phase imaging of thick and complex samples with QPI.