A Mini-Batch Quasi-Newton Proximal Method for Constrained Total-Variation Nonlinear Image Reconstruction

Over the years, computational imaging with accurate nonlinear physical models has drawn considerable interest due to its ability to achieve high-quality reconstructions. However, such nonlinear models are computationally demanding. A popular choice for solving the corresponding inverse problems is accelerated stochastic proximal methods (ASPMs), with the caveat that each iteration is expensive. To overcome this issue, we propose a mini-batch quasi-Newton proximal method (BQNPM) tailored to image-reconstruction problems with total-variation regularization. It involves an efficient approach that computes a weighted proximal mapping at a cost similar to that of the proximal mapping in ASPMs. However, BQNPM requires fewer iterations than ASPMs to converge. We assess the performance of BQNPM on three-dimensional inverse-scattering problems with linear and nonlinear physical models. Our results on simulated and real data show the effectiveness and efficiency of BQNPM,

Learning Algebraic Multigrid Using Graph Neural Networks

Efficient numerical solvers for sparse linear systems are crucial in science and engineering. One of the fastest methods for solving large-scale sparse linear systems is algebraic multigrid (AMG). The main challenge in the construction of AMG algorithms is the selection of the prolongation operator -- a problem-dependent sparse matrix which governs the multiscale hierarchy of the solver and is critical to its efficiency. Over many years, numerous methods have been developed for this task, and yet there is no known single right answer except in very special cases. Here we propose a framework for learning AMG prolongation operators for linear systems with sparse symmetric positive (semi-) definite matrices. We train a single graph neural network to learn a mapping from an entire class of such matrices to prolongation operators, using an efficient unsupervised loss function. Experiments on a broad class of problems demonstrate improved convergence rates compared to classical AMG, demonstrating the potential utility of neural networks for developing sparse system solvers.

Learning to Optimize Multigrid PDE Solvers

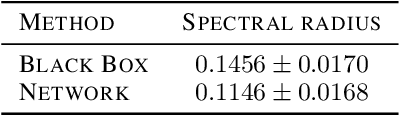
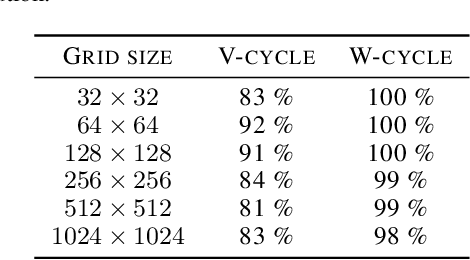
Constructing fast numerical solvers for partial differential equations (PDEs) is crucial for many scientific disciplines. A leading technique for solving large-scale PDEs is using multigrid methods. At the core of a multigrid solver is the prolongation matrix, which relates between different scales of the problem. This matrix is strongly problem-dependent, and its optimal construction is critical to the efficiency of the solver. In practice, however, devising multigrid algorithms for new problems often poses formidable challenges. In this paper we propose a framework for learning multigrid solvers. Our method learns a (single) mapping from discretized PDEs to prolongation operators for a broad class of 2D diffusion problems. We train a neural network once for the entire class of PDEs, using an efficient and unsupervised loss function. Our tests demonstrate improved convergence rates compared to the widely used Black-Box multigrid scheme, suggesting that our method successfully learned rules for constructing prolongation matrices.

A multilevel framework for sparse optimization with application to inverse covariance estimation and logistic regression

Solving l1 regularized optimization problems is common in the fields of computational biology, signal processing and machine learning. Such l1 regularization is utilized to find sparse minimizers of convex functions. A well-known example is the LASSO problem, where the l1 norm regularizes a quadratic function. A multilevel framework is presented for solving such l1 regularized sparse optimization problems efficiently. We take advantage of the expected sparseness of the solution, and create a hierarchy of problems of similar type, which is traversed in order to accelerate the optimization process. This framework is applied for solving two problems: (1) the sparse inverse covariance estimation problem, and (2) l1-regularized logistic regression. In the first problem, the inverse of an unknown covariance matrix of a multivariate normal distribution is estimated, under the assumption that it is sparse. To this end, an l1 regularized log-determinant optimization problem needs to be solved. This task is challenging especially for large-scale datasets, due to time and memory limitations. In the second problem, the l1-regularization is added to the logistic regression classification objective to reduce overfitting to the data and obtain a sparse model. Numerical experiments demonstrate the efficiency of the multilevel framework in accelerating existing iterative solvers for both of these problems.

On MMSE and MAP Denoising Under Sparse Representation Modeling Over a Unitary Dictionary

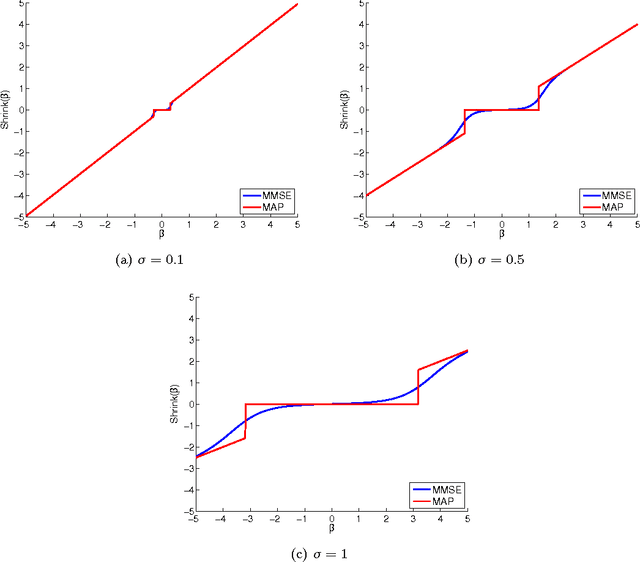
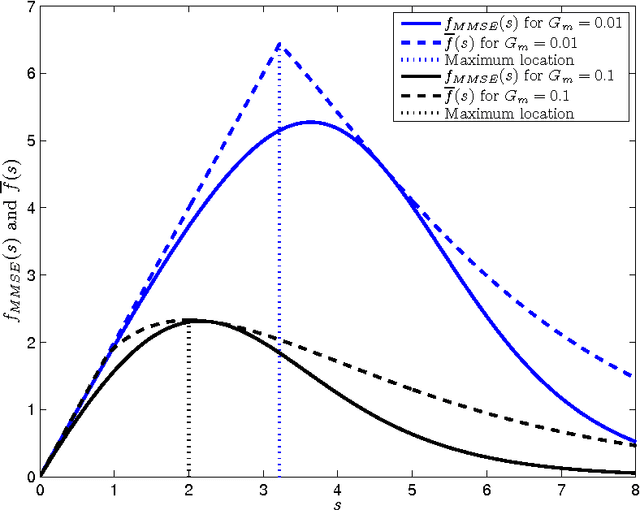
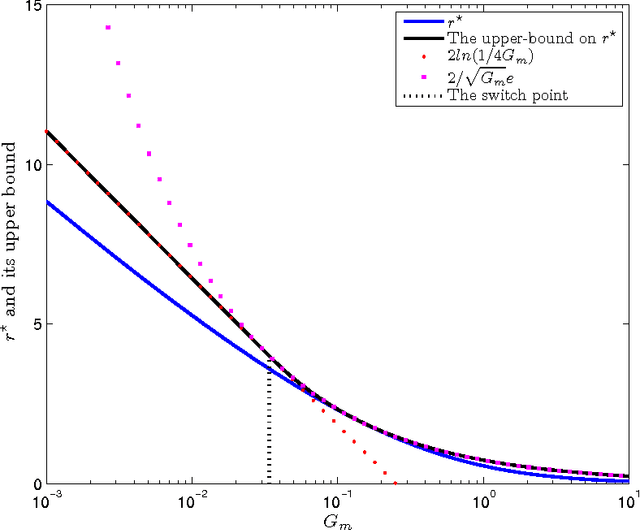
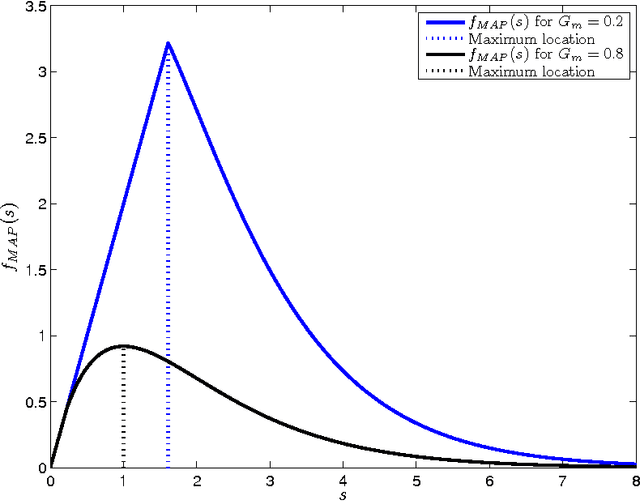
Among the many ways to model signals, a recent approach that draws considerable attention is sparse representation modeling. In this model, the signal is assumed to be generated as a random linear combination of a few atoms from a pre-specified dictionary. In this work we analyze two Bayesian denoising algorithms -- the Maximum-Aposteriori Probability (MAP) and the Minimum-Mean-Squared-Error (MMSE) estimators, under the assumption that the dictionary is unitary. It is well known that both these estimators lead to a scalar shrinkage on the transformed coefficients, albeit with a different response curve. In this work we start by deriving closed-form expressions for these shrinkage curves and then analyze their performance. Upper bounds on the MAP and the MMSE estimation errors are derived. We tie these to the error obtained by a so-called oracle estimator, where the support is given, establishing a worst-case gain-factor between the MAP/MMSE estimation errors and the oracle's performance. These denoising algorithms are demonstrated on synthetic signals and on true data (images).