Learning from Historical Activations in Graph Neural Networks

Graph Neural Networks (GNNs) have demonstrated remarkable success in various domains such as social networks, molecular chemistry, and more. A crucial component of GNNs is the pooling procedure, in which the node features calculated by the model are combined to form an informative final descriptor to be used for the downstream task. However, previous graph pooling schemes rely on the last GNN layer features as an input to the pooling or classifier layers, potentially under-utilizing important activations of previous layers produced during the forward pass of the model, which we regard as historical graph activations. This gap is particularly pronounced in cases where a node's representation can shift significantly over the course of many graph neural layers, and worsened by graph-specific challenges such as over-smoothing in deep architectures. To bridge this gap, we introduce HISTOGRAPH, a novel two-stage attention-based final aggregation layer that first applies a unified layer-wise attention over intermediate activations, followed by node-wise attention. By modeling the evolution of node representations across layers, our HISTOGRAPH leverages both the activation history of nodes and the graph structure to refine features used for final prediction. Empirical results on multiple graph classification benchmarks demonstrate that HISTOGRAPH offers strong performance that consistently improves traditional techniques, with particularly strong robustness in deep GNNs.

GradMetaNet: An Equivariant Architecture for Learning on Gradients

Gradients of neural networks encode valuable information for optimization, editing, and analysis of models. Therefore, practitioners often treat gradients as inputs to task-specific algorithms, e.g. for pruning or optimization. Recent works explore learning algorithms that operate directly on gradients but use architectures that are not specifically designed for gradient processing, limiting their applicability. In this paper, we present a principled approach for designing architectures that process gradients. Our approach is guided by three principles: (1) equivariant design that preserves neuron permutation symmetries, (2) processing sets of gradients across multiple data points to capture curvature information, and (3) efficient gradient representation through rank-1 decomposition. Based on these principles, we introduce GradMetaNet, a novel architecture for learning on gradients, constructed from simple equivariant blocks. We prove universality results for GradMetaNet, and show that previous approaches cannot approximate natural gradient-based functions that GradMetaNet can. We then demonstrate GradMetaNet's effectiveness on a diverse set of gradient-based tasks on MLPs and transformers, such as learned optimization, INR editing, and estimating loss landscape curvature.

It Takes a Graph to Know a Graph: Rewiring for Homophily with a Reference Graph

Graph Neural Networks (GNNs) excel at analyzing graph-structured data but struggle on heterophilic graphs, where connected nodes often belong to different classes. While this challenge is commonly addressed with specialized GNN architectures, graph rewiring remains an underexplored strategy in this context. We provide theoretical foundations linking edge homophily, GNN embedding smoothness, and node classification performance, motivating the need to enhance homophily. Building on this insight, we introduce a rewiring framework that increases graph homophily using a reference graph, with theoretical guarantees on the homophily of the rewired graph. To broaden applicability, we propose a label-driven diffusion approach for constructing a homophilic reference graph from node features and training labels. Through extensive simulations, we analyze how the homophily of both the original and reference graphs influences the rewired graph homophily and downstream GNN performance. We evaluate our method on 11 real-world heterophilic datasets and show that it outperforms existing rewiring techniques and specialized GNNs for heterophilic graphs, achieving improved node classification accuracy while remaining efficient and scalable to large graphs.

Efficient GNN Training Through Structure-Aware Randomized Mini-Batching

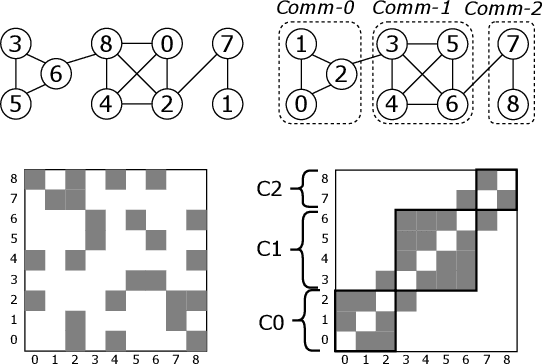
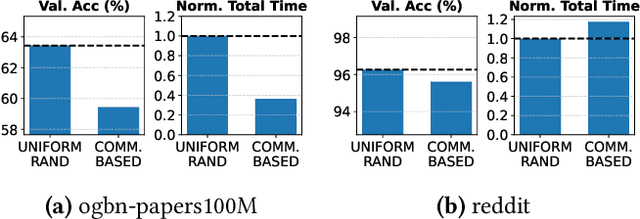
Graph Neural Networks (GNNs) enable learning on realworld graphs and mini-batch training has emerged as the de facto standard for training GNNs because it can scale to very large graphs and improve convergence. Current mini-batch construction policies largely ignore efficiency considerations of GNN training. Specifically, existing mini-batching techniques employ randomization schemes to improve accuracy and convergence. However, these randomization schemes are often agnostic to the structural properties of the graph (for eg. community structure), resulting in highly irregular memory access patterns during GNN training that make suboptimal use of on-chip GPU caches. On the other hand, while deterministic mini-batching based solely on graph structure delivers fast runtime performance, the lack of randomness compromises both the final model accuracy and training convergence speed. In this paper, we present Community-structure-aware Randomized Mini-batching (COMM-RAND), a novel methodology that bridges the gap between the above extremes. COMM-RAND allows practitioners to explore the space between pure randomness and pure graph structural awareness during mini-batch construction, leading to significantly more efficient GNN training with similar accuracy. We evaluated COMM-RAND across four popular graph learning benchmarks. COMM-RAND cuts down GNN training time by up to 2.76x (1.8x on average) while achieving an accuracy that is within 1.79% points (0.42% on average) compared to popular random mini-batching approaches.

Learning on LLM Output Signatures for gray-box LLM Behavior Analysis

Large Language Models (LLMs) have achieved widespread adoption, yet our understanding of their behavior remains limited, particularly in detecting data contamination and hallucinations. While recently proposed probing techniques provide insights through activation analysis, they require "white-box" access to model internals, often unavailable. Current "gray-box" approaches typically analyze only the probability of the actual tokens in the sequence with simple task-specific heuristics. Importantly, these methods overlook the rich information contained in the full token distribution at each processing step. To address these limitations, we propose that gray-box analysis should leverage the complete observable output of LLMs, consisting of both the previously used token probabilities as well as the complete token distribution sequences - a unified data type we term LOS (LLM Output Signature). To this end, we develop a transformer-based approach to process LOS that theoretically guarantees approximation of existing techniques while enabling more nuanced analysis. Our approach achieves superior performance on hallucination and data contamination detection in gray-box settings, significantly outperforming existing baselines. Furthermore, it demonstrates strong transfer capabilities across datasets and LLMs, suggesting that LOS captures fundamental patterns in LLM behavior. Our code is available at: https://github.com/BarSGuy/LLM-Output-Signatures-Network.

Balancing Efficiency and Expressiveness: Subgraph GNNs with Walk-Based Centrality

We propose an expressive and efficient approach that combines the strengths of two prominent extensions of Graph Neural Networks (GNNs): Subgraph GNNs and Structural Encodings (SEs). Our approach leverages walk-based centrality measures, both as a powerful form of SE and also as a subgraph selection strategy for Subgraph GNNs. By drawing a connection to perturbation analysis, we highlight the effectiveness of centrality-based sampling, and show it significantly reduces the computational burden associated with Subgraph GNNs. Further, we combine our efficient Subgraph GNN with SEs derived from the calculated centrality and demonstrate this hybrid approach, dubbed HyMN, gains in discriminative power. HyMN effectively addresses the expressiveness limitations of Message Passing Neural Networks (MPNNs) while mitigating the computational costs of Subgraph GNNs. Through a series of experiments on synthetic and real-world tasks, we show it outperforms other subgraph sampling approaches while being competitive with full-bag Subgraph GNNs and other state-of-the-art approaches with a notably reduced runtime.

Towards Foundation Models on Graphs: An Analysis on Cross-Dataset Transfer of Pretrained GNNs

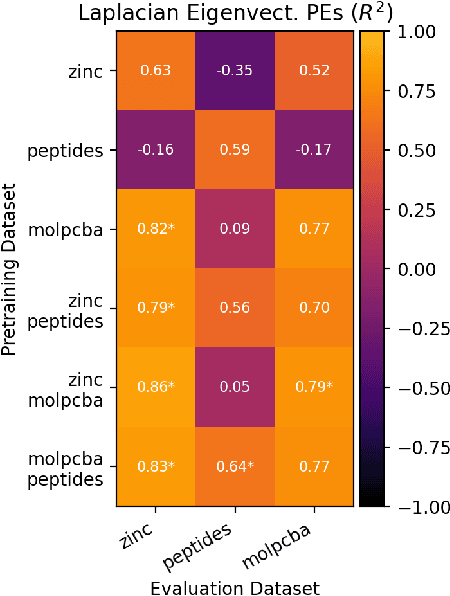
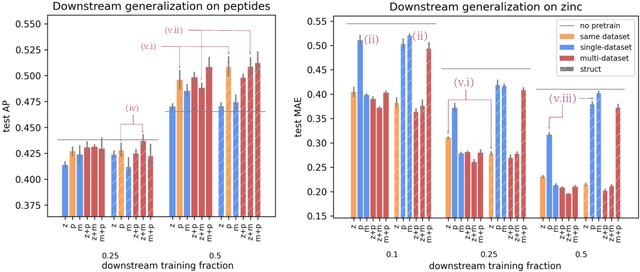
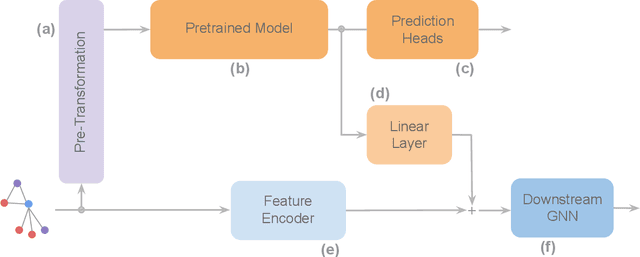
To develop a preliminary understanding towards Graph Foundation Models, we study the extent to which pretrained Graph Neural Networks can be applied across datasets, an effort requiring to be agnostic to dataset-specific features and their encodings. We build upon a purely structural pretraining approach and propose an extension to capture feature information while still being feature-agnostic. We evaluate pretrained models on downstream tasks for varying amounts of training samples and choices of pretraining datasets. Our preliminary results indicate that embeddings from pretrained models improve generalization only with enough downstream data points and in a degree which depends on the quantity and properties of pretraining data. Feature information can lead to improvements, but currently requires some similarities between pretraining and downstream feature spaces.

On the Reconstruction of Training Data from Group Invariant Networks

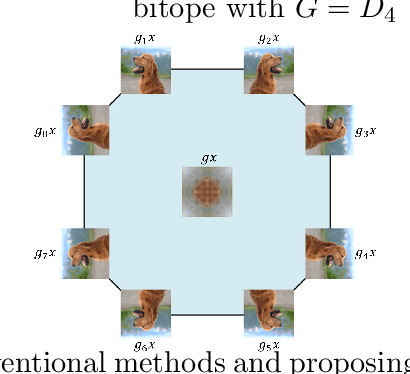
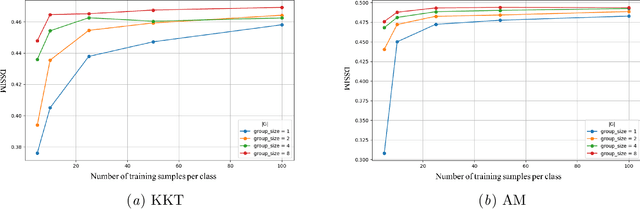
Reconstructing training data from trained neural networks is an active area of research with significant implications for privacy and explainability. Recent advances have demonstrated the feasibility of this process for several data types. However, reconstructing data from group-invariant neural networks poses distinct challenges that remain largely unexplored. This paper addresses this gap by first formulating the problem and discussing some of its basic properties. We then provide an experimental evaluation demonstrating that conventional reconstruction techniques are inadequate in this scenario. Specifically, we observe that the resulting data reconstructions gravitate toward symmetric inputs on which the group acts trivially, leading to poor-quality results. Finally, we propose two novel methods aiming to improve reconstruction in this setup and present promising preliminary experimental results. Our work sheds light on the complexities of reconstructing data from group invariant neural networks and offers potential avenues for future research in this domain.

Learning on LoRAs: GL-Equivariant Processing of Low-Rank Weight Spaces for Large Finetuned Models

Low-rank adaptations (LoRAs) have revolutionized the finetuning of large foundation models, enabling efficient adaptation even with limited computational resources. The resulting proliferation of LoRAs presents exciting opportunities for applying machine learning techniques that take these low-rank weights themselves as inputs. In this paper, we investigate the potential of Learning on LoRAs (LoL), a paradigm where LoRA weights serve as input to machine learning models. For instance, an LoL model that takes in LoRA weights as inputs could predict the performance of the finetuned model on downstream tasks, detect potentially harmful finetunes, or even generate novel model edits without traditional training methods. We first identify the inherent parameter symmetries of low rank decompositions of weights, which differ significantly from the parameter symmetries of standard neural networks. To efficiently process LoRA weights, we develop several symmetry-aware invariant or equivariant LoL models, using tools such as canonicalization, invariant featurization, and equivariant layers. We finetune thousands of text-to-image diffusion models and language models to collect datasets of LoRAs. In numerical experiments on these datasets, we show that our LoL architectures are capable of processing low rank weight decompositions to predict CLIP score, finetuning data attributes, finetuning data membership, and accuracy on downstream tasks.

Foldable SuperNets: Scalable Merging of Transformers with Different Initializations and Tasks

Many recent methods aim to merge neural networks (NNs) with identical architectures trained on different tasks to obtain a single multi-task model. Most existing works tackle the simpler setup of merging NNs initialized from a common pre-trained network, where simple heuristics like weight averaging work well. This work targets a more challenging goal: merging large transformers trained on different tasks from distinct initializations. First, we demonstrate that traditional merging methods fail catastrophically in this setup. To overcome this challenge, we propose Foldable SuperNet Merge (FS-Merge), a method that optimizes a SuperNet to fuse the original models using a feature reconstruction loss. FS-Merge is simple, data-efficient, and capable of merging models of varying widths. We test FS-Merge against existing methods, including knowledge distillation, on MLPs and transformers across various settings, sizes, tasks, and modalities. FS-Merge consistently outperforms them, achieving SOTA results, particularly in limited data scenarios.