Learning on LoRAs: GL-Equivariant Processing of Low-Rank Weight Spaces for Large Finetuned Models

Low-rank adaptations (LoRAs) have revolutionized the finetuning of large foundation models, enabling efficient adaptation even with limited computational resources. The resulting proliferation of LoRAs presents exciting opportunities for applying machine learning techniques that take these low-rank weights themselves as inputs. In this paper, we investigate the potential of Learning on LoRAs (LoL), a paradigm where LoRA weights serve as input to machine learning models. For instance, an LoL model that takes in LoRA weights as inputs could predict the performance of the finetuned model on downstream tasks, detect potentially harmful finetunes, or even generate novel model edits without traditional training methods. We first identify the inherent parameter symmetries of low rank decompositions of weights, which differ significantly from the parameter symmetries of standard neural networks. To efficiently process LoRA weights, we develop several symmetry-aware invariant or equivariant LoL models, using tools such as canonicalization, invariant featurization, and equivariant layers. We finetune thousands of text-to-image diffusion models and language models to collect datasets of LoRAs. In numerical experiments on these datasets, we show that our LoL architectures are capable of processing low rank weight decompositions to predict CLIP score, finetuning data attributes, finetuning data membership, and accuracy on downstream tasks.

Topological Blind Spots: Understanding and Extending Topological Deep Learning Through the Lens of Expressivity

Topological deep learning (TDL) facilitates learning from data represented by topological structures. The primary model utilized in this setting is higher-order message-passing (HOMP), which extends traditional graph message-passing neural networks (MPNN) to diverse topological domains. Given the significant expressivity limitations of MPNNs, our paper aims to explore both the strengths and weaknesses of HOMP's expressive power and subsequently design novel architectures to address these limitations. We approach this from several perspectives: First, we demonstrate HOMP's inability to distinguish between topological objects based on fundamental topological and metric properties such as diameter, orientability, planarity, and homology. Second, we show HOMP's limitations in fully leveraging the topological structure of objects constructed using common lifting and pooling operators on graphs. Finally, we compare HOMP's expressive power to hypergraph networks, which are the most extensively studied TDL methods. We then develop two new classes of TDL models: multi-cellular networks (MCN) and scalable multi-cellular networks (SMCN). These models draw inspiration from expressive graph architectures. While MCN can reach full expressivity but is highly unscalable, SMCN offers a more scalable alternative that still mitigates many of HOMP's expressivity limitations. Finally, we construct a synthetic dataset, where TDL models are tasked with separating pairs of topological objects based on basic topological properties. We demonstrate that while HOMP is unable to distinguish between any of the pairs in the dataset, SMCN successfully distinguishes all pairs, empirically validating our theoretical findings. Our work opens a new design space and new opportunities for TDL, paving the way for more expressive and versatile models.

Variational Inference Failures Under Model Symmetries: Permutation Invariant Posteriors for Bayesian Neural Networks

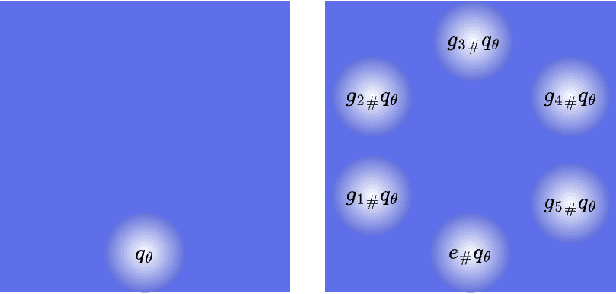
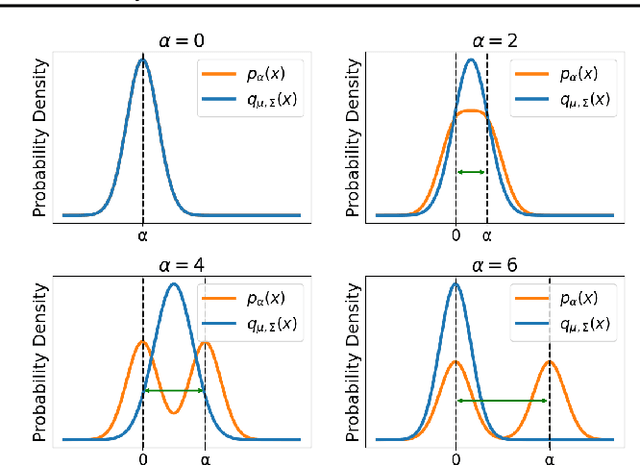
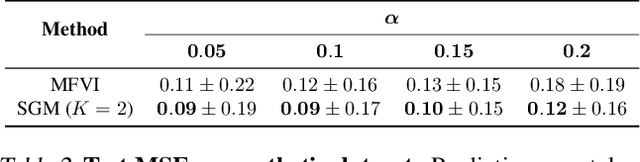
Weight space symmetries in neural network architectures, such as permutation symmetries in MLPs, give rise to Bayesian neural network (BNN) posteriors with many equivalent modes. This multimodality poses a challenge for variational inference (VI) techniques, which typically rely on approximating the posterior with a unimodal distribution. In this work, we investigate the impact of weight space permutation symmetries on VI. We demonstrate, both theoretically and empirically, that these symmetries lead to biases in the approximate posterior, which degrade predictive performance and posterior fit if not explicitly accounted for. To mitigate this behavior, we leverage the symmetric structure of the posterior and devise a symmetrization mechanism for constructing permutation invariant variational posteriors. We show that the symmetrized distribution has a strictly better fit to the true posterior, and that it can be trained using the original ELBO objective with a modified KL regularization term. We demonstrate experimentally that our approach mitigates the aforementioned biases and results in improved predictions and a higher ELBO.