Variational Inference Failures Under Model Symmetries: Permutation Invariant Posteriors for Bayesian Neural Networks
Paper and Code
Aug 10, 2024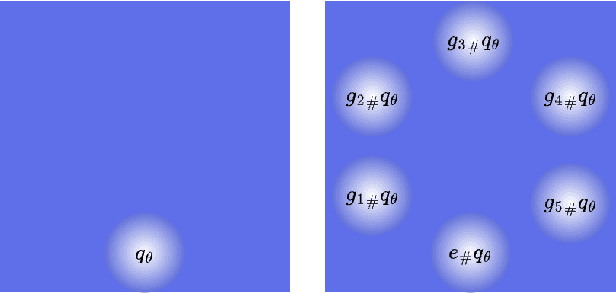

Weight space symmetries in neural network architectures, such as permutation symmetries in MLPs, give rise to Bayesian neural network (BNN) posteriors with many equivalent modes. This multimodality poses a challenge for variational inference (VI) techniques, which typically rely on approximating the posterior with a unimodal distribution. In this work, we investigate the impact of weight space permutation symmetries on VI. We demonstrate, both theoretically and empirically, that these symmetries lead to biases in the approximate posterior, which degrade predictive performance and posterior fit if not explicitly accounted for. To mitigate this behavior, we leverage the symmetric structure of the posterior and devise a symmetrization mechanism for constructing permutation invariant variational posteriors. We show that the symmetrized distribution has a strictly better fit to the true posterior, and that it can be trained using the original ELBO objective with a modified KL regularization term. We demonstrate experimentally that our approach mitigates the aforementioned biases and results in improved predictions and a higher ELBO.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge