PSyDUCK: Training-Free Steganography for Latent Diffusion

Recent advances in AI-generated steganography highlight its potential for safeguarding the privacy of vulnerable democratic actors, including aid workers, journalists, and whistleblowers operating in oppressive regimes. In this work, we address current limitations and establish the foundations for large-throughput generative steganography. We introduce a novel approach that enables secure and efficient steganography within latent diffusion models. We show empirically that our methods perform well across a variety of open-source latent diffusion models, particularly in generative image and video tasks.

Rethinking Aleatoric and Epistemic Uncertainty

The ideas of aleatoric and epistemic uncertainty are widely used to reason about the probabilistic predictions of machine-learning models. We identify incoherence in existing discussions of these ideas and suggest this stems from the aleatoric-epistemic view being insufficiently expressive to capture all of the distinct quantities that researchers are interested in. To explain and address this we derive a simple delineation of different model-based uncertainties and the data-generating processes associated with training and evaluation. Using this in place of the aleatoric-epistemic view could produce clearer discourse as the field moves forward.

A Meta-Learning Approach to Bayesian Causal Discovery

Discovering a unique causal structure is difficult due to both inherent identifiability issues, and the consequences of finite data. As such, uncertainty over causal structures, such as those obtained from a Bayesian posterior, are often necessary for downstream tasks. Finding an accurate approximation to this posterior is challenging, due to the large number of possible causal graphs, as well as the difficulty in the subproblem of finding posteriors over the functional relationships of the causal edges. Recent works have used meta-learning to view the problem of estimating the maximum a-posteriori causal graph as supervised learning. Yet, these methods are limited when estimating the full posterior as they fail to encode key properties of the posterior, such as correlation between edges and permutation equivariance with respect to nodes. Further, these methods also cannot reliably sample from the posterior over causal structures. To address these limitations, we propose a Bayesian meta learning model that allows for sampling causal structures from the posterior and encodes these key properties. We compare our meta-Bayesian causal discovery against existing Bayesian causal discovery methods, demonstrating the advantages of directly learning a posterior over causal structure.

Continuous Bayesian Model Selection for Multivariate Causal Discovery

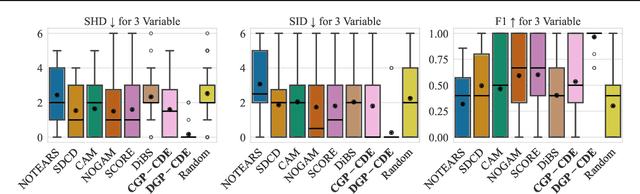
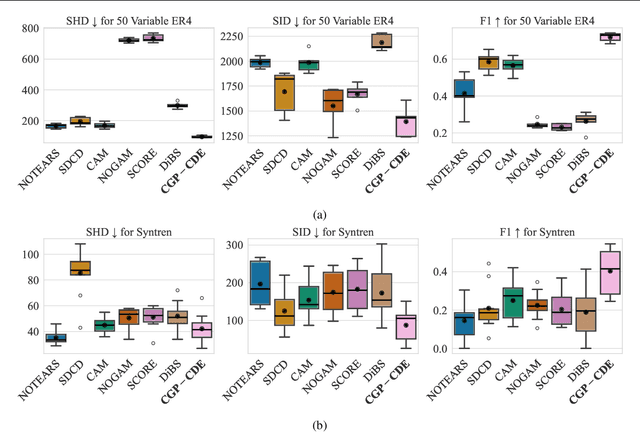
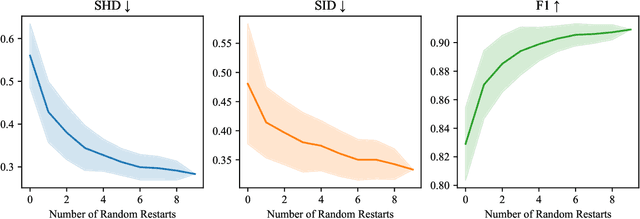
Current causal discovery approaches require restrictive model assumptions or assume access to interventional data to ensure structure identifiability. These assumptions often do not hold in real-world applications leading to a loss of guarantees and poor accuracy in practice. Recent work has shown that, in the bivariate case, Bayesian model selection can greatly improve accuracy by exchanging restrictive modelling for more flexible assumptions, at the cost of a small probability of error. We extend the Bayesian model selection approach to the important multivariate setting by making the large discrete selection problem scalable through a continuous relaxation. We demonstrate how for our choice of Bayesian non-parametric model, the Causal Gaussian Process Conditional Density Estimator (CGP-CDE), an adjacency matrix can be constructed from the model hyperparameters. This adjacency matrix is then optimised using the marginal likelihood and an acyclicity regulariser, outputting the maximum a posteriori causal graph. We demonstrate the competitiveness of our approach on both synthetic and real-world datasets, showing it is possible to perform multivariate causal discovery without infeasible assumptions using Bayesian model selection.

Noether's razor: Learning Conserved Quantities

Symmetries have proven useful in machine learning models, improving generalisation and overall performance. At the same time, recent advancements in learning dynamical systems rely on modelling the underlying Hamiltonian to guarantee the conservation of energy. These approaches can be connected via a seminal result in mathematical physics: Noether's theorem, which states that symmetries in a dynamical system correspond to conserved quantities. This work uses Noether's theorem to parameterise symmetries as learnable conserved quantities. We then allow conserved quantities and associated symmetries to be learned directly from train data through approximate Bayesian model selection, jointly with the regular training procedure. As training objective, we derive a variational lower bound to the marginal likelihood. The objective automatically embodies an Occam's Razor effect that avoids collapse of conservation laws to the trivial constant, without the need to manually add and tune additional regularisers. We demonstrate a proof-of-principle on $n$-harmonic oscillators and $n$-body systems. We find that our method correctly identifies the correct conserved quantities and U($n$) and SE($n$) symmetry groups, improving overall performance and predictive accuracy on test data.

"How Big is Big Enough?" Adjusting Model Size in Continual Gaussian Processes

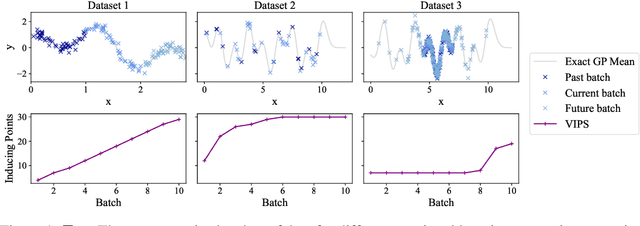
For many machine learning methods, creating a model requires setting a parameter that controls the model's capacity before training, e.g.~number of neurons in DNNs, or inducing points in GPs. Increasing capacity improves performance until all the information from the dataset is captured. After this point, computational cost keeps increasing, without improved performance. This leads to the question ``How big is big enough?'' We investigate this problem for Gaussian processes (single-layer neural networks) in continual learning. Here, data becomes available incrementally, and the final dataset size will therefore not be known before training, preventing the use of heuristics for setting the model size. We provide a method that automatically adjusts this, while maintaining near-optimal performance, and show that a single hyperparameter setting for our method performs well across datasets with a wide range of properties.

Variational Inference Failures Under Model Symmetries: Permutation Invariant Posteriors for Bayesian Neural Networks

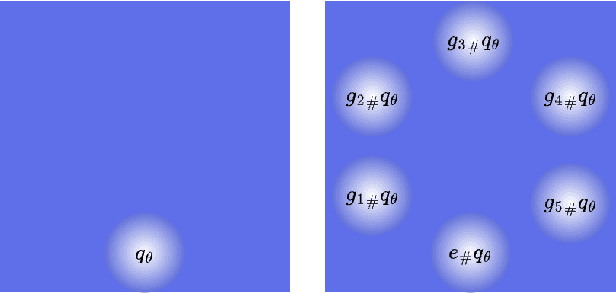
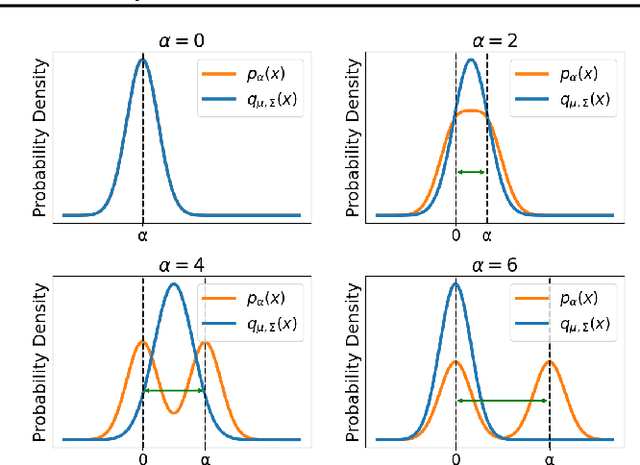
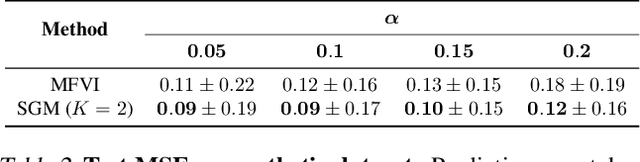
Weight space symmetries in neural network architectures, such as permutation symmetries in MLPs, give rise to Bayesian neural network (BNN) posteriors with many equivalent modes. This multimodality poses a challenge for variational inference (VI) techniques, which typically rely on approximating the posterior with a unimodal distribution. In this work, we investigate the impact of weight space permutation symmetries on VI. We demonstrate, both theoretically and empirically, that these symmetries lead to biases in the approximate posterior, which degrade predictive performance and posterior fit if not explicitly accounted for. To mitigate this behavior, we leverage the symmetric structure of the posterior and devise a symmetrization mechanism for constructing permutation invariant variational posteriors. We show that the symmetrized distribution has a strictly better fit to the true posterior, and that it can be trained using the original ELBO objective with a modified KL regularization term. We demonstrate experimentally that our approach mitigates the aforementioned biases and results in improved predictions and a higher ELBO.

System-Aware Neural ODE Processes for Few-Shot Bayesian Optimization

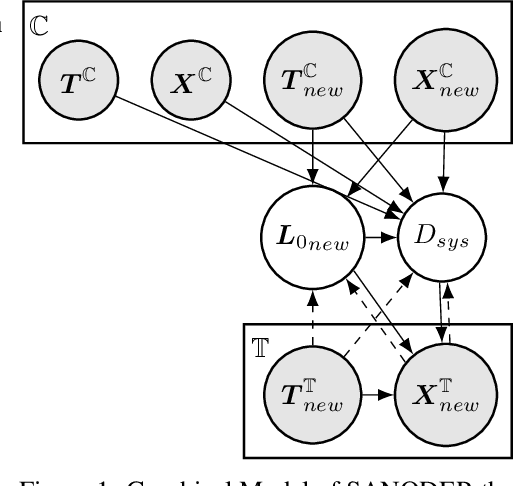
We consider the problem of optimizing initial conditions and timing in dynamical systems governed by unknown ordinary differential equations (ODEs), where evaluating different initial conditions is costly and there are constraints on observation times. To identify the optimal conditions within several trials, we introduce a few-shot Bayesian Optimization (BO) framework based on the system's prior information. At the core of our approach is the System-Aware Neural ODE Processes (SANODEP), an extension of Neural ODE Processes (NODEP) designed to meta-learn ODE systems from multiple trajectories using a novel context embedding block. Additionally, we propose a multi-scenario loss function specifically for optimization purposes. Our two-stage BO framework effectively incorporates search space constraints, enabling efficient optimization of both initial conditions and observation timings. We conduct extensive experiments showcasing SANODEP's potential for few-shot BO. We also explore SANODEP's adaptability to varying levels of prior information, highlighting the trade-off between prior flexibility and model fitting accuracy.

Transfer Learning Bayesian Optimization to Design Competitor DNA Molecules for Use in Diagnostic Assays

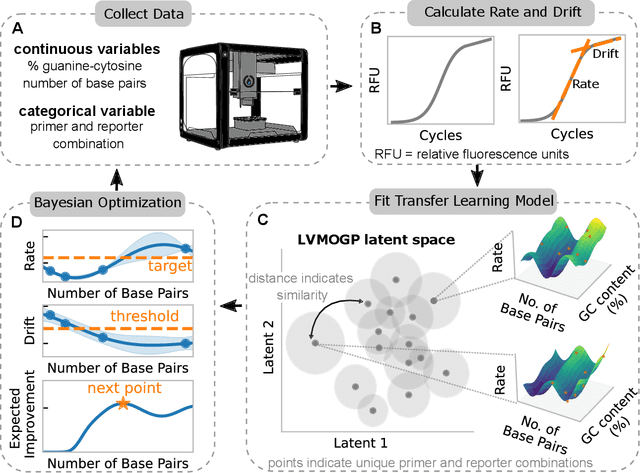
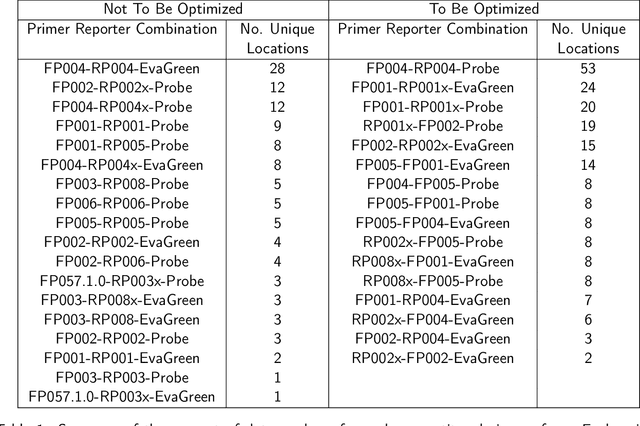
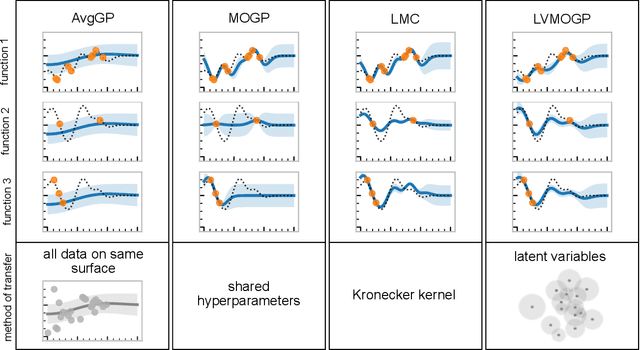
With the rise in engineered biomolecular devices, there is an increased need for tailor-made biological sequences. Often, many similar biological sequences need to be made for a specific application meaning numerous, sometimes prohibitively expensive, lab experiments are necessary for their optimization. This paper presents a transfer learning design of experiments workflow to make this development feasible. By combining a transfer learning surrogate model with Bayesian optimization, we show how the total number of experiments can be reduced by sharing information between optimization tasks. We demonstrate the reduction in the number of experiments using data from the development of DNA competitors for use in an amplification-based diagnostic assay. We use cross-validation to compare the predictive accuracy of different transfer learning models, and then compare the performance of the models for both single objective and penalized optimization tasks.

Recommendations for Baselines and Benchmarking Approximate Gaussian Processes

Gaussian processes (GPs) are a mature and widely-used component of the ML toolbox. One of their desirable qualities is automatic hyperparameter selection, which allows for training without user intervention. However, in many realistic settings, approximations are typically needed, which typically do require tuning. We argue that this requirement for tuning complicates evaluation, which has led to a lack of a clear recommendations on which method should be used in which situation. To address this, we make recommendations for comparing GP approximations based on a specification of what a user should expect from a method. In addition, we develop a training procedure for the variational method of Titsias [2009] that leaves no choices to the user, and show that this is a strong baseline that meets our specification. We conclude that benchmarking according to our suggestions gives a clearer view of the current state of the field, and uncovers problems that are still open that future papers should address.