System-Aware Neural ODE Processes for Few-Shot Bayesian Optimization

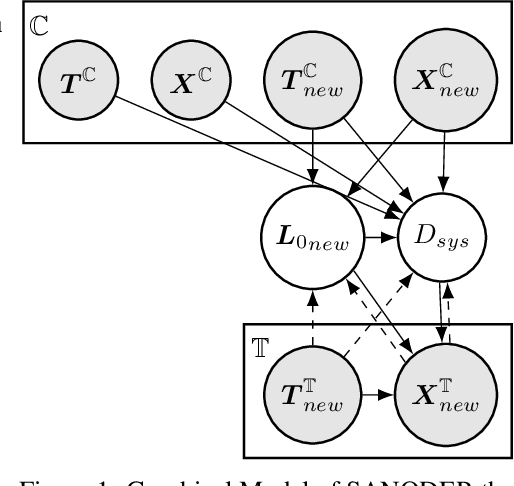
We consider the problem of optimizing initial conditions and timing in dynamical systems governed by unknown ordinary differential equations (ODEs), where evaluating different initial conditions is costly and there are constraints on observation times. To identify the optimal conditions within several trials, we introduce a few-shot Bayesian Optimization (BO) framework based on the system's prior information. At the core of our approach is the System-Aware Neural ODE Processes (SANODEP), an extension of Neural ODE Processes (NODEP) designed to meta-learn ODE systems from multiple trajectories using a novel context embedding block. Additionally, we propose a multi-scenario loss function specifically for optimization purposes. Our two-stage BO framework effectively incorporates search space constraints, enabling efficient optimization of both initial conditions and observation timings. We conduct extensive experiments showcasing SANODEP's potential for few-shot BO. We also explore SANODEP's adaptability to varying levels of prior information, highlighting the trade-off between prior flexibility and model fitting accuracy.

Transition Constrained Bayesian Optimization via Markov Decision Processes

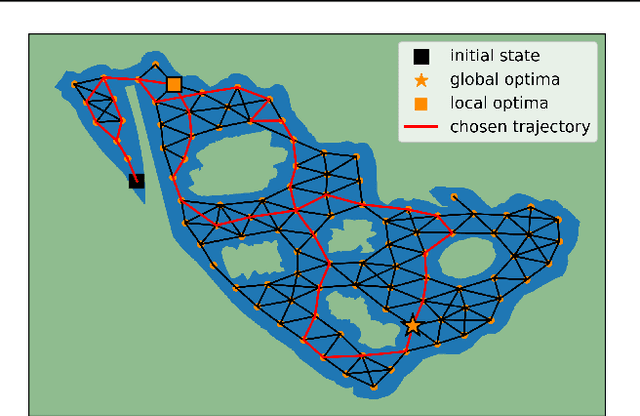
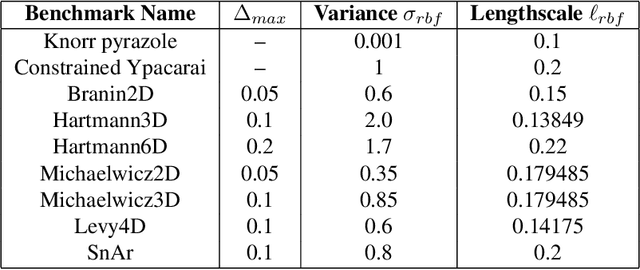
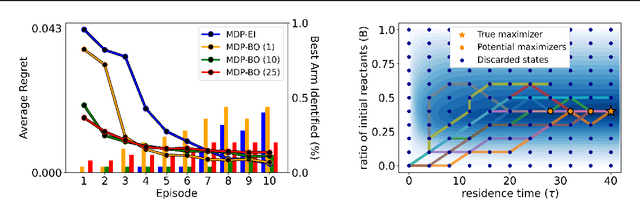
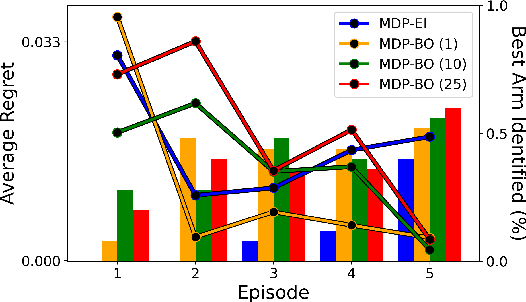
Bayesian optimization is a methodology to optimize black-box functions. Traditionally, it focuses on the setting where you can arbitrarily query the search space. However, many real-life problems do not offer this flexibility; in particular, the search space of the next query may depend on previous ones. Example challenges arise in the physical sciences in the form of local movement constraints, required monotonicity in certain variables, and transitions influencing the accuracy of measurements. Altogether, such transition constraints necessitate a form of planning. This work extends Bayesian optimization via the framework of Markov Decision Processes, iteratively solving a tractable linearization of our objective using reinforcement learning to obtain a policy that plans ahead over long horizons. The resulting policy is potentially history-dependent and non-Markovian. We showcase applications in chemical reactor optimization, informative path planning, machine calibration, and other synthetic examples.

Practical Path-based Bayesian Optimization

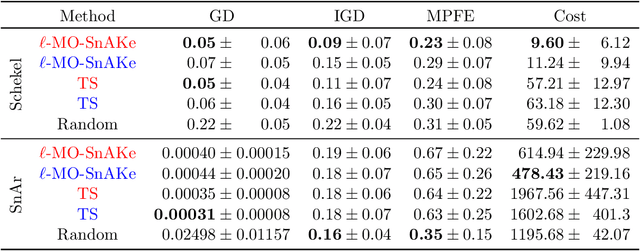
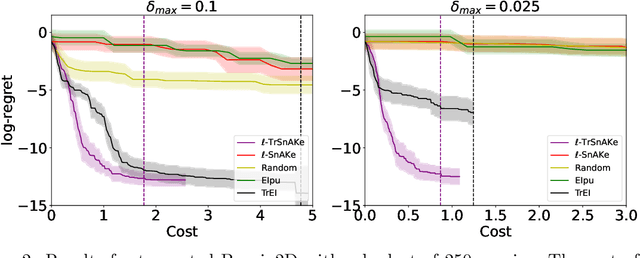
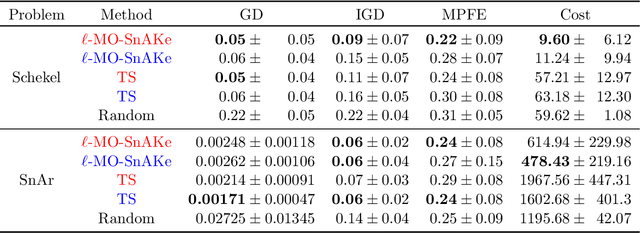
There has been a surge in interest in data-driven experimental design with applications to chemical engineering and drug manufacturing. Bayesian optimization (BO) has proven to be adaptable to such cases, since we can model the reactions of interest as expensive black-box functions. Sometimes, the cost of this black-box functions can be separated into two parts: (a) the cost of the experiment itself, and (b) the cost of changing the input parameters. In this short paper, we extend the SnAKe algorithm to deal with both types of costs simultaneously. We further propose extensions to the case of a maximum allowable input change, as well as to the multi-objective setting.

Combining Multi-Fidelity Modelling and Asynchronous Batch Bayesian Optimization

Bayesian Optimization is a useful tool for experiment design. Unfortunately, the classical, sequential setting of Bayesian Optimization does not translate well into laboratory experiments, for instance battery design, where measurements may come from different sources and their evaluations may require significant waiting times. Multi-fidelity Bayesian Optimization addresses the setting with measurements from different sources. Asynchronous batch Bayesian Optimization provides a framework to select new experiments before the results of the prior experiments are revealed. This paper proposes an algorithm combining multi-fidelity and asynchronous batch methods. We empirically study the algorithm behavior, and show it can outperform single-fidelity batch methods and multi-fidelity sequential methods. As an application, we consider designing electrode materials for optimal performance in pouch cells using experiments with coin cells to approximate battery performance.

SnAKe: Bayesian Optimization with Pathwise Exploration

Bayesian Optimization is a very effective tool for optimizing expensive black-box functions. Inspired by applications developing and characterizing reaction chemistry using droplet microfluidic reactors, we consider a novel setting where the expense of evaluating the function can increase significantly when making large input changes between iterations. We further assume we are working asynchronously, meaning we have to decide on new queries before we finish evaluating previous experiments. This paper investigates the problem and introduces 'Sequential Bayesian Optimization via Adaptive Connecting Samples' (SnAKe), which provides a solution by considering future queries and preemptively building optimization paths that minimize input costs. We investigate some convergence properties and empirically show that the algorithm is able to achieve regret similar to classical Bayesian Optimization algorithms in both the synchronous and asynchronous settings, while reducing the input costs significantly.