What Does It Mean to Be a Transformer? Insights from a Theoretical Hessian Analysis

The Transformer architecture has inarguably revolutionized deep learning, overtaking classical architectures like multi-layer perceptrons (MLPs) and convolutional neural networks (CNNs). At its core, the attention block differs in form and functionality from most other architectural components in deep learning -- to the extent that Transformers are often accompanied by adaptive optimizers, layer normalization, learning rate warmup, and more, in comparison to MLPs/CNNs. The root causes behind these outward manifestations, and the precise mechanisms that govern them, remain poorly understood. In this work, we bridge this gap by providing a fundamental understanding of what distinguishes the Transformer from the other architectures -- grounded in a theoretical comparison of the (loss) Hessian. Concretely, for a single self-attention layer, (a) we first entirely derive the Transformer's Hessian and express it in matrix derivatives; (b) we then characterize it in terms of data, weight, and attention moment dependencies; and (c) while doing so further highlight the important structural differences to the Hessian of classical networks. Our results suggest that various common architectural and optimization choices in Transformers can be traced back to their highly non-linear dependencies on the data and weight matrices, which vary heterogeneously across parameters. Ultimately, our findings provide a deeper understanding of the Transformer's unique optimization landscape and the challenges it poses.

Standardizing Structural Causal Models

Synthetic datasets generated by structural causal models (SCMs) are commonly used for benchmarking causal structure learning algorithms. However, the variances and pairwise correlations in SCM data tend to increase along the causal ordering. Several popular algorithms exploit these artifacts, possibly leading to conclusions that do not generalize to real-world settings. Existing metrics like $\operatorname{Var}$-sortability and $\operatorname{R^2}$-sortability quantify these patterns, but they do not provide tools to remedy them. To address this, we propose internally-standardized structural causal models (iSCMs), a modification of SCMs that introduces a standardization operation at each variable during the generative process. By construction, iSCMs are not $\operatorname{Var}$-sortable, and as we show experimentally, not $\operatorname{R^2}$-sortable either for commonly-used graph families. Moreover, contrary to the post-hoc standardization of data generated by standard SCMs, we prove that linear iSCMs are less identifiable from prior knowledge on the weights and do not collapse to deterministic relationships in large systems, which may make iSCMs a useful model in causal inference beyond the benchmarking problem studied here.

Transition Constrained Bayesian Optimization via Markov Decision Processes

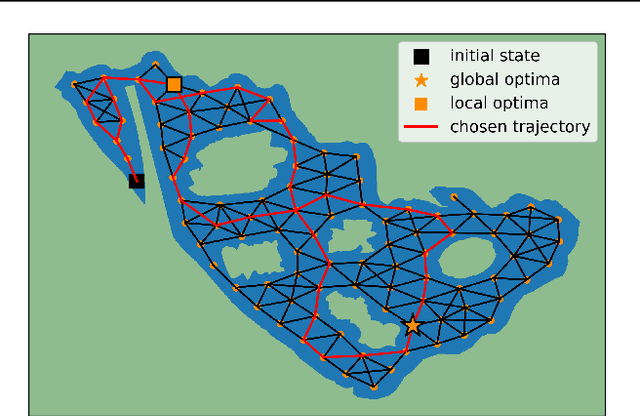
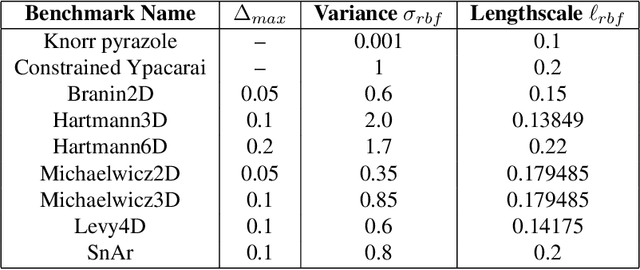
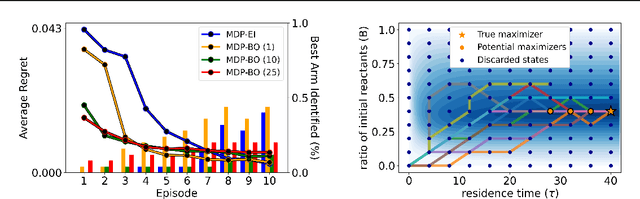
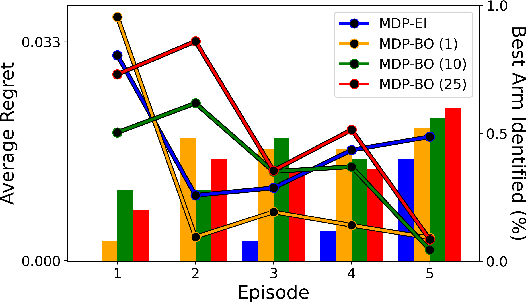
Bayesian optimization is a methodology to optimize black-box functions. Traditionally, it focuses on the setting where you can arbitrarily query the search space. However, many real-life problems do not offer this flexibility; in particular, the search space of the next query may depend on previous ones. Example challenges arise in the physical sciences in the form of local movement constraints, required monotonicity in certain variables, and transitions influencing the accuracy of measurements. Altogether, such transition constraints necessitate a form of planning. This work extends Bayesian optimization via the framework of Markov Decision Processes, iteratively solving a tractable linearization of our objective using reinforcement learning to obtain a policy that plans ahead over long horizons. The resulting policy is potentially history-dependent and non-Markovian. We showcase applications in chemical reactor optimization, informative path planning, machine calibration, and other synthetic examples.

Estimating value at risk: LSTM vs. GARCH

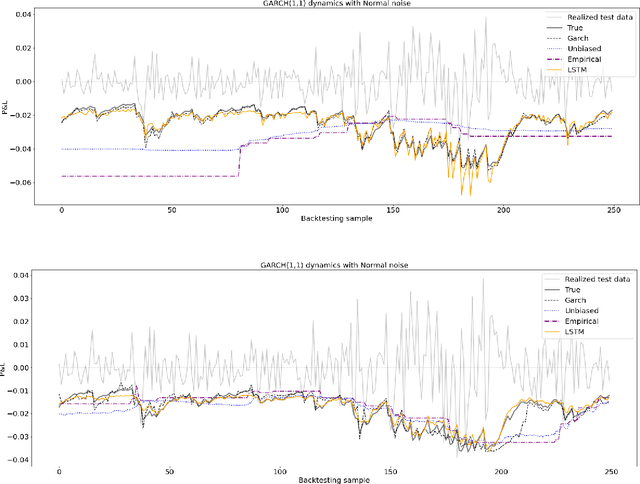
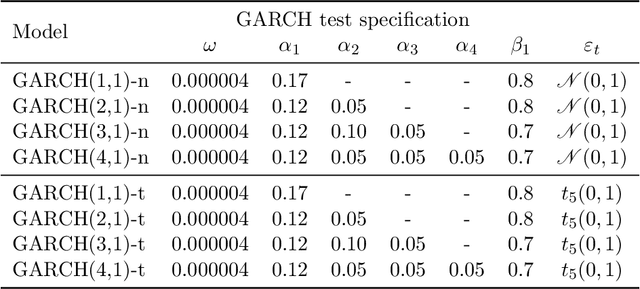
Estimating value-at-risk on time series data with possibly heteroscedastic dynamics is a highly challenging task. Typically, we face a small data problem in combination with a high degree of non-linearity, causing difficulties for both classical and machine-learning estimation algorithms. In this paper, we propose a novel value-at-risk estimator using a long short-term memory (LSTM) neural network and compare its performance to benchmark GARCH estimators. Our results indicate that even for a relatively short time series, the LSTM could be used to refine or monitor risk estimation processes and correctly identify the underlying risk dynamics in a non-parametric fashion. We evaluate the estimator on both simulated and market data with a focus on heteroscedasticity, finding that LSTM exhibits a similar performance to GARCH estimators on simulated data, whereas on real market data it is more sensitive towards increasing or decreasing volatility and outperforms all existing estimators of value-at-risk in terms of exception rate and mean quantile score.