Standardizing Structural Causal Models

Synthetic datasets generated by structural causal models (SCMs) are commonly used for benchmarking causal structure learning algorithms. However, the variances and pairwise correlations in SCM data tend to increase along the causal ordering. Several popular algorithms exploit these artifacts, possibly leading to conclusions that do not generalize to real-world settings. Existing metrics like $\operatorname{Var}$-sortability and $\operatorname{R^2}$-sortability quantify these patterns, but they do not provide tools to remedy them. To address this, we propose internally-standardized structural causal models (iSCMs), a modification of SCMs that introduces a standardization operation at each variable during the generative process. By construction, iSCMs are not $\operatorname{Var}$-sortable, and as we show experimentally, not $\operatorname{R^2}$-sortable either for commonly-used graph families. Moreover, contrary to the post-hoc standardization of data generated by standard SCMs, we prove that linear iSCMs are less identifiable from prior knowledge on the weights and do not collapse to deterministic relationships in large systems, which may make iSCMs a useful model in causal inference beyond the benchmarking problem studied here.

Model-based Causal Bayesian Optimization

In Causal Bayesian Optimization (CBO), an agent intervenes on an unknown structural causal model to maximize a downstream reward variable. In this paper, we consider the generalization where other agents or external events also intervene on the system, which is key for enabling adaptiveness to non-stationarities such as weather changes, market forces, or adversaries. We formalize this generalization of CBO as Adversarial Causal Bayesian Optimization (ACBO) and introduce the first algorithm for ACBO with bounded regret: Causal Bayesian Optimization with Multiplicative Weights (CBO-MW). Our approach combines a classical online learning strategy with causal modeling of the rewards. To achieve this, it computes optimistic counterfactual reward estimates by propagating uncertainty through the causal graph. We derive regret bounds for CBO-MW that naturally depend on graph-related quantities. We further propose a scalable implementation for the case of combinatorial interventions and submodular rewards. Empirically, CBO-MW outperforms non-causal and non-adversarial Bayesian optimization methods on synthetic environments and environments based on real-word data. Our experiments include a realistic demonstration of how CBO-MW can be used to learn users' demand patterns in a shared mobility system and reposition vehicles in strategic areas.

Amortized Inference for Causal Structure Learning

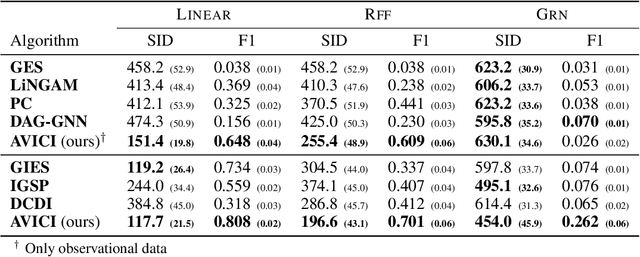
Learning causal structure poses a combinatorial search problem that typically involves evaluating structures using a score or independence test. The resulting search is costly, and designing suitable scores or tests that capture prior knowledge is difficult. In this work, we propose to amortize the process of causal structure learning. Rather than searching over causal structures directly, we train a variational inference model to predict the causal structure from observational/interventional data. Our inference model acquires domain-specific inductive bias for causal discovery solely from data generated by a simulator. This allows us to bypass both the search over graphs and the hand-engineering of suitable score functions. Moreover, the architecture of our inference model is permutation invariant w.r.t. the data points and permutation equivariant w.r.t. the variables, facilitating generalization to significantly larger problem instances than seen during training. On synthetic data and semi-synthetic gene expression data, our models exhibit robust generalization capabilities under substantial distribution shift and significantly outperform existing algorithms, especially in the challenging genomics domain.

Near-Optimal Multi-Perturbation Experimental Design for Causal Structure Learning

Causal structure learning is a key problem in many domains. Causal structures can be learnt by performing experiments on the system of interest. We address the largely unexplored problem of designing experiments that simultaneously intervene on multiple variables. While potentially more informative than the commonly considered single-variable interventions, selecting such interventions is algorithmically much more challenging, due to the doubly-exponential combinatorial search space over sets of composite interventions. In this paper, we develop efficient algorithms for optimizing different objective functions quantifying the informativeness of experiments. By establishing novel submodularity properties of these objectives, we provide approximation guarantees for our algorithms. Our algorithms empirically perform superior to both random interventions and algorithms that only select single-variable interventions.

Combining Parametric and Nonparametric Models for Off-Policy Evaluation

We consider a model-based approach to perform batch off-policy evaluation in reinforcement learning. Our method takes a mixture-of-experts approach to combine parametric and non-parametric models of the environment such that the final value estimate has the least expected error. We do so by first estimating the local accuracy of each model and then using a planner to select which model to use at every time step as to minimize the return error estimate along entire trajectories. Across a variety of domains, our mixture-based approach outperforms the individual models alone as well as state-of-the-art importance sampling-based estimators.