Jonas Rothfuss
Bridging the Sim-to-Real Gap with Bayesian Inference
Mar 25, 2024Abstract:We present SIM-FSVGD for learning robot dynamics from data. As opposed to traditional methods, SIM-FSVGD leverages low-fidelity physical priors, e.g., in the form of simulators, to regularize the training of neural network models. While learning accurate dynamics already in the low data regime, SIM-FSVGD scales and excels also when more data is available. We empirically show that learning with implicit physical priors results in accurate mean model estimation as well as precise uncertainty quantification. We demonstrate the effectiveness of SIM-FSVGD in bridging the sim-to-real gap on a high-performance RC racecar system. Using model-based RL, we demonstrate a highly dynamic parking maneuver with drifting, using less than half the data compared to the state of the art.
Data-Efficient Task Generalization via Probabilistic Model-based Meta Reinforcement Learning
Nov 13, 2023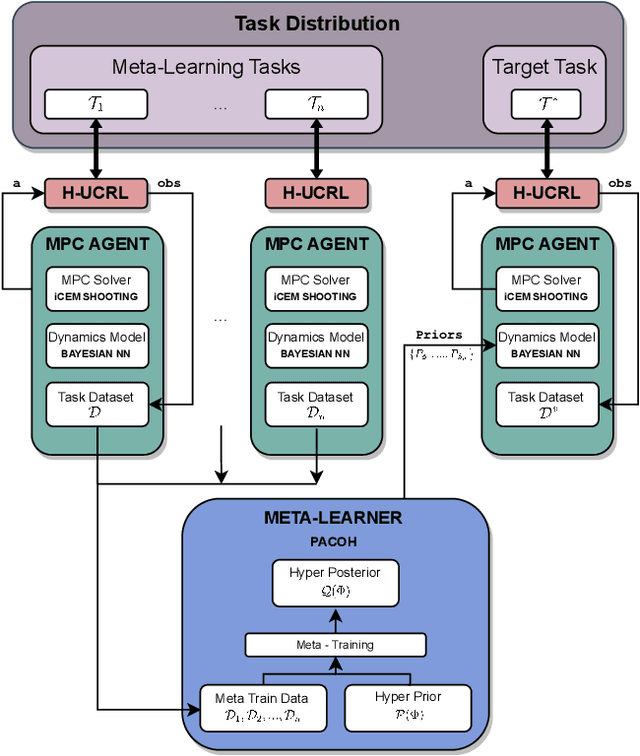


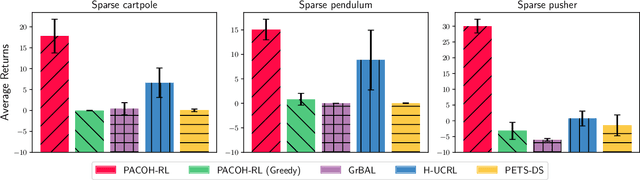
Abstract:We introduce PACOH-RL, a novel model-based Meta-Reinforcement Learning (Meta-RL) algorithm designed to efficiently adapt control policies to changing dynamics. PACOH-RL meta-learns priors for the dynamics model, allowing swift adaptation to new dynamics with minimal interaction data. Existing Meta-RL methods require abundant meta-learning data, limiting their applicability in settings such as robotics, where data is costly to obtain. To address this, PACOH-RL incorporates regularization and epistemic uncertainty quantification in both the meta-learning and task adaptation stages. When facing new dynamics, we use these uncertainty estimates to effectively guide exploration and data collection. Overall, this enables positive transfer, even when access to data from prior tasks or dynamic settings is severely limited. Our experiment results demonstrate that PACOH-RL outperforms model-based RL and model-based Meta-RL baselines in adapting to new dynamic conditions. Finally, on a real robotic car, we showcase the potential for efficient RL policy adaptation in diverse, data-scarce conditions.
Hallucinated Adversarial Control for Conservative Offline Policy Evaluation
Mar 02, 2023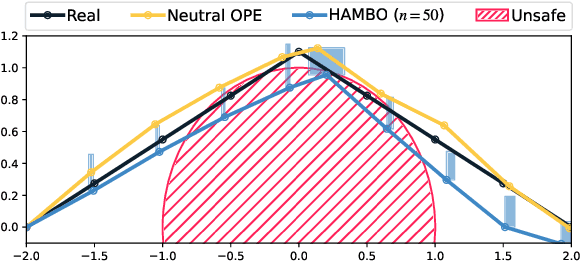
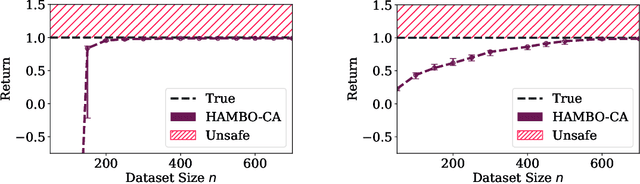
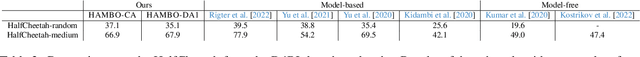
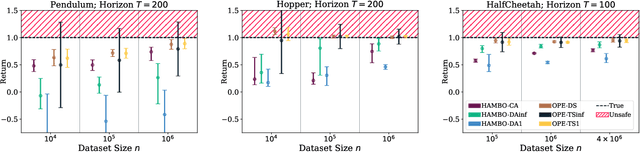
Abstract:We study the problem of conservative off-policy evaluation (COPE) where given an offline dataset of environment interactions, collected by other agents, we seek to obtain a (tight) lower bound on a policy's performance. This is crucial when deciding whether a given policy satisfies certain minimal performance/safety criteria before it can be deployed in the real world. To this end, we introduce HAMBO, which builds on an uncertainty-aware learned model of the transition dynamics. To form a conservative estimate of the policy's performance, HAMBO hallucinates worst-case trajectories that the policy may take, within the margin of the models' epistemic confidence regions. We prove that the resulting COPE estimates are valid lower bounds, and, under regularity conditions, show their convergence to the true expected return. Finally, we discuss scalable variants of our approach based on Bayesian Neural Networks and empirically demonstrate that they yield reliable and tight lower bounds in various continuous control environments.
PAC-Bayesian Meta-Learning: From Theory to Practice
Nov 14, 2022Abstract:Meta-Learning aims to accelerate the learning on new tasks by acquiring useful inductive biases from related data sources. In practice, the number of tasks available for meta-learning is often small. Yet, most of the existing approaches rely on an abundance of meta-training tasks, making them prone to overfitting. How to regularize the meta-learner to ensure generalization to unseen tasks, is a central question in the literature. We provide a theoretical analysis using the PAC-Bayesian framework and derive the first bound for meta-learners with unbounded loss functions. Crucially, our bounds allow us to derive the PAC-optimal hyper-posterior (PACOH) - the closed-form-solution of the PAC-Bayesian meta-learning problem, thereby avoiding the reliance on nested optimization, giving rise to an optimization problem amenable to standard variational methods that scale well. Our experiments show that, when instantiating the PACOH with Gaussian processes and Bayesian Neural Networks as base learners, the resulting methods are more scalable, and yield state-of-the-art performance, both in terms of predictive accuracy and the quality of uncertainty estimates. Finally, thanks to the principled treatment of uncertainty, our meta-learners can also be successfully employed for sequential decision problems.
Instance-Dependent Generalization Bounds via Optimal Transport
Nov 07, 2022Abstract:Existing generalization bounds fail to explain crucial factors that drive generalization of modern neural networks. Since such bounds often hold uniformly over all parameters, they suffer from over-parametrization, and fail to account for the strong inductive bias of initialization and stochastic gradient descent. As an alternative, we propose a novel optimal transport interpretation of the generalization problem. This allows us to derive instance-dependent generalization bounds that depend on the local Lipschitz regularity of the earned prediction function in the data space. Therefore, our bounds are agnostic to the parametrization of the model and work well when the number of training samples is much smaller than the number of parameters. With small modifications, our approach yields accelerated rates for data on low-dimensional manifolds, and guarantees under distribution shifts. We empirically analyze our generalization bounds for neural networks, showing that the bound values are meaningful and capture the effect of popular regularization methods during training.
Lifelong Bandit Optimization: No Prior and No Regret
Oct 27, 2022Abstract:In practical applications, machine learning algorithms are often repeatedly applied to problems with similar structure over and over again. We focus on solving a sequence of bandit optimization tasks and develop LiBO, an algorithm which adapts to the environment by learning from past experience and becoming more sample-efficient in the process. We assume a kernelized structure where the kernel is unknown but shared across all tasks. LiBO sequentially meta-learns a kernel that approximates the true kernel and simultaneously solves the incoming tasks with the latest kernel estimate. Our algorithm can be paired with any kernelized bandit algorithm and guarantees oracle optimal performance, meaning that as more tasks are solved, the regret of LiBO on each task converges to the regret of the bandit algorithm with oracle knowledge of the true kernel. Naturally, if paired with a sublinear bandit algorithm, LiBO yields a sublinear lifelong regret. We also show that direct access to the data from each task is not necessary for attaining sublinear regret. The lifelong problem can thus be solved in a federated manner, while keeping the data of each task private.
MARS: Meta-Learning as Score Matching in the Function Space
Oct 24, 2022



Abstract:Meta-learning aims to extract useful inductive biases from a set of related datasets. In Bayesian meta-learning, this is typically achieved by constructing a prior distribution over neural network parameters. However, specifying families of computationally viable prior distributions over the high-dimensional neural network parameters is difficult. As a result, existing approaches resort to meta-learning restrictive diagonal Gaussian priors, severely limiting their expressiveness and performance. To circumvent these issues, we approach meta-learning through the lens of functional Bayesian neural network inference, which views the prior as a stochastic process and performs inference in the function space. Specifically, we view the meta-training tasks as samples from the data-generating process and formalize meta-learning as empirically estimating the law of this stochastic process. Our approach can seamlessly acquire and represent complex prior knowledge by meta-learning the score function of the data-generating process marginals instead of parameter space priors. In a comprehensive benchmark, we demonstrate that our method achieves state-of-the-art performance in terms of predictive accuracy and substantial improvements in the quality of uncertainty estimates.
Meta-Learning Priors for Safe Bayesian Optimization
Oct 03, 2022
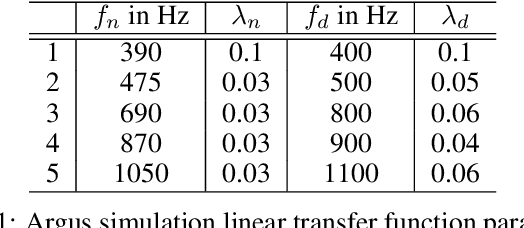
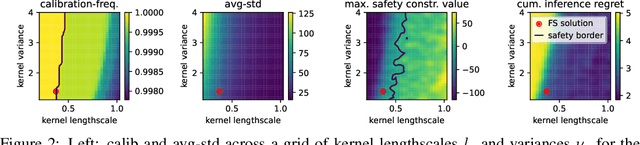

Abstract:In robotics, optimizing controller parameters under safety constraints is an important challenge. Safe Bayesian optimization (BO) quantifies uncertainty in the objective and constraints to safely guide exploration in such settings. Hand-designing a suitable probabilistic model can be challenging, however. In the presence of unknown safety constraints, it is crucial to choose reliable model hyper-parameters to avoid safety violations. Here, we propose a data-driven approach to this problem by meta-learning priors for safe BO from offline data. We build on a meta-learning algorithm, F-PACOH, capable of providing reliable uncertainty quantification in settings of data scarcity. As core contribution, we develop a novel framework for choosing safety-compliant priors in a data-riven manner via empirical uncertainty metrics and a frontier search algorithm. On benchmark functions and a high-precision motion system, we demonstrate that our meta-learned priors accelerate the convergence of safe BO approaches while maintaining safety.
BaCaDI: Bayesian Causal Discovery with Unknown Interventions
Jun 03, 2022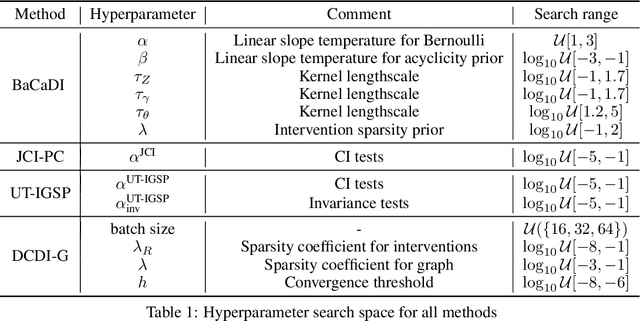
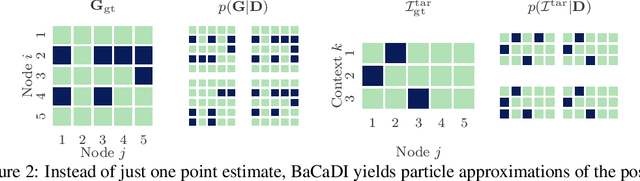
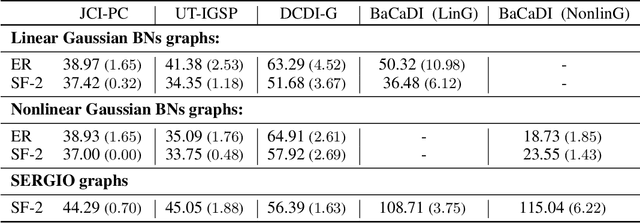
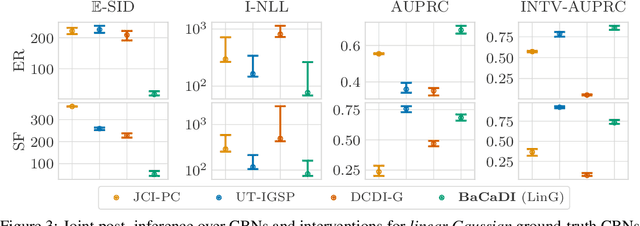
Abstract:Learning causal structures from observation and experimentation is a central task in many domains. For example, in biology, recent advances allow us to obtain single-cell expression data under multiple interventions such as drugs or gene knockouts. However, a key challenge is that often the targets of the interventions are uncertain or unknown. Thus, standard causal discovery methods can no longer be used. To fill this gap, we propose a Bayesian framework (BaCaDI) for discovering the causal structure that underlies data generated under various unknown experimental/interventional conditions. BaCaDI is fully differentiable and operates in the continuous space of latent probabilistic representations of both causal structures and interventions. This enables us to approximate complex posteriors via gradient-based variational inference and to reason about the epistemic uncertainty in the predicted structure. In experiments on synthetic causal discovery tasks and simulated gene-expression data, BaCaDI outperforms related methods in identifying causal structures and intervention targets. Finally, we demonstrate that, thanks to its rigorous Bayesian approach, our method provides well-calibrated uncertainty estimates.
Amortized Inference for Causal Structure Learning
May 25, 2022
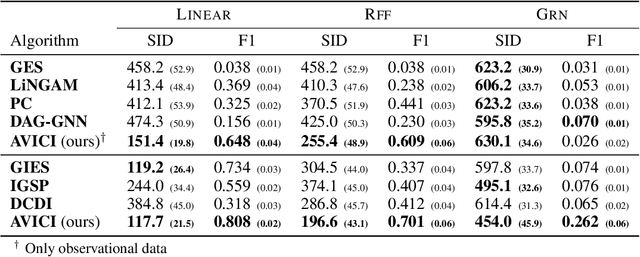


Abstract:Learning causal structure poses a combinatorial search problem that typically involves evaluating structures using a score or independence test. The resulting search is costly, and designing suitable scores or tests that capture prior knowledge is difficult. In this work, we propose to amortize the process of causal structure learning. Rather than searching over causal structures directly, we train a variational inference model to predict the causal structure from observational/interventional data. Our inference model acquires domain-specific inductive bias for causal discovery solely from data generated by a simulator. This allows us to bypass both the search over graphs and the hand-engineering of suitable score functions. Moreover, the architecture of our inference model is permutation invariant w.r.t. the data points and permutation equivariant w.r.t. the variables, facilitating generalization to significantly larger problem instances than seen during training. On synthetic data and semi-synthetic gene expression data, our models exhibit robust generalization capabilities under substantial distribution shift and significantly outperform existing algorithms, especially in the challenging genomics domain.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge