Generative Intervention Models for Causal Perturbation Modeling

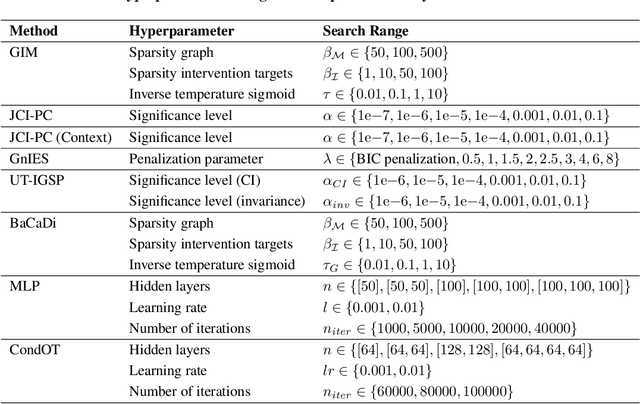
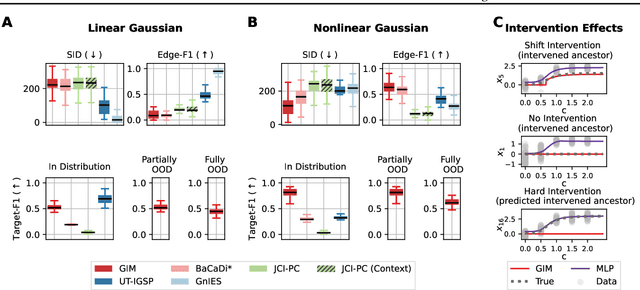
We consider the problem of predicting perturbation effects via causal models. In many applications, it is a priori unknown which mechanisms of a system are modified by an external perturbation, even though the features of the perturbation are available. For example, in genomics, some properties of a drug may be known, but not their causal effects on the regulatory pathways of cells. We propose a generative intervention model (GIM) that learns to map these perturbation features to distributions over atomic interventions in a jointly-estimated causal model. Contrary to prior approaches, this enables us to predict the distribution shifts of unseen perturbation features while gaining insights about their mechanistic effects in the underlying data-generating process. On synthetic data and scRNA-seq drug perturbation data, GIMs achieve robust out-of-distribution predictions on par with unstructured approaches, while effectively inferring the underlying perturbation mechanisms, often better than other causal inference methods.

Standardizing Structural Causal Models

Synthetic datasets generated by structural causal models (SCMs) are commonly used for benchmarking causal structure learning algorithms. However, the variances and pairwise correlations in SCM data tend to increase along the causal ordering. Several popular algorithms exploit these artifacts, possibly leading to conclusions that do not generalize to real-world settings. Existing metrics like $\operatorname{Var}$-sortability and $\operatorname{R^2}$-sortability quantify these patterns, but they do not provide tools to remedy them. To address this, we propose internally-standardized structural causal models (iSCMs), a modification of SCMs that introduces a standardization operation at each variable during the generative process. By construction, iSCMs are not $\operatorname{Var}$-sortable, and as we show experimentally, not $\operatorname{R^2}$-sortable either for commonly-used graph families. Moreover, contrary to the post-hoc standardization of data generated by standard SCMs, we prove that linear iSCMs are less identifiable from prior knowledge on the weights and do not collapse to deterministic relationships in large systems, which may make iSCMs a useful model in causal inference beyond the benchmarking problem studied here.

Causal Modeling with Stationary Diffusions

We develop a novel approach towards causal inference. Rather than structural equations over a causal graph, we learn stochastic differential equations (SDEs) whose stationary densities model a system's behavior under interventions. These stationary diffusion models do not require the formalism of causal graphs, let alone the common assumption of acyclicity. We show that in several cases, they generalize to unseen interventions on their variables, often better than classical approaches. Our inference method is based on a new theoretical result that expresses a stationarity condition on the diffusion's generator in a reproducing kernel Hilbert space. The resulting kernel deviation from stationarity (KDS) is an objective function of independent interest.

Active Bayesian Causal Inference

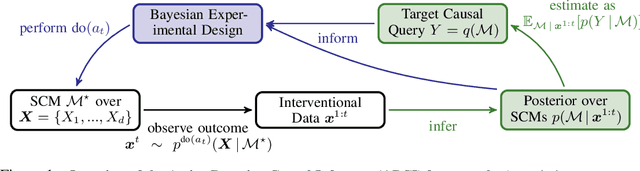
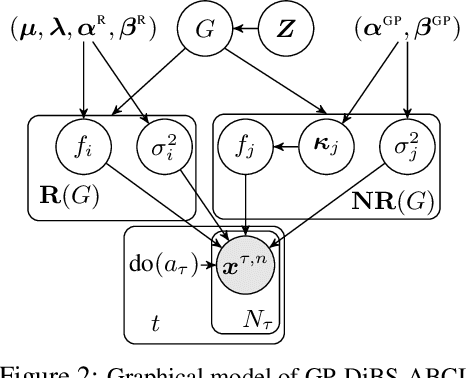
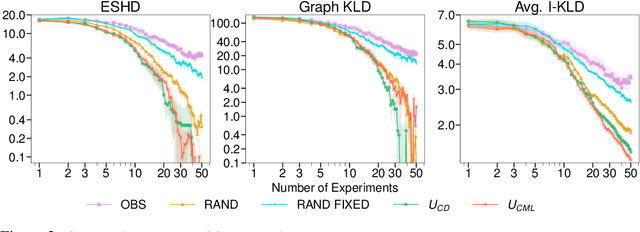
Causal discovery and causal reasoning are classically treated as separate and consecutive tasks: one first infers the causal graph, and then uses it to estimate causal effects of interventions. However, such a two-stage approach is uneconomical, especially in terms of actively collected interventional data, since the causal query of interest may not require a fully-specified causal model. From a Bayesian perspective, it is also unnatural, since a causal query (e.g., the causal graph or some causal effect) can be viewed as a latent quantity subject to posterior inference -- other unobserved quantities that are not of direct interest (e.g., the full causal model) ought to be marginalized out in this process and contribute to our epistemic uncertainty. In this work, we propose Active Bayesian Causal Inference (ABCI), a fully-Bayesian active learning framework for integrated causal discovery and reasoning, which jointly infers a posterior over causal models and queries of interest. In our approach to ABCI, we focus on the class of causally-sufficient, nonlinear additive noise models, which we model using Gaussian processes. We sequentially design experiments that are maximally informative about our target causal query, collect the corresponding interventional data, and update our beliefs to choose the next experiment. Through simulations, we demonstrate that our approach is more data-efficient than several baselines that only focus on learning the full causal graph. This allows us to accurately learn downstream causal queries from fewer samples while providing well-calibrated uncertainty estimates for the quantities of interest.

BaCaDI: Bayesian Causal Discovery with Unknown Interventions

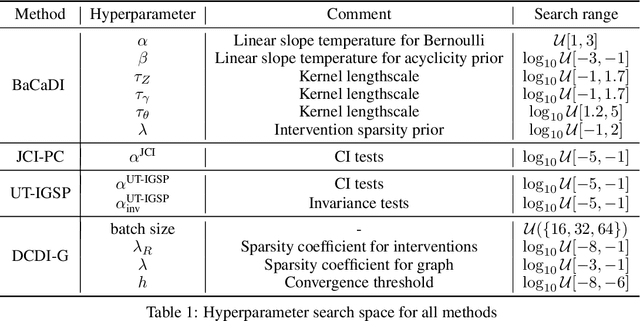
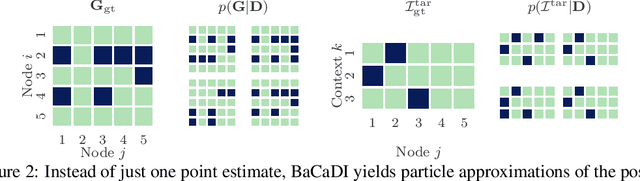
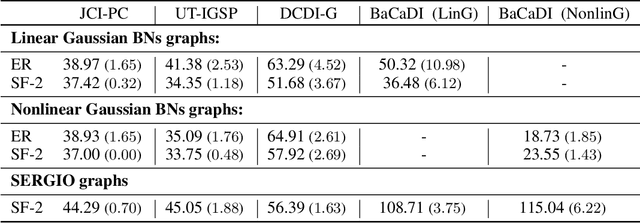
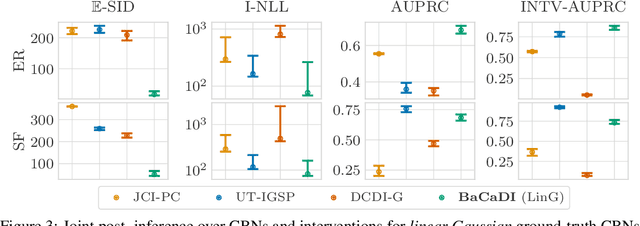
Learning causal structures from observation and experimentation is a central task in many domains. For example, in biology, recent advances allow us to obtain single-cell expression data under multiple interventions such as drugs or gene knockouts. However, a key challenge is that often the targets of the interventions are uncertain or unknown. Thus, standard causal discovery methods can no longer be used. To fill this gap, we propose a Bayesian framework (BaCaDI) for discovering the causal structure that underlies data generated under various unknown experimental/interventional conditions. BaCaDI is fully differentiable and operates in the continuous space of latent probabilistic representations of both causal structures and interventions. This enables us to approximate complex posteriors via gradient-based variational inference and to reason about the epistemic uncertainty in the predicted structure. In experiments on synthetic causal discovery tasks and simulated gene-expression data, BaCaDI outperforms related methods in identifying causal structures and intervention targets. Finally, we demonstrate that, thanks to its rigorous Bayesian approach, our method provides well-calibrated uncertainty estimates.

Amortized Inference for Causal Structure Learning

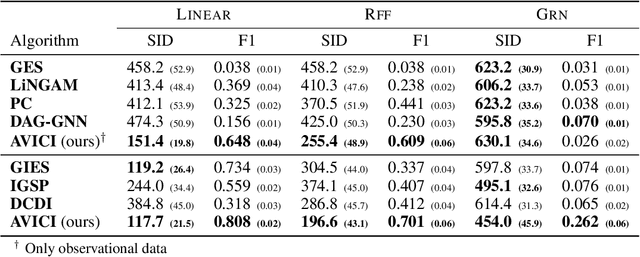
Learning causal structure poses a combinatorial search problem that typically involves evaluating structures using a score or independence test. The resulting search is costly, and designing suitable scores or tests that capture prior knowledge is difficult. In this work, we propose to amortize the process of causal structure learning. Rather than searching over causal structures directly, we train a variational inference model to predict the causal structure from observational/interventional data. Our inference model acquires domain-specific inductive bias for causal discovery solely from data generated by a simulator. This allows us to bypass both the search over graphs and the hand-engineering of suitable score functions. Moreover, the architecture of our inference model is permutation invariant w.r.t. the data points and permutation equivariant w.r.t. the variables, facilitating generalization to significantly larger problem instances than seen during training. On synthetic data and semi-synthetic gene expression data, our models exhibit robust generalization capabilities under substantial distribution shift and significantly outperform existing algorithms, especially in the challenging genomics domain.

Group Testing under Superspreading Dynamics

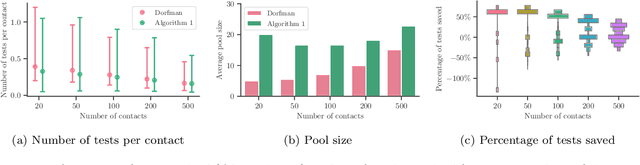
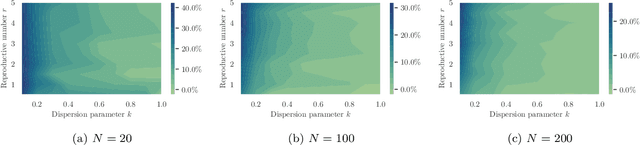
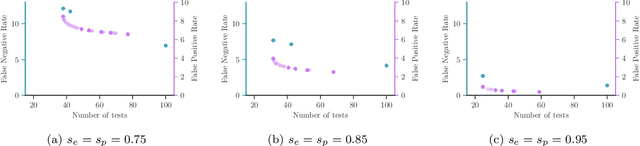
Testing is recommended for all close contacts of confirmed COVID-19 patients. However, existing group testing methods are oblivious to the circumstances of contagion provided by contact tracing. Here, we build upon a well-known semi-adaptive pool testing method, Dorfman's method with imperfect tests, and derive a simple group testing method based on dynamic programming that is specifically designed to use the information provided by contact tracing. Experiments using a variety of reproduction numbers and dispersion levels, including those estimated in the context of the COVID-19 pandemic, show that the pools found using our method result in a significantly lower number of tests than those found using standard Dorfman's method, especially when the number of contacts of an infected individual is small. Moreover, our results show that our method can be more beneficial when the secondary infections are highly overdispersed.

DiBS: Differentiable Bayesian Structure Learning

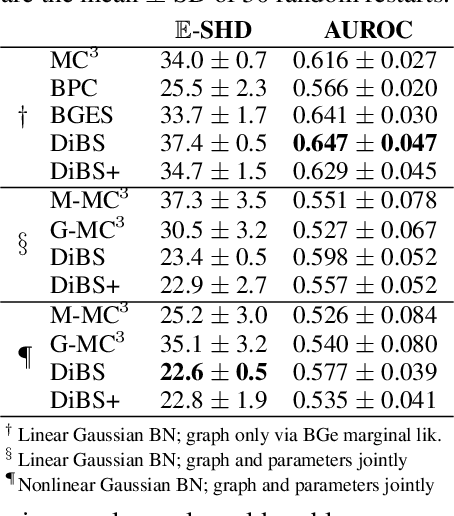
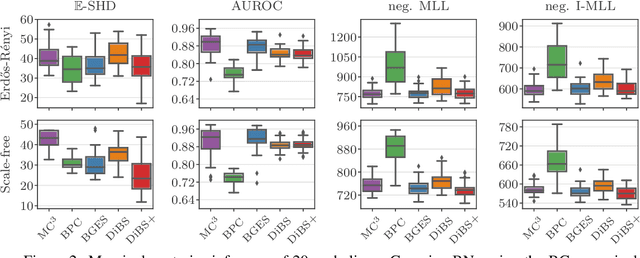
Bayesian structure learning allows inferring Bayesian network structure from data while reasoning about the epistemic uncertainty -- a key element towards enabling active causal discovery and designing interventions in real world systems. In this work, we propose a general, fully differentiable framework for Bayesian structure learning (DiBS) that operates in the continuous space of a latent probabilistic graph representation. Building on recent advances in variational inference, we use DiBS to devise an efficient method for approximating posteriors over structural models. Contrary to existing work, DiBS is agnostic to the form of the local conditional distributions and allows for joint posterior inference of both the graph structure and the conditional distribution parameters. This makes our method directly applicable to posterior inference of nonstandard Bayesian network models, e.g., with nonlinear dependencies encoded by neural networks. In evaluations on simulated and real-world data, DiBS significantly outperforms related approaches to joint posterior inference.

Incorporating Interpretable Output Constraints in Bayesian Neural Networks

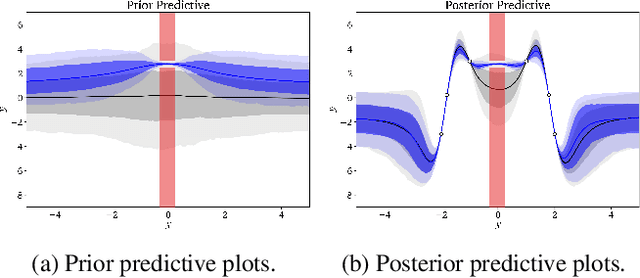
Domains where supervised models are deployed often come with task-specific constraints, such as prior expert knowledge on the ground-truth function, or desiderata like safety and fairness. We introduce a novel probabilistic framework for reasoning with such constraints and formulate a prior that enables us to effectively incorporate them into Bayesian neural networks (BNNs), including a variant that can be amortized over tasks. The resulting Output-Constrained BNN (OC-BNN) is fully consistent with the Bayesian framework for uncertainty quantification and is amenable to black-box inference. Unlike typical BNN inference in uninterpretable parameter space, OC-BNNs widen the range of functional knowledge that can be incorporated, especially for model users without expertise in machine learning. We demonstrate the efficacy of OC-BNNs on real-world datasets, spanning multiple domains such as healthcare, criminal justice, and credit scoring.

A Spatiotemporal Epidemic Model to Quantify the Effects of Contact Tracing, Testing, and Containment

Motivated by the current COVID-19 outbreak, we introduce a novel epidemic model based on marked temporal point processes that is specifically designed to make fine-grained spatiotemporal predictions about the course of the disease in a population. Our model can make use and benefit from data gathered by a variety of contact tracing technologies and it can quantify the effects that different testing and tracing strategies, social distancing measures, and business restrictions may have on the course of the disease. Building on our model, we use Bayesian optimization to estimate the risk of exposure of each individual at the sites they visit, the percentage of symptomatic individuals, and the difference in transmission rate between asymptomatic and symptomatic individuals from historical longitudinal testing data. Experiments using real COVID-19 data and mobility patterns from T\"{u}bingen, a town in the southwest of Germany, demonstrate that our model can be used to quantify the effects of tracing, testing, and containment strategies at an unprecedented spatiotemporal resolution. To facilitate research and informed policy-making, particularly in the context of the current COVID-19 outbreak, we are releasing an open-source implementation of our framework at https://github.com/covid19-model.