DiBS: Differentiable Bayesian Structure Learning

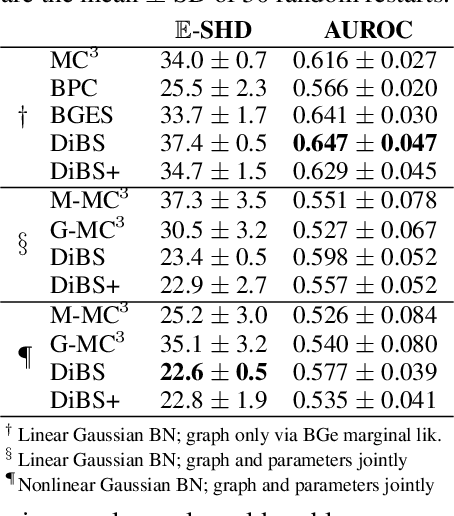
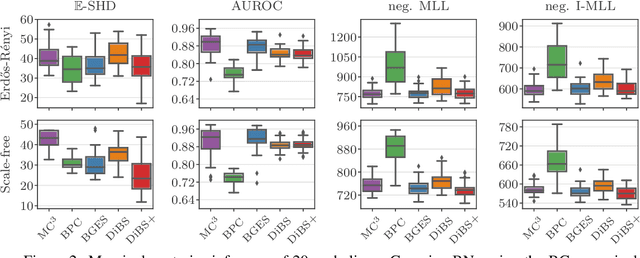
Bayesian structure learning allows inferring Bayesian network structure from data while reasoning about the epistemic uncertainty -- a key element towards enabling active causal discovery and designing interventions in real world systems. In this work, we propose a general, fully differentiable framework for Bayesian structure learning (DiBS) that operates in the continuous space of a latent probabilistic graph representation. Building on recent advances in variational inference, we use DiBS to devise an efficient method for approximating posteriors over structural models. Contrary to existing work, DiBS is agnostic to the form of the local conditional distributions and allows for joint posterior inference of both the graph structure and the conditional distribution parameters. This makes our method directly applicable to posterior inference of nonstandard Bayesian network models, e.g., with nonlinear dependencies encoded by neural networks. In evaluations on simulated and real-world data, DiBS significantly outperforms related approaches to joint posterior inference.