Stratis Tsirtsis
Test-Time Compute Games
Jan 29, 2026Abstract:Test-time compute has emerged as a promising strategy to enhance the reasoning abilities of large language models (LLMs). However, this strategy has in turn increased how much users pay cloud-based providers offering LLM-as-a-service, since providers charge users for the amount of test-time compute they use to generate an output. In our work, we show that the market of LLM-as-a-service is socially inefficient: providers have a financial incentive to increase the amount of test-time compute, even if this increase contributes little to the quality of the outputs. To address this inefficiency, we introduce a reverse second-price auction mechanism where providers bid their offered price and (expected) quality for the opportunity to serve a user, and users pay proportionally to the marginal value generated by the winning provider relative to the second-highest bidder. To illustrate and complement our theoretical results, we conduct experiments with multiple instruct models from the $\texttt{Llama}$ and $\texttt{Qwen}$ families, as well as reasoning models distilled from $\texttt{DeepSeek-R1}$, on math and science benchmark datasets.
Canonical Autoregressive Generation
Jun 06, 2025Abstract:State of the art large language models are trained using large amounts of tokens derived from raw text using what is called a tokenizer. Crucially, the tokenizer determines the (token) vocabulary a model will use during inference as well as, in principle, the (token) language. This is because, while the token vocabulary may allow for different tokenizations of a string, the tokenizer always maps the string to only one of these tokenizations--the canonical tokenization. However, multiple lines of empirical evidence suggest that large language models do not always generate canonical token sequences, and this comes with several negative consequences. In this work, we first show that, to generate a canonical token sequence, a model needs to generate (partial) canonical token sequences at each step of the autoregressive generation process underpinning its functioning. Building upon this theoretical result, we introduce canonical sampling, a simple and efficient sampling method that precludes a given model from generating non-canonical token sequences. Further, we also show that, in comparison with standard sampling, the distribution of token sequences generated using canonical sampling is provably closer to the true distribution of token sequences used during training.
Is Your LLM Overcharging You? Tokenization, Transparency, and Incentives
May 27, 2025Abstract:State-of-the-art large language models require specialized hardware and substantial energy to operate. As a consequence, cloud-based services that provide access to large language models have become very popular. In these services, the price users pay for an output provided by a model depends on the number of tokens the model uses to generate it -- they pay a fixed price per token. In this work, we show that this pricing mechanism creates a financial incentive for providers to strategize and misreport the (number of) tokens a model used to generate an output, and users cannot prove, or even know, whether a provider is overcharging them. However, we also show that, if an unfaithful provider is obliged to be transparent about the generative process used by the model, misreporting optimally without raising suspicion is hard. Nevertheless, as a proof-of-concept, we introduce an efficient heuristic algorithm that allows providers to significantly overcharge users without raising suspicion, highlighting the vulnerability of users under the current pay-per-token pricing mechanism. Further, to completely eliminate the financial incentive to strategize, we introduce a simple incentive-compatible token pricing mechanism. Under this mechanism, the price users pay for an output provided by a model depends on the number of characters of the output -- they pay a fixed price per character. Along the way, to illustrate and complement our theoretical results, we conduct experiments with several large language models from the $\texttt{Llama}$, $\texttt{Gemma}$ and $\texttt{Ministral}$ families, and input prompts from the LMSYS Chatbot Arena platform.
Evaluation of Large Language Models via Coupled Token Generation
Feb 03, 2025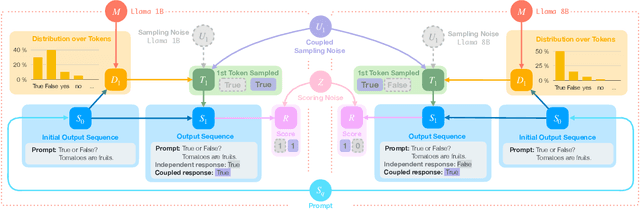
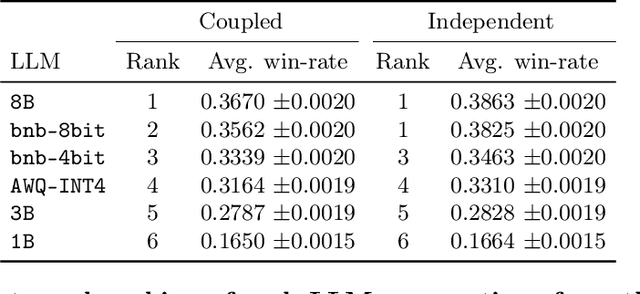
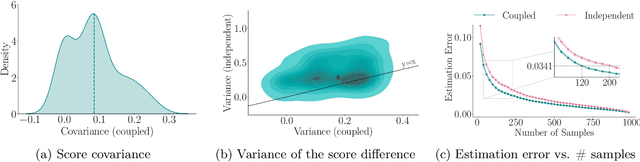
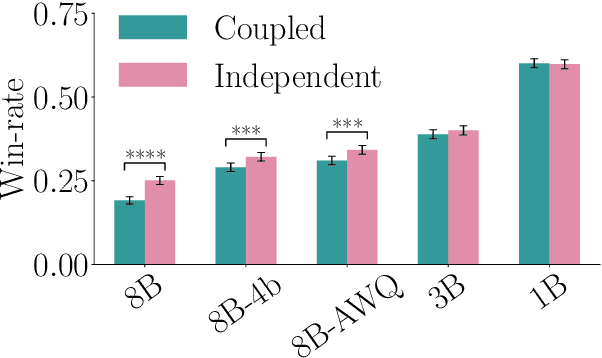
Abstract:State of the art large language models rely on randomization to respond to a prompt. As an immediate consequence, a model may respond differently to the same prompt if asked multiple times. In this work, we argue that the evaluation and ranking of large language models should control for the randomization underpinning their functioning. Our starting point is the development of a causal model for coupled autoregressive generation, which allows different large language models to sample responses with the same source of randomness. Building upon our causal model, we first show that, on evaluations based on benchmark datasets, coupled autoregressive generation leads to the same conclusions as vanilla autoregressive generation but using provably fewer samples. However, we further show that, on evaluations based on (human) pairwise comparisons, coupled and vanilla autoregressive generation can surprisingly lead to different rankings when comparing more than two models, even with an infinite amount of samples. This suggests that the apparent advantage of a model over others in existing evaluation protocols may not be genuine but rather confounded by the randomness inherent to the generation process. To illustrate and complement our theoretical results, we conduct experiments with several large language models from the Llama family. We find that, across multiple knowledge areas from the popular MMLU benchmark dataset, coupled autoregressive generation requires up to 40% fewer samples to reach the same conclusions as vanilla autoregressive generation. Further, using data from the LMSYS Chatbot Arena platform, we find that the win-rates derived from pairwise comparisons by a strong large language model to prompts differ under coupled and vanilla autoregressive generation.
Counterfactual Token Generation in Large Language Models
Sep 25, 2024



Abstract:"Sure, I am happy to generate a story for you: Captain Lyra stood at the helm of her trusty ship, the Maelstrom's Fury, gazing out at the endless sea. [...] Lyra's eyes welled up with tears as she realized the bitter truth - she had sacrificed everything for fleeting riches, and lost the love of her crew, her family, and herself." Although this story, generated by a large language model, is captivating, one may wonder -- how would the story have unfolded if the model had chosen "Captain Maeve" as the protagonist instead? We cannot know. State-of-the-art large language models are stateless -- they maintain no internal memory or state. Given a prompt, they generate a sequence of tokens as an output using an autoregressive process. As a consequence, they cannot reason about counterfactual alternatives to tokens they have generated in the past. In this work, our goal is to enhance them with this functionality. To this end, we develop a causal model of token generation that builds upon the Gumbel-Max structural causal model. Our model allows any large language model to perform counterfactual token generation at almost no cost in comparison with vanilla token generation, it is embarrassingly simple to implement, and it does not require any fine-tuning nor prompt engineering. We implement our model on Llama 3 8B-instruct and conduct both qualitative and quantitative analyses of counterfactually generated text. We conclude with a demonstrative application of counterfactual token generation for bias detection, unveiling interesting insights about the model of the world constructed by large language models.
Finding Counterfactually Optimal Action Sequences in Continuous State Spaces
Jun 06, 2023



Abstract:Humans performing tasks that involve taking a series of multiple dependent actions over time often learn from experience by reflecting on specific cases and points in time, where different actions could have led to significantly better outcomes. While recent machine learning methods to retrospectively analyze sequential decision making processes promise to aid decision makers in identifying such cases, they have focused on environments with finitely many discrete states. However, in many practical applications, the state of the environment is inherently continuous in nature. In this paper, we aim to fill this gap. We start by formally characterizing a sequence of discrete actions and continuous states using finite horizon Markov decision processes and a broad class of bijective structural causal models. Building upon this characterization, we formalize the problem of finding counterfactually optimal action sequences and show that, in general, we cannot expect to solve it in polynomial time. Then, we develop a search method based on the $A^*$ algorithm that, under a natural form of Lipschitz continuity of the environment's dynamics, is guaranteed to return the optimal solution to the problem. Experiments on real clinical data show that our method is very efficient in practice, and it has the potential to offer interesting insights for sequential decision making tasks.
On the Within-Group Discrimination of Screening Classifiers
Jan 31, 2023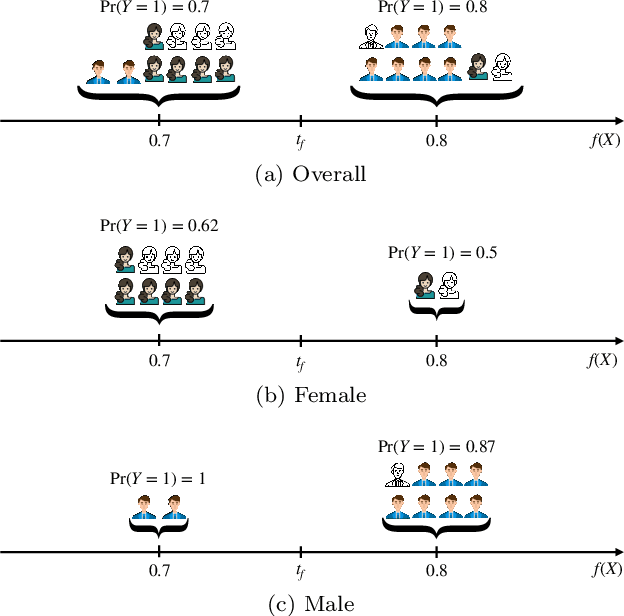
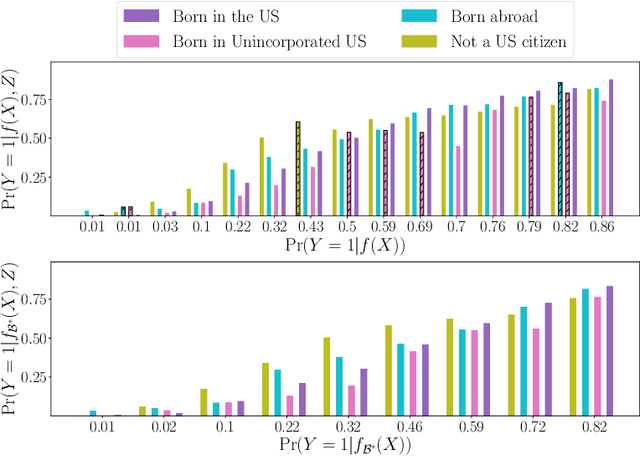
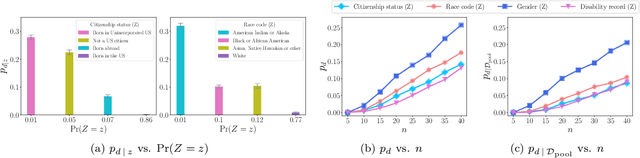
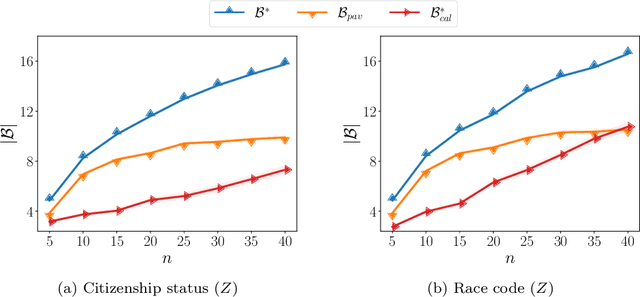
Abstract:Screening classifiers are increasingly used to identify qualified candidates in a variety of selection processes. In this context, it has been recently shown that, if a classifier is calibrated, one can identify the smallest set of candidates which contains, in expectation, a desired number of qualified candidates using a threshold decision rule. This lends support to focusing on calibration as the only requirement for screening classifiers. In this paper, we argue that screening policies that use calibrated classifiers may suffer from an understudied type of within-group discrimination -- they may discriminate against qualified members within demographic groups of interest. Further, we argue that this type of discrimination can be avoided if classifiers satisfy within-group monotonicity, a natural monotonicity property within each of the groups. Then, we introduce an efficient post-processing algorithm based on dynamic programming to minimally modify a given calibrated classifier so that its probability estimates satisfy within-group monotonicity. We validate our algorithm using US Census survey data and show that within-group monotonicity can be often achieved at a small cost in terms of prediction granularity and shortlist size.
Counterfactual Explanations in Sequential Decision Making Under Uncertainty
Jul 06, 2021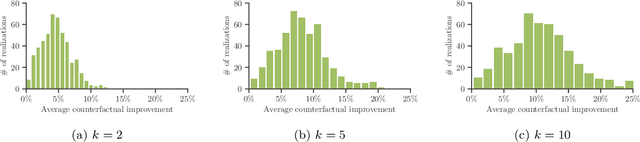
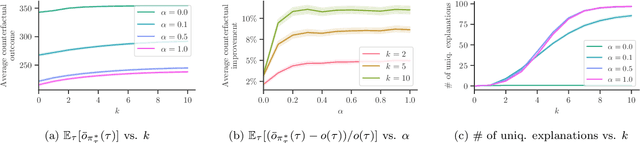
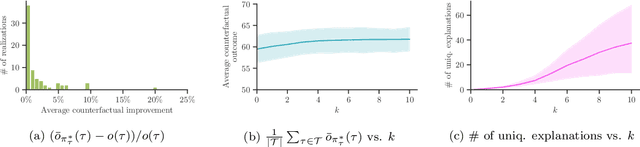

Abstract:Methods to find counterfactual explanations have predominantly focused on one step decision making processes. In this work, we initiate the development of methods to find counterfactual explanations for decision making processes in which multiple, dependent actions are taken sequentially over time. We start by formally characterizing a sequence of actions and states using finite horizon Markov decision processes and the Gumbel-Max structural causal model. Building upon this characterization, we formally state the problem of finding counterfactual explanations for sequential decision making processes. In our problem formulation, the counterfactual explanation specifies an alternative sequence of actions differing in at most k actions from the observed sequence that could have led the observed process realization to a better outcome. Then, we introduce a polynomial time algorithm based on dynamic programming to build a counterfactual policy that is guaranteed to always provide the optimal counterfactual explanation on every possible realization of the counterfactual environment dynamics. We validate our algorithm using both synthetic and real data from cognitive behavioral therapy and show that the counterfactual explanations our algorithm finds can provide valuable insights to enhance sequential decision making under uncertainty.
Group Testing under Superspreading Dynamics
Jun 30, 2021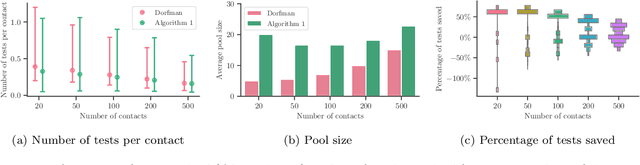
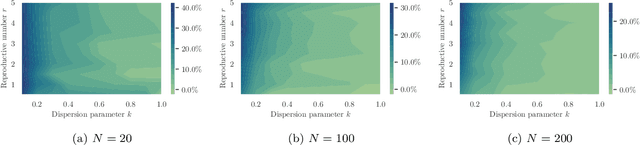
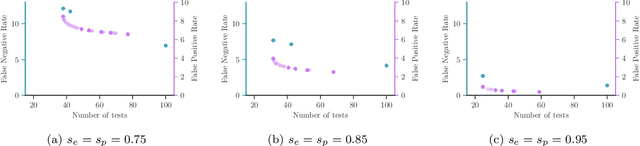
Abstract:Testing is recommended for all close contacts of confirmed COVID-19 patients. However, existing group testing methods are oblivious to the circumstances of contagion provided by contact tracing. Here, we build upon a well-known semi-adaptive pool testing method, Dorfman's method with imperfect tests, and derive a simple group testing method based on dynamic programming that is specifically designed to use the information provided by contact tracing. Experiments using a variety of reproduction numbers and dispersion levels, including those estimated in the context of the COVID-19 pandemic, show that the pools found using our method result in a significantly lower number of tests than those found using standard Dorfman's method, especially when the number of contacts of an infected individual is small. Moreover, our results show that our method can be more beneficial when the secondary infections are highly overdispersed.
Bridging Machine Learning and Mechanism Design towards Algorithmic Fairness
Oct 12, 2020Abstract:Decision-making systems increasingly orchestrate our world: how to intervene on the algorithmic components to build fair and equitable systems is therefore a question of utmost importance; one that is substantially complicated by the context-dependent nature of fairness and discrimination. Modern systems incorporate machine-learned predictions in broader decision-making pipelines, implicating concerns like constrained allocation and strategic behavior that are typically thought of as mechanism design problems. Although both machine learning and mechanism design have individually developed frameworks for addressing issues of fairness and equity, in some complex decision-making systems, neither framework is individually sufficient. In this paper, we develop the position that building fair decision-making systems requires overcoming these limitations which, we argue, are inherent to the individual frameworks of machine learning and mechanism design. Our ultimate objective is to build an encompassing framework that cohesively bridges the individual frameworks. We begin to lay the ground work towards achieving this goal by comparing the perspective each individual discipline takes on fair decision-making, teasing out the lessons each field has taught and can teach the other, and highlighting application domains that require a strong collaboration between these disciplines.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge