William Trouleau
A Spatiotemporal Epidemic Model to Quantify the Effects of Contact Tracing, Testing, and Containment
Apr 24, 2020
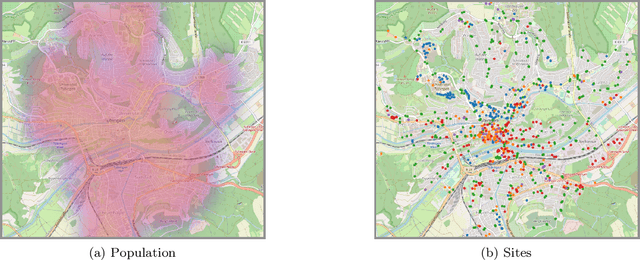

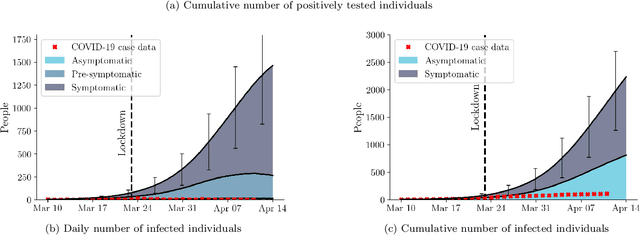
Abstract:Motivated by the current COVID-19 outbreak, we introduce a novel epidemic model based on marked temporal point processes that is specifically designed to make fine-grained spatiotemporal predictions about the course of the disease in a population. Our model can make use and benefit from data gathered by a variety of contact tracing technologies and it can quantify the effects that different testing and tracing strategies, social distancing measures, and business restrictions may have on the course of the disease. Building on our model, we use Bayesian optimization to estimate the risk of exposure of each individual at the sites they visit, the percentage of symptomatic individuals, and the difference in transmission rate between asymptomatic and symptomatic individuals from historical longitudinal testing data. Experiments using real COVID-19 data and mobility patterns from T\"{u}bingen, a town in the southwest of Germany, demonstrate that our model can be used to quantify the effects of tracing, testing, and containment strategies at an unprecedented spatiotemporal resolution. To facilitate research and informed policy-making, particularly in the context of the current COVID-19 outbreak, we are releasing an open-source implementation of our framework at https://github.com/covid19-model.
Learning Hawkes Processes from a Handful of Events
Nov 01, 2019

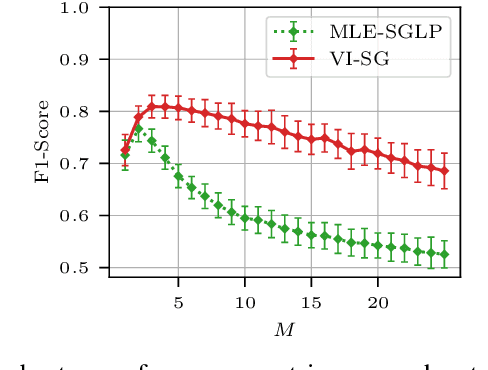
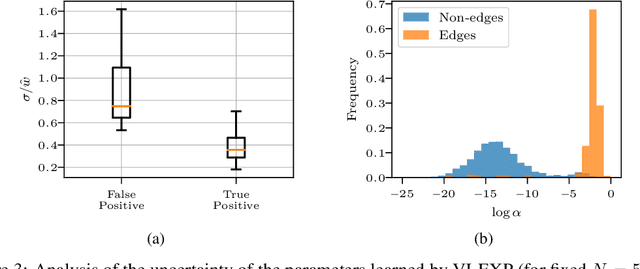
Abstract:Learning the causal-interaction network of multivariate Hawkes processes is a useful task in many applications. Maximum-likelihood estimation is the most common approach to solve the problem in the presence of long observation sequences. However, when only short sequences are available, the lack of data amplifies the risk of overfitting and regularization becomes critical. Due to the challenges of hyper-parameter tuning, state-of-the-art methods only parameterize regularizers by a single shared hyper-parameter, hence limiting the power of representation of the model. To solve both issues, we develop in this work an efficient algorithm based on variational expectation-maximization. Our approach is able to optimize over an extended set of hyper-parameters. It is also able to take into account the uncertainty in the model parameters by learning a posterior distribution over them. Experimental results on both synthetic and real datasets show that our approach significantly outperforms state-of-the-art methods under short observation sequences.
Stochastic Optimal Control of Epidemic Processes in Networks
Oct 30, 2018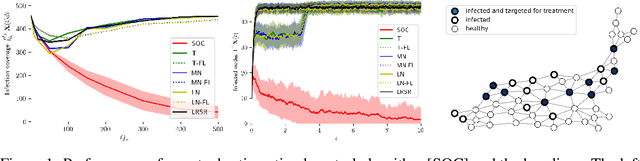
Abstract:We approach the development of models and control strategies of susceptible-infected-susceptible (SIS) epidemic processes from the perspective of marked temporal point processes and stochastic optimal control of stochastic differential equations (SDEs) with jumps. In contrast to previous work, this novel perspective is particularly well-suited to make use of fine-grained data about disease outbreaks, and it lets us overcome the shortcomings of current control strategies. Our control strategy resorts to treatment intensities to determine who to treat and when to do so, to minimize the amount of infected individuals over time. Preliminary experiments with synthetic data show that our control strategy consistently outperforms several alternatives. Looking into the future, we believe our methodology provides a promising step towards the development of practical data-driven control strategies of epidemic processes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge