Optimizing Through Change: Bounds and Recommendations for Time-Varying Bayesian Optimization Algorithms

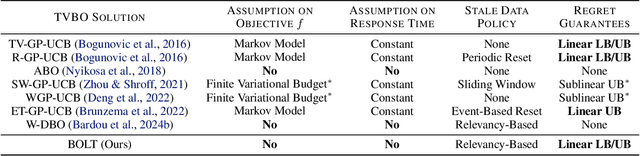
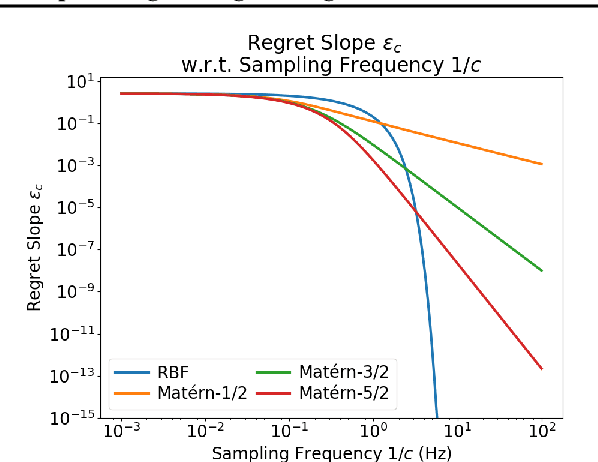
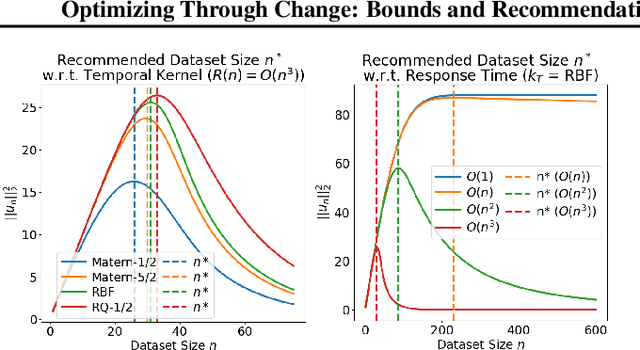
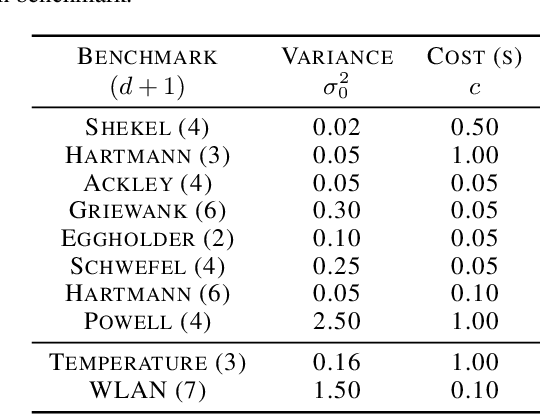
Time-Varying Bayesian Optimization (TVBO) is the go-to framework for optimizing a time-varying, expensive, noisy black-box function. However, most of the solutions proposed so far either rely on unrealistic assumptions on the nature of the objective function or do not offer any theoretical guarantees. We propose the first analysis that asymptotically bounds the cumulative regret of TVBO algorithms under mild and realistic assumptions only. In particular, we provide an algorithm-independent lower regret bound and an upper regret bound that holds for a large class of TVBO algorithms. Based on this analysis, we formulate recommendations for TVBO algorithms and show how an algorithm (BOLT) that follows them performs better than the state-of-the-art of TVBO through experiments on synthetic and real-world problems.

Complexity of Minimizing Projected-Gradient-Dominated Functions with Stochastic First-order Oracles

This work investigates the performance limits of projected stochastic first-order methods for minimizing functions under the $(\alpha,\tau,\mathcal{X})$-projected-gradient-dominance property, that asserts the sub-optimality gap $F(\mathbf{x})-\min_{\mathbf{x}'\in \mathcal{X}}F(\mathbf{x}')$ is upper-bounded by $\tau\cdot\|\mathcal{G}_{\eta,\mathcal{X}}(\mathbf{x})\|^{\alpha}$ for some $\alpha\in[1,2)$ and $\tau>0$ and $\mathcal{G}_{\eta,\mathcal{X}}(\mathbf{x})$ is the projected-gradient mapping with $\eta>0$ as a parameter. For non-convex functions, we show that the complexity lower bound of querying a batch smooth first-order stochastic oracle to obtain an $\epsilon$-global-optimum point is $\Omega(\epsilon^{-{2}/{\alpha}})$. Furthermore, we show that a projected variance-reduced first-order algorithm can obtain the upper complexity bound of $\mathcal{O}(\epsilon^{-{2}/{\alpha}})$, matching the lower bound. For convex functions, we establish a complexity lower bound of $\Omega(\log(1/\epsilon)\cdot\epsilon^{-{2}/{\alpha}})$ for minimizing functions under a local version of gradient-dominance property, which also matches the upper complexity bound of accelerated stochastic subgradient methods.

Fast Proxy Experiment Design for Causal Effect Identification

Identifying causal effects is a key problem of interest across many disciplines. The two long-standing approaches to estimate causal effects are observational and experimental (randomized) studies. Observational studies can suffer from unmeasured confounding, which may render the causal effects unidentifiable. On the other hand, direct experiments on the target variable may be too costly or even infeasible to conduct. A middle ground between these two approaches is to estimate the causal effect of interest through proxy experiments, which are conducted on variables with a lower cost to intervene on compared to the main target. Akbari et al. [2022] studied this setting and demonstrated that the problem of designing the optimal (minimum-cost) experiment for causal effect identification is NP-complete and provided a naive algorithm that may require solving exponentially many NP-hard problems as a sub-routine in the worst case. In this work, we provide a few reformulations of the problem that allow for designing significantly more efficient algorithms to solve it as witnessed by our extensive simulations. Additionally, we study the closely-related problem of designing experiments that enable us to identify a given effect through valid adjustments sets.

Why the Metric Backbone Preserves Community Structure

The metric backbone of a weighted graph is the union of all-pairs shortest paths. It is obtained by removing all edges $(u,v)$ that are not the shortest path between $u$ and $v$. In networks with well-separated communities, the metric backbone tends to preserve many inter-community edges, because these edges serve as bridges connecting two communities, but tends to delete many intra-community edges because the communities are dense. This suggests that the metric backbone would dilute or destroy the community structure of the network. However, this is not borne out by prior empirical work, which instead showed that the metric backbone of real networks preserves the community structure of the original network well. In this work, we analyze the metric backbone of a broad class of weighted random graphs with communities, and we formally prove the robustness of the community structure with respect to the deletion of all the edges that are not in the metric backbone. An empirical comparison of several graph sparsification techniques confirms our theoretical finding and shows that the metric backbone is an efficient sparsifier in the presence of communities.

This Too Shall Pass: Removing Stale Observations in Dynamic Bayesian Optimization

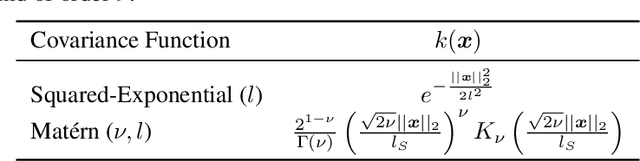
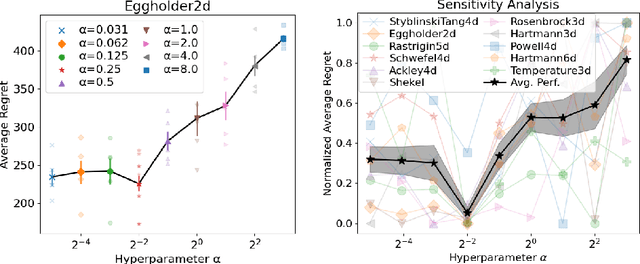
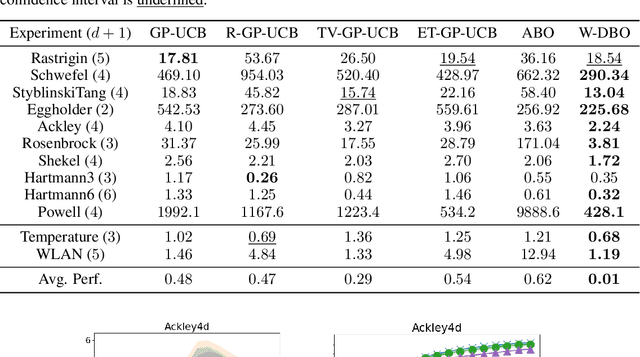
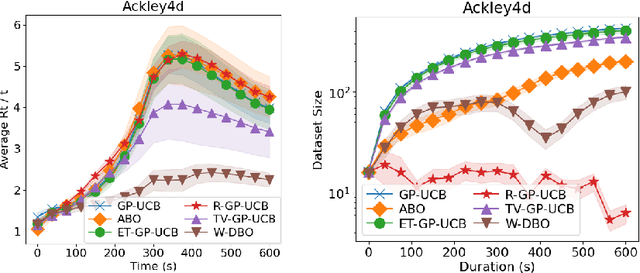
Bayesian Optimization (BO) has proven to be very successful at optimizing a static, noisy, costly-to-evaluate black-box function $f : \mathcal{S} \to \mathbb{R}$. However, optimizing a black-box which is also a function of time (i.e., a dynamic function) $f : \mathcal{S} \times \mathcal{T} \to \mathbb{R}$ remains a challenge, since a dynamic Bayesian Optimization (DBO) algorithm has to keep track of the optimum over time. This changes the nature of the optimization problem in at least three aspects: (i) querying an arbitrary point in $\mathcal{S} \times \mathcal{T}$ is impossible, (ii) past observations become less and less relevant for keeping track of the optimum as time goes by and (iii) the DBO algorithm must have a high sampling frequency so it can collect enough relevant observations to keep track of the optimum through time. In this paper, we design a Wasserstein distance-based criterion able to quantify the relevancy of an observation with respect to future predictions. Then, we leverage this criterion to build W-DBO, a DBO algorithm able to remove irrelevant observations from its dataset on the fly, thus maintaining simultaneously a good predictive performance and a high sampling frequency, even in continuous-time optimization tasks with unknown horizon. Numerical experiments establish the superiority of W-DBO, which outperforms state-of-the-art methods by a comfortable margin.

Universal Lower Bounds and Optimal Rates: Achieving Minimax Clustering Error in Sub-Exponential Mixture Models

Clustering is a pivotal challenge in unsupervised machine learning and is often investigated through the lens of mixture models. The optimal error rate for recovering cluster labels in Gaussian and sub-Gaussian mixture models involves ad hoc signal-to-noise ratios. Simple iterative algorithms, such as Lloyd's algorithm, attain this optimal error rate. In this paper, we first establish a universal lower bound for the error rate in clustering any mixture model, expressed through a Chernoff divergence, a more versatile measure of model information than signal-to-noise ratios. We then demonstrate that iterative algorithms attain this lower bound in mixture models with sub-exponential tails, notably emphasizing location-scale mixtures featuring Laplace-distributed errors. Additionally, for datasets better modelled by Poisson or Negative Binomial mixtures, we study mixture models whose distributions belong to an exponential family. In such mixtures, we establish that Bregman hard clustering, a variant of Lloyd's algorithm employing a Bregman divergence, is rate optimal.

Differences Between Hard and Noisy-labeled Samples: An Empirical Study

Extracting noisy or incorrectly labeled samples from a labeled dataset with hard/difficult samples is an important yet under-explored topic. Two general and often independent lines of work exist, one focuses on addressing noisy labels, and another deals with hard samples. However, when both types of data are present, most existing methods treat them equally, which results in a decline in the overall performance of the model. In this paper, we first design various synthetic datasets with custom hardness and noisiness levels for different samples. Our proposed systematic empirical study enables us to better understand the similarities and more importantly the differences between hard-to-learn samples and incorrectly-labeled samples. These controlled experiments pave the way for the development of methods that distinguish between hard and noisy samples. Through our study, we introduce a simple yet effective metric that filters out noisy-labeled samples while keeping the hard samples. We study various data partitioning methods in the presence of label noise and observe that filtering out noisy samples from hard samples with this proposed metric results in the best datasets as evidenced by the high test accuracy achieved after models are trained on the filtered datasets. We demonstrate this for both our created synthetic datasets and for datasets with real-world label noise. Furthermore, our proposed data partitioning method significantly outperforms other methods when employed within a semi-supervised learning framework.

When Does Bottom-up Beat Top-down in Hierarchical Community Detection?

Hierarchical clustering of networks consists in finding a tree of communities, such that lower levels of the hierarchy reveal finer-grained community structures. There are two main classes of algorithms tackling this problem. Divisive ($\textit{top-down}$) algorithms recursively partition the nodes into two communities, until a stopping rule indicates that no further split is needed. In contrast, agglomerative ($\textit{bottom-up}$) algorithms first identify the smallest community structure and then repeatedly merge the communities using a $\textit{linkage}$ method. In this article, we establish theoretical guarantees for the recovery of the hierarchical tree and community structure of a Hierarchical Stochastic Block Model by a bottom-up algorithm. We also establish that this bottom-up algorithm attains the information-theoretic threshold for exact recovery at intermediate levels of the hierarchy. Notably, these recovery conditions are less restrictive compared to those existing for top-down algorithms. This shows that bottom-up algorithms extend the feasible region for achieving exact recovery at intermediate levels. Numerical experiments on both synthetic and real data sets confirm the superiority of bottom-up algorithms over top-down algorithms. We also observe that top-down algorithms can produce dendrograms with inversions. These findings contribute to a better understanding of hierarchical clustering techniques and their applications in network analysis.

Relaxing the Additivity Constraints in Decentralized No-Regret High-Dimensional Bayesian Optimization

Bayesian Optimization (BO) is typically used to optimize an unknown function $f$ that is noisy and costly to evaluate, by exploiting an acquisition function that must be maximized at each optimization step. Although provably asymptotically optimal BO algorithms are efficient at optimizing low-dimensional functions, scaling them to high-dimensional spaces remains an open research problem, often tackled by assuming an additive structure for $f$. However, such algorithms introduce additional restrictive assumptions on the additive structure that reduce their applicability domain. In this paper, we relax the restrictive assumptions on the additive structure of $f$, at the expense of weakening the maximization guarantees of the acquisition function, and we address the over-exploration problem for decentralized BO algorithms. To these ends, we propose DuMBO, an asymptotically optimal decentralized BO algorithm that achieves very competitive performance against state-of-the-art BO algorithms, especially when the additive structure of $f$ does not exist or comprises high-dimensional factors.

Leveraging Unlabeled Data to Track Memorization

Deep neural networks may easily memorize noisy labels present in real-world data, which degrades their ability to generalize. It is therefore important to track and evaluate the robustness of models against noisy label memorization. We propose a metric, called susceptibility, to gauge such memorization for neural networks. Susceptibility is simple and easy to compute during training. Moreover, it does not require access to ground-truth labels and it only uses unlabeled data. We empirically show the effectiveness of our metric in tracking memorization on various architectures and datasets and provide theoretical insights into the design of the susceptibility metric. Finally, we show through extensive experiments on datasets with synthetic and real-world label noise that one can utilize susceptibility and the overall training accuracy to distinguish models that maintain a low memorization on the training set and generalize well to unseen clean data.