Differences Between Hard and Noisy-labeled Samples: An Empirical Study

Extracting noisy or incorrectly labeled samples from a labeled dataset with hard/difficult samples is an important yet under-explored topic. Two general and often independent lines of work exist, one focuses on addressing noisy labels, and another deals with hard samples. However, when both types of data are present, most existing methods treat them equally, which results in a decline in the overall performance of the model. In this paper, we first design various synthetic datasets with custom hardness and noisiness levels for different samples. Our proposed systematic empirical study enables us to better understand the similarities and more importantly the differences between hard-to-learn samples and incorrectly-labeled samples. These controlled experiments pave the way for the development of methods that distinguish between hard and noisy samples. Through our study, we introduce a simple yet effective metric that filters out noisy-labeled samples while keeping the hard samples. We study various data partitioning methods in the presence of label noise and observe that filtering out noisy samples from hard samples with this proposed metric results in the best datasets as evidenced by the high test accuracy achieved after models are trained on the filtered datasets. We demonstrate this for both our created synthetic datasets and for datasets with real-world label noise. Furthermore, our proposed data partitioning method significantly outperforms other methods when employed within a semi-supervised learning framework.

Leveraging Unlabeled Data to Track Memorization

Deep neural networks may easily memorize noisy labels present in real-world data, which degrades their ability to generalize. It is therefore important to track and evaluate the robustness of models against noisy label memorization. We propose a metric, called susceptibility, to gauge such memorization for neural networks. Susceptibility is simple and easy to compute during training. Moreover, it does not require access to ground-truth labels and it only uses unlabeled data. We empirically show the effectiveness of our metric in tracking memorization on various architectures and datasets and provide theoretical insights into the design of the susceptibility metric. Finally, we show through extensive experiments on datasets with synthetic and real-world label noise that one can utilize susceptibility and the overall training accuracy to distinguish models that maintain a low memorization on the training set and generalize well to unseen clean data.

Disparity Between Batches as a Signal for Early Stopping

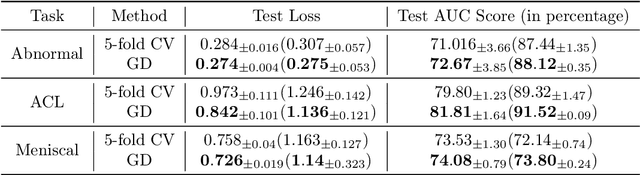
We propose a metric for evaluating the generalization ability of deep neural networks trained with mini-batch gradient descent. Our metric, called gradient disparity, is the $\ell_2$ norm distance between the gradient vectors of two mini-batches drawn from the training set. It is derived from a probabilistic upper bound on the difference between the classification errors over a given mini-batch, when the network is trained on this mini-batch and when the network is trained on another mini-batch of points sampled from the same dataset. We empirically show that gradient disparity is a very promising early-stopping criterion (i) when data is limited, as it uses all the samples for training and (ii) when available data has noisy labels, as it signals overfitting better than the validation data. Furthermore, we show in a wide range of experimental settings that gradient disparity is strongly related to the generalization error between the training and test sets, and that it is also very informative about the level of label noise.

Generalization Comparison of Deep Neural Networks via Output Sensitivity

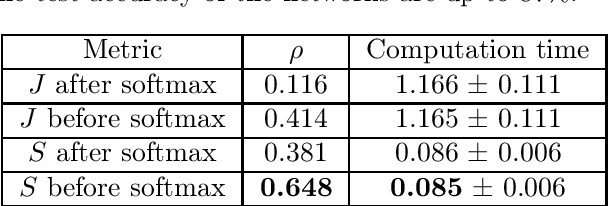
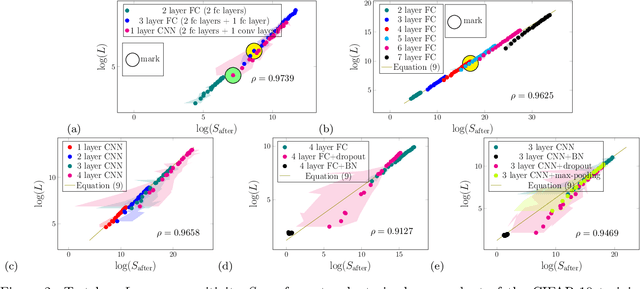
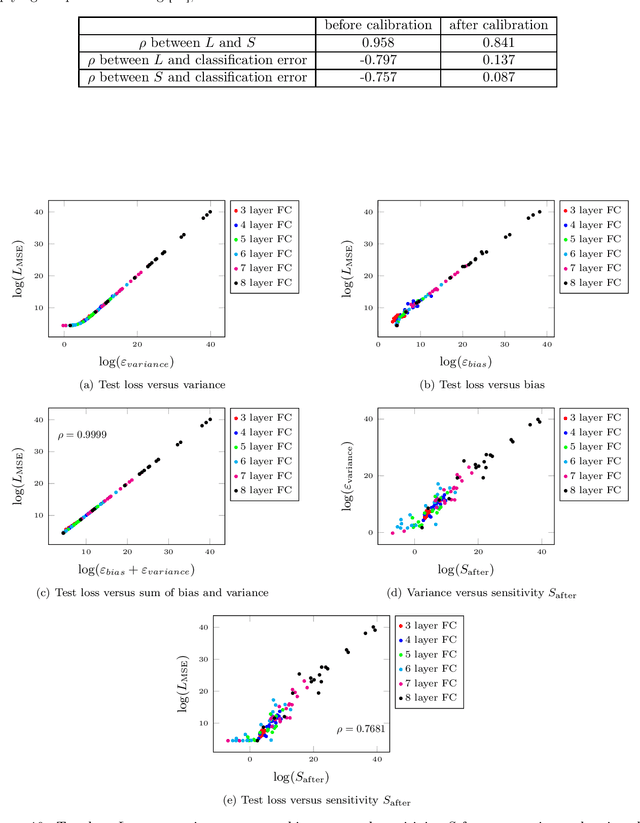
Although recent works have brought some insights into the performance improvement of techniques used in state-of-the-art deep-learning models, more work is needed to understand their generalization properties. We shed light on this matter by linking the loss function to the output's sensitivity to its input. We find a rather strong empirical relation between the output sensitivity and the variance in the bias-variance decomposition of the loss function, which hints on using sensitivity as a metric for comparing the generalization performance of networks, without requiring labeled data. We find that sensitivity is decreased by applying popular methods which improve the generalization performance of the model, such as (1) using a deep network rather than a wide one, (2) adding convolutional layers to baseline classifiers instead of adding fully-connected layers, (3) using batch normalization, dropout and max-pooling, and (4) applying parameter initialization techniques.