Disparity Between Batches as a Signal for Early Stopping

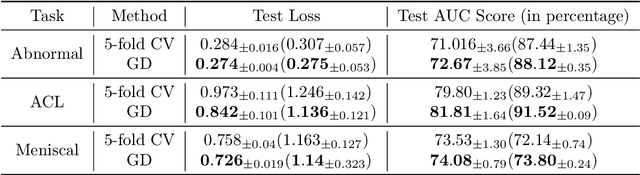
We propose a metric for evaluating the generalization ability of deep neural networks trained with mini-batch gradient descent. Our metric, called gradient disparity, is the $\ell_2$ norm distance between the gradient vectors of two mini-batches drawn from the training set. It is derived from a probabilistic upper bound on the difference between the classification errors over a given mini-batch, when the network is trained on this mini-batch and when the network is trained on another mini-batch of points sampled from the same dataset. We empirically show that gradient disparity is a very promising early-stopping criterion (i) when data is limited, as it uses all the samples for training and (ii) when available data has noisy labels, as it signals overfitting better than the validation data. Furthermore, we show in a wide range of experimental settings that gradient disparity is strongly related to the generalization error between the training and test sets, and that it is also very informative about the level of label noise.