Stylized Structural Patterns for Improved Neural Network Pre-training

Modern deep learning models in computer vision require large datasets of real images, which are difficult to curate and pose privacy and legal concerns, limiting their commercial use. Recent works suggest synthetic data as an alternative, yet models trained with it often underperform. This paper proposes a two-step approach to bridge this gap. First, we propose an improved neural fractal formulation through which we introduce a new class of synthetic data. Second, we propose reverse stylization, a technique that transfers visual features from a small, license-free set of real images onto synthetic datasets, enhancing their effectiveness. We analyze the domain gap between our synthetic datasets and real images using Kernel Inception Distance (KID) and show that our method achieves a significantly lower distributional gap compared to existing synthetic datasets. Furthermore, our experiments across different tasks demonstrate the practical impact of this reduced gap. We show that pretraining the EDM2 diffusion model on our synthetic dataset leads to an 11% reduction in FID during image generation, compared to models trained on existing synthetic datasets, and a 20% decrease in autoencoder reconstruction error, indicating improved performance in data representation. Furthermore, a ViT-S model trained for classification on this synthetic data achieves over a 10% improvement in ImageNet-100 accuracy. Our work opens up exciting possibilities for training practical models when sufficiently large real training sets are not available.

Guidance in the Frequency Domain Enables High-Fidelity Sampling at Low CFG Scales

Classifier-free guidance (CFG) has become an essential component of modern conditional diffusion models. Although highly effective in practice, the underlying mechanisms by which CFG enhances quality, detail, and prompt alignment are not fully understood. We present a novel perspective on CFG by analyzing its effects in the frequency domain, showing that low and high frequencies have distinct impacts on generation quality. Specifically, low-frequency guidance governs global structure and condition alignment, while high-frequency guidance mainly enhances visual fidelity. However, applying a uniform scale across all frequencies -- as is done in standard CFG -- leads to oversaturation and reduced diversity at high scales and degraded visual quality at low scales. Based on these insights, we propose frequency-decoupled guidance (FDG), an effective approach that decomposes CFG into low- and high-frequency components and applies separate guidance strengths to each component. FDG improves image quality at low guidance scales and avoids the drawbacks of high CFG scales by design. Through extensive experiments across multiple datasets and models, we demonstrate that FDG consistently enhances sample fidelity while preserving diversity, leading to improved FID and recall compared to CFG, establishing our method as a plug-and-play alternative to standard classifier-free guidance.

Generalization Comparison of Deep Neural Networks via Output Sensitivity

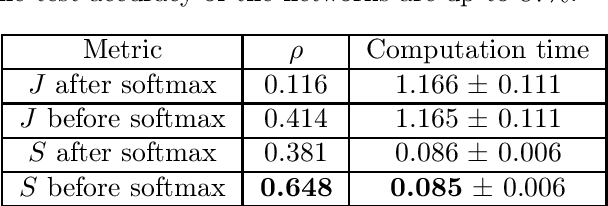
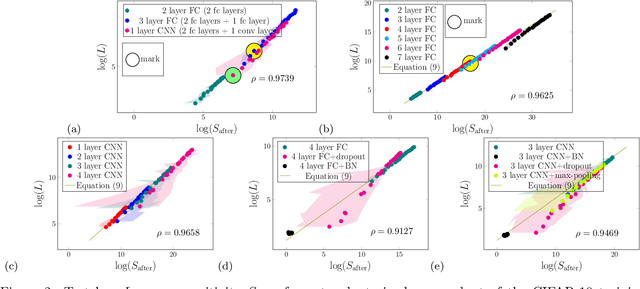
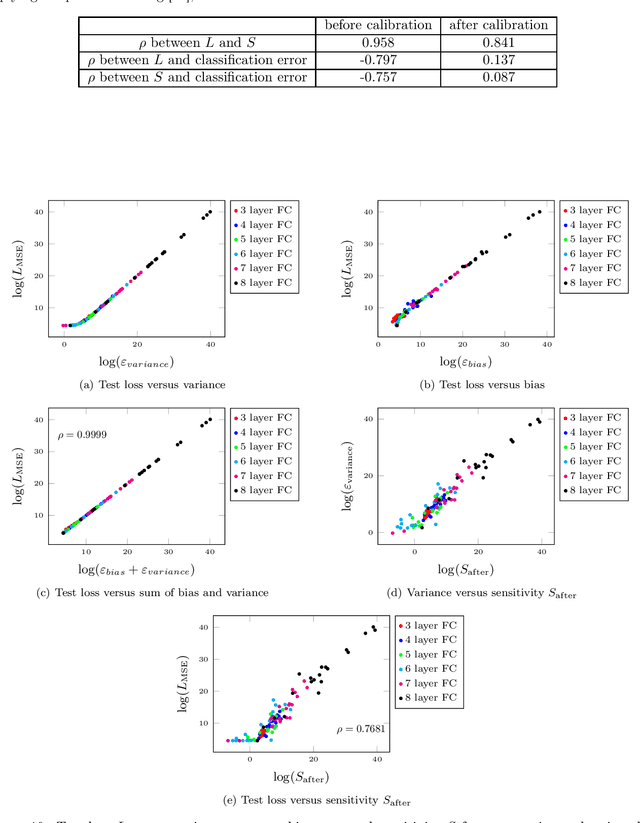
Although recent works have brought some insights into the performance improvement of techniques used in state-of-the-art deep-learning models, more work is needed to understand their generalization properties. We shed light on this matter by linking the loss function to the output's sensitivity to its input. We find a rather strong empirical relation between the output sensitivity and the variance in the bias-variance decomposition of the loss function, which hints on using sensitivity as a metric for comparing the generalization performance of networks, without requiring labeled data. We find that sensitivity is decreased by applying popular methods which improve the generalization performance of the model, such as (1) using a deep network rather than a wide one, (2) adding convolutional layers to baseline classifiers instead of adding fully-connected layers, (3) using batch normalization, dropout and max-pooling, and (4) applying parameter initialization techniques.

Learning Hawkes Processes from a Handful of Events

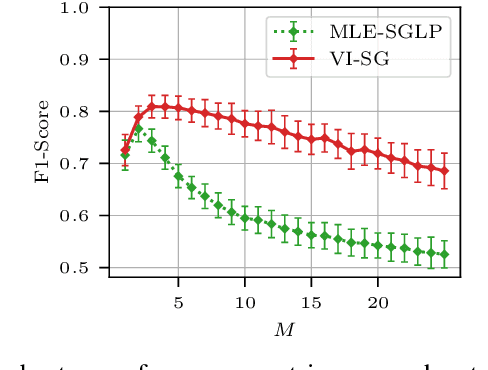
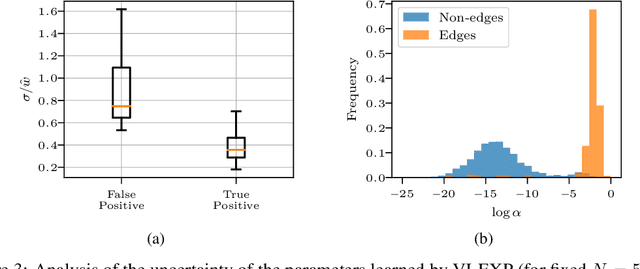
Learning the causal-interaction network of multivariate Hawkes processes is a useful task in many applications. Maximum-likelihood estimation is the most common approach to solve the problem in the presence of long observation sequences. However, when only short sequences are available, the lack of data amplifies the risk of overfitting and regularization becomes critical. Due to the challenges of hyper-parameter tuning, state-of-the-art methods only parameterize regularizers by a single shared hyper-parameter, hence limiting the power of representation of the model. To solve both issues, we develop in this work an efficient algorithm based on variational expectation-maximization. Our approach is able to optimize over an extended set of hyper-parameters. It is also able to take into account the uncertainty in the model parameters by learning a posterior distribution over them. Experimental results on both synthetic and real datasets show that our approach significantly outperforms state-of-the-art methods under short observation sequences.

Augmenting and Tuning Knowledge Graph Embeddings

Knowledge graph embeddings rank among the most successful methods for link prediction in knowledge graphs, i.e., the task of completing an incomplete collection of relational facts. A downside of these models is their strong sensitivity to model hyperparameters, in particular regularizers, which have to be extensively tuned to reach good performance [Kadlec et al., 2017]. We propose an efficient method for large scale hyperparameter tuning by interpreting these models in a probabilistic framework. After a model augmentation that introduces per-entity hyperparameters, we use a variational expectation-maximization approach to tune thousands of such hyperparameters with minimal additional cost. Our approach is agnostic to details of the model and results in a new state of the art in link prediction on standard benchmark data.

An Algorithmic Framework to Control Bias in Bandit-based Personalization

Personalization is pervasive in the online space as it leads to higher efficiency and revenue by allowing the most relevant content to be served to each user. However, recent studies suggest that personalization methods can propagate societal or systemic biases and polarize opinions; this has led to calls for regulatory mechanisms and algorithms to combat bias and inequality. Algorithmically, bandit optimization has enjoyed great success in learning user preferences and personalizing content or feeds accordingly. We propose an algorithmic framework that allows for the possibility to control bias or discrimination in such bandit-based personalization. Our model allows for the specification of general fairness constraints on the sensitive types of the content that can be displayed to a user. The challenge, however, is to come up with a scalable and low regret algorithm for the constrained optimization problem that arises. Our main technical contribution is a provably fast and low-regret algorithm for the fairness-constrained bandit optimization problem. Our proofs crucially leverage the special structure of our problem. Experiments on synthetic and real-world data sets show that our algorithmic framework can control bias with only a minor loss to revenue.

Stochastic Dual Coordinate Descent with Bandit Sampling

Coordinate descent methods minimize a cost function by updating a single decision variable (corresponding to one coordinate) at a time. Ideally, one would update the decision variable that yields the largest marginal decrease in the cost function. However, finding this coordinate would require checking all of them, which is not computationally practical. We instead propose a new adaptive method for coordinate descent. First, we define a lower bound on the decrease of the cost function when a coordinate is updated and, instead of calculating this lower bound for all coordinates, we use a multi-armed bandit algorithm to learn which coordinates result in the largest marginal decrease while simultaneously performing coordinate descent. We show that our approach improves the convergence of the coordinate methods (including parallel versions) both theoretically and experimentally.

Stochastic Optimization with Bandit Sampling

Many stochastic optimization algorithms work by estimating the gradient of the cost function on the fly by sampling datapoints uniformly at random from a training set. However, the estimator might have a large variance, which inadvertently slows down the convergence rate of the algorithms. One way to reduce this variance is to sample the datapoints from a carefully selected non-uniform distribution. In this work, we propose a novel non-uniform sampling approach that uses the multi-armed bandit framework. Theoretically, we show that our algorithm asymptotically approximates the optimal variance within a factor of 3. Empirically, we show that using this datapoint-selection technique results in a significant reduction in the convergence time and variance of several stochastic optimization algorithms such as SGD, SVRG and SAGA. This approach for sampling datapoints is general, and can be used in conjunction with any algorithm that uses an unbiased gradient estimation -- we expect it to have broad applicability beyond the specific examples explored in this work.