A Mathematical Framework for AI-Human Integration in Work

The rapid rise of Generative AI (GenAI) tools has sparked debate over their role in complementing or replacing human workers across job contexts. We present a mathematical framework that models jobs, workers, and worker-job fit, introducing a novel decomposition of skills into decision-level and action-level subskills to reflect the complementary strengths of humans and GenAI. We analyze how changes in subskill abilities affect job success, identifying conditions for sharp transitions in success probability. We also establish sufficient conditions under which combining workers with complementary subskills significantly outperforms relying on a single worker. This explains phenomena such as productivity compression, where GenAI assistance yields larger gains for lower-skilled workers. We demonstrate the framework' s practicality using data from O*NET and Big-Bench Lite, aligning real-world data with our model via subskill-division methods. Our results highlight when and how GenAI complements human skills, rather than replacing them.

Efficient Diffusion Models for Symmetric Manifolds

We introduce a framework for designing efficient diffusion models for $d$-dimensional symmetric-space Riemannian manifolds, including the torus, sphere, special orthogonal group and unitary group. Existing manifold diffusion models often depend on heat kernels, which lack closed-form expressions and require either $d$ gradient evaluations or exponential-in-$d$ arithmetic operations per training step. We introduce a new diffusion model for symmetric manifolds with a spatially-varying covariance, allowing us to leverage a projection of Euclidean Brownian motion to bypass heat kernel computations. Our training algorithm minimizes a novel efficient objective derived via Ito's Lemma, allowing each step to run in $O(1)$ gradient evaluations and nearly-linear-in-$d$ ($O(d^{1.19})$) arithmetic operations, reducing the gap between diffusions on symmetric manifolds and Euclidean space. Manifold symmetries ensure the diffusion satisfies an "average-case" Lipschitz condition, enabling accurate and efficient sample generation. Empirically, our model outperforms prior methods in training speed and improves sample quality on synthetic datasets on the torus, special orthogonal group, and unitary group.

Private Low-Rank Approximation for Covariance Matrices, Dyson Brownian Motion, and Eigenvalue-Gap Bounds for Gaussian Perturbations

We consider the problem of approximating a $d \times d$ covariance matrix $M$ with a rank-$k$ matrix under $(\varepsilon,\delta)$-differential privacy. We present and analyze a complex variant of the Gaussian mechanism and obtain upper bounds on the Frobenius norm of the difference between the matrix output by this mechanism and the best rank-$k$ approximation to $M$. Our analysis provides improvements over previous bounds, particularly when the spectrum of $M$ satisfies natural structural assumptions. The novel insight is to view the addition of Gaussian noise to a matrix as a continuous-time matrix Brownian motion. This viewpoint allows us to track the evolution of eigenvalues and eigenvectors of the matrix, which are governed by stochastic differential equations discovered by Dyson. These equations enable us to upper bound the Frobenius distance between the best rank-$k$ approximation of $M$ and that of a Gaussian perturbation of $M$ as an integral that involves inverse eigenvalue gaps of the stochastically evolving matrix, as opposed to a sum of perturbation bounds obtained via Davis-Kahan-type theorems. Subsequently, again using the Dyson Brownian motion viewpoint, we show that the eigenvalues of the matrix $M$ perturbed by Gaussian noise have large gaps with high probability. These results also contribute to the analysis of low-rank approximations under average-case perturbations, and to an understanding of eigenvalue gaps for random matrices, both of which may be of independent interest.

Centralized Selection with Preferences in the Presence of Biases

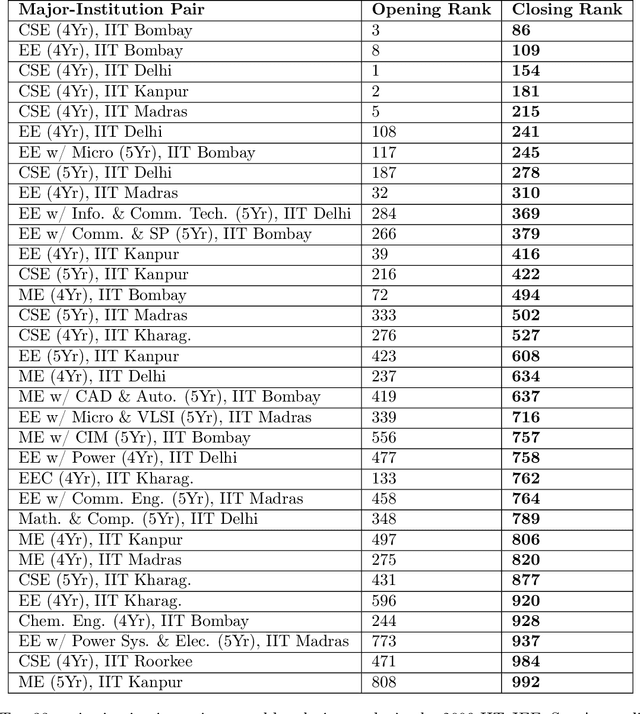
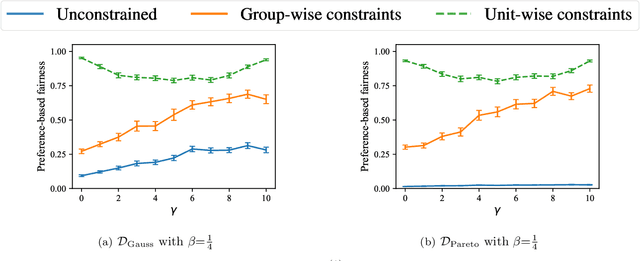
This paper considers the scenario in which there are multiple institutions, each with a limited capacity for candidates, and candidates, each with preferences over the institutions. A central entity evaluates the utility of each candidate to the institutions, and the goal is to select candidates for each institution in a way that maximizes utility while also considering the candidates' preferences. The paper focuses on the setting in which candidates are divided into multiple groups and the observed utilities of candidates in some groups are biased--systematically lower than their true utilities. The first result is that, in these biased settings, prior algorithms can lead to selections with sub-optimal true utility and significant discrepancies in the fraction of candidates from each group that get their preferred choices. Subsequently, an algorithm is presented along with proof that it produces selections that achieve near-optimal group fairness with respect to preferences while also nearly maximizing the true utility under distributional assumptions. Further, extensive empirical validation of these results in real-world and synthetic settings, in which the distributional assumptions may not hold, are presented.

Faster Sampling from Log-Concave Densities over Polytopes via Efficient Linear Solvers

We consider the problem of sampling from a log-concave distribution $\pi(\theta) \propto e^{-f(\theta)}$ constrained to a polytope $K:=\{\theta \in \mathbb{R}^d: A\theta \leq b\}$, where $A\in \mathbb{R}^{m\times d}$ and $b \in \mathbb{R}^m$.The fastest-known algorithm \cite{mangoubi2022faster} for the setting when $f$ is $O(1)$-Lipschitz or $O(1)$-smooth runs in roughly $O(md \times md^{\omega -1})$ arithmetic operations, where the $md^{\omega -1}$ term arises because each Markov chain step requires computing a matrix inversion and determinant (here $\omega \approx 2.37$ is the matrix multiplication constant). We present a nearly-optimal implementation of this Markov chain with per-step complexity which is roughly the number of non-zero entries of $A$ while the number of Markov chain steps remains the same. The key technical ingredients are 1) to show that the matrices that arise in this Dikin walk change slowly, 2) to deploy efficient linear solvers that can leverage this slow change to speed up matrix inversion by using information computed in previous steps, and 3) to speed up the computation of the determinantal term in the Metropolis filter step via a randomized Taylor series-based estimator.

Bias in Evaluation Processes: An Optimization-Based Model

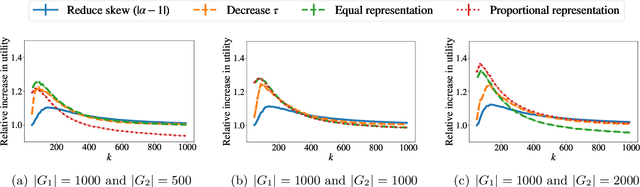
Biases with respect to socially-salient attributes of individuals have been well documented in evaluation processes used in settings such as admissions and hiring. We view such an evaluation process as a transformation of a distribution of the true utility of an individual for a task to an observed distribution and model it as a solution to a loss minimization problem subject to an information constraint. Our model has two parameters that have been identified as factors leading to biases: the resource-information trade-off parameter in the information constraint and the risk-averseness parameter in the loss function. We characterize the distributions that arise from our model and study the effect of the parameters on the observed distribution. The outputs of our model enrich the class of distributions that can be used to capture variation across groups in the observed evaluations. We empirically validate our model by fitting real-world datasets and use it to study the effect of interventions in a downstream selection task. These results contribute to an understanding of the emergence of bias in evaluation processes and provide tools to guide the deployment of interventions to mitigate biases.

Private Covariance Approximation and Eigenvalue-Gap Bounds for Complex Gaussian Perturbations

We consider the problem of approximating a $d \times d$ covariance matrix $M$ with a rank-$k$ matrix under $(\varepsilon,\delta)$-differential privacy. We present and analyze a complex variant of the Gaussian mechanism and show that the Frobenius norm of the difference between the matrix output by this mechanism and the best rank-$k$ approximation to $M$ is bounded by roughly $\tilde{O}(\sqrt{kd})$, whenever there is an appropriately large gap between the $k$'th and the $k+1$'th eigenvalues of $M$. This improves on previous work that requires that the gap between every pair of top-$k$ eigenvalues of $M$ is at least $\sqrt{d}$ for a similar bound. Our analysis leverages the fact that the eigenvalues of complex matrix Brownian motion repel more than in the real case, and uses Dyson's stochastic differential equations governing the evolution of its eigenvalues to show that the eigenvalues of the matrix $M$ perturbed by complex Gaussian noise have large gaps with high probability. Our results contribute to the analysis of low-rank approximations under average-case perturbations and to an understanding of eigenvalue gaps for random matrices, which may be of independent interest.

Subset Selection Based On Multiple Rankings in the Presence of Bias: Effectiveness of Fairness Constraints for Multiwinner Voting Score Functions

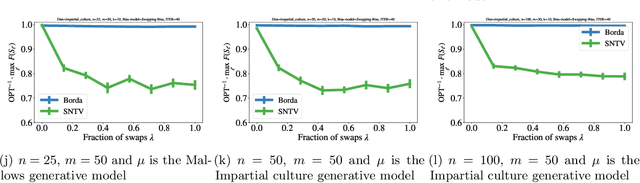
We consider the problem of subset selection where one is given multiple rankings of items and the goal is to select the highest ``quality'' subset. Score functions from the multiwinner voting literature have been used to aggregate rankings into quality scores for subsets. We study this setting of subset selection problems when, in addition, rankings may contain systemic or unconscious biases toward a group of items. For a general model of input rankings and biases, we show that requiring the selected subset to satisfy group fairness constraints can improve the quality of the selection with respect to unbiased rankings. Importantly, we show that for fairness constraints to be effective, different multiwinner score functions may require a drastically different number of rankings: While for some functions, fairness constraints need an exponential number of rankings to recover a close-to-optimal solution, for others, this dependency is only polynomial. This result relies on a novel notion of ``smoothness'' of submodular functions in this setting that quantifies how well a function can ``correctly'' assess the quality of items in the presence of bias. The results in this paper can be used to guide the choice of multiwinner score functions for the subset selection setting considered here; we additionally provide a tool to empirically enable this.

Maximizing Submodular Functions for Recommendation in the Presence of Biases

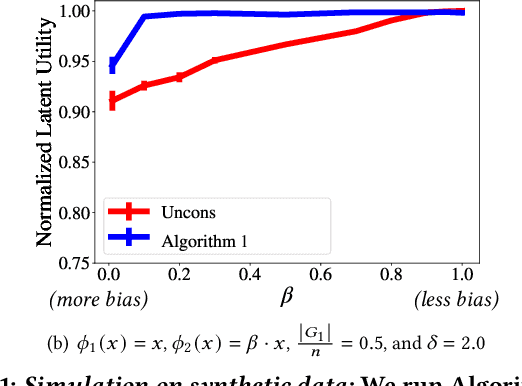
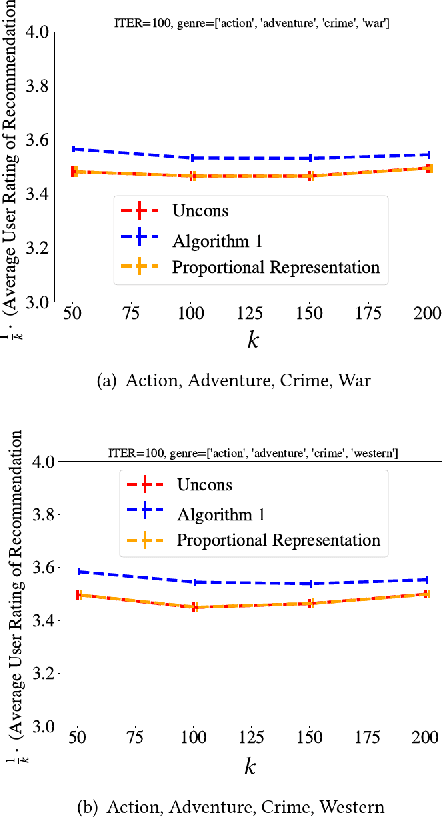
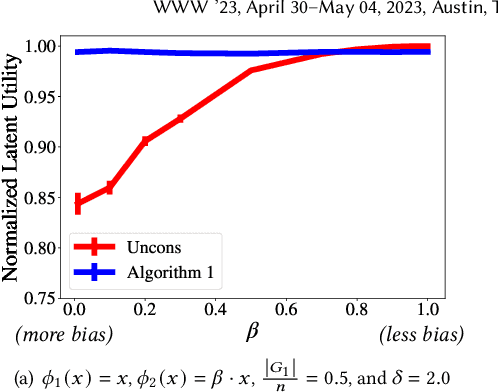
Subset selection tasks, arise in recommendation systems and search engines and ask to select a subset of items that maximize the value for the user. The values of subsets often display diminishing returns, and hence, submodular functions have been used to model them. If the inputs defining the submodular function are known, then existing algorithms can be used. In many applications, however, inputs have been observed to have social biases that reduce the utility of the output subset. Hence, interventions to improve the utility are desired. Prior works focus on maximizing linear functions -- a special case of submodular functions -- and show that fairness constraint-based interventions can not only ensure proportional representation but also achieve near-optimal utility in the presence of biases. We study the maximization of a family of submodular functions that capture functions arising in the aforementioned applications. Our first result is that, unlike linear functions, constraint-based interventions cannot guarantee any constant fraction of the optimal utility for this family of submodular functions. Our second result is an algorithm for submodular maximization. The algorithm provably outputs subsets that have near-optimal utility for this family under mild assumptions and that proportionally represent items from each group. In empirical evaluation, with both synthetic and real-world data, we observe that this algorithm improves the utility of the output subset for this family of submodular functions over baselines.

Fair Ranking with Noisy Protected Attributes

The fair-ranking problem, which asks to rank a given set of items to maximize utility subject to group fairness constraints, has received attention in the fairness, information retrieval, and machine learning literature. Recent works, however, observe that errors in socially-salient (including protected) attributes of items can significantly undermine fairness guarantees of existing fair-ranking algorithms and raise the problem of mitigating the effect of such errors. We study the fair-ranking problem under a model where socially-salient attributes of items are randomly and independently perturbed. We present a fair-ranking framework that incorporates group fairness requirements along with probabilistic information about perturbations in socially-salient attributes. We provide provable guarantees on the fairness and utility attainable by our framework and show that it is information-theoretically impossible to significantly beat these guarantees. Our framework works for multiple non-disjoint attributes and a general class of fairness constraints that includes proportional and equal representation. Empirically, we observe that, compared to baselines, our algorithm outputs rankings with higher fairness, and has a similar or better fairness-utility trade-off compared to baselines.