Picking a Representative Set of Solutions in Multiobjective Optimization: Axioms, Algorithms, and Experiments

Many real-world decision-making problems involve optimizing multiple objectives simultaneously, rendering the selection of the most preferred solution a non-trivial problem: All Pareto optimal solutions are viable candidates, and it is typically up to a decision maker to select one for implementation based on their subjective preferences. To reduce the cognitive load on the decision maker, previous work has introduced the Pareto pruning problem, where the goal is to compute a fixed-size subset of Pareto optimal solutions that best represent the full set, as evaluated by a given quality measure. Reframing Pareto pruning as a multiwinner voting problem, we conduct an axiomatic analysis of existing quality measures, uncovering several unintuitive behaviors. Motivated by these findings, we introduce a new measure, directed coverage. We also analyze the computational complexity of optimizing various quality measures, identifying previously unknown boundaries between tractable and intractable cases depending on the number and structure of the objectives. Finally, we present an experimental evaluation, demonstrating that the choice of quality measure has a decisive impact on the characteristics of the selected set of solutions and that our proposed measure performs competitively or even favorably across a range of settings.

Generative Social Choice: The Next Generation

A key task in certain democratic processes is to produce a concise slate of statements that proportionally represents the full spectrum of user opinions. This task is similar to committee elections, but unlike traditional settings, the candidate set comprises all possible statements of varying lengths, and so it can only be accessed through specific queries. Combining social choice and large language models, prior work has approached this challenge through a framework of generative social choice. We extend the framework in two fundamental ways, providing theoretical guarantees even in the face of approximately optimal queries and a budget limit on the overall length of the slate. Using GPT-4o to implement queries, we showcase our approach on datasets related to city improvement measures and drug reviews, demonstrating its effectiveness in generating representative slates from unstructured user opinions.

Drawing a Map of Elections

Our main contribution is the introduction of the map of elections framework. A map of elections consists of three main elements: (1) a dataset of elections (i.e., collections of ordinal votes over given sets of candidates), (2) a way of measuring similarities between these elections, and (3) a representation of the elections in the 2D Euclidean space as points, so that the more similar two elections are, the closer are their points. In our maps, we mostly focus on datasets of synthetic elections, but we also show an example of a map over real-life ones. To measure similarities, we would have preferred to use, e.g., the isomorphic swap distance, but this is infeasible due to its high computational complexity. Hence, we propose polynomial-time computable positionwise distance and use it instead. Regarding the representations in 2D Euclidean space, we mostly use the Kamada-Kawai algorithm, but we also show two alternatives. We develop the necessary theoretical results to form our maps and argue experimentally that they are accurate and credible. Further, we show how coloring the elections in a map according to various criteria helps in analyzing results of a number of experiments. In particular, we show colorings according to the scores of winning candidates or committees, running times of ILP-based winner determination algorithms, and approximation ratios achieved by particular algorithms.

On Sequential Fault-Intolerant Process Planning

We propose and study a planning problem we call Sequential Fault-Intolerant Process Planning (SFIPP). SFIPP captures a reward structure common in many sequential multi-stage decision problems where the planning is deemed successful only if all stages succeed. Such reward structures are different from classic additive reward structures and arise in important applications such as drug/material discovery, security, and quality-critical product design. We design provably tight online algorithms for settings in which we need to pick between different actions with unknown success chances at each stage. We do so both for the foundational case in which the behavior of actions is deterministic, and the case of probabilistic action outcomes, where we effectively balance exploration for learning and exploitation for planning through the usage of multi-armed bandit algorithms. In our empirical evaluations, we demonstrate that the specialized algorithms we develop, which leverage additional information about the structure of the SFIPP instance, outperform our more general algorithm.

Finite-Horizon Single-Pull Restless Bandits: An Efficient Index Policy For Scarce Resource Allocation

Restless multi-armed bandits (RMABs) have been highly successful in optimizing sequential resource allocation across many domains. However, in many practical settings with highly scarce resources, where each agent can only receive at most one resource, such as healthcare intervention programs, the standard RMAB framework falls short. To tackle such scenarios, we introduce Finite-Horizon Single-Pull RMABs (SPRMABs), a novel variant in which each arm can only be pulled once. This single-pull constraint introduces additional complexity, rendering many existing RMAB solutions suboptimal or ineffective. %To address this, we propose using dummy states to duplicate the system, ensuring that once an arm is activated, it transitions exclusively within the dummy states. To address this shortcoming, we propose using \textit{dummy states} that expand the system and enforce the one-pull constraint. We then design a lightweight index policy for this expanded system. For the first time, we demonstrate that our index policy achieves a sub-linearly decaying average optimality gap of $\tilde{\mathcal{O}}\left(\frac{1}{\rho^{1/2}}\right)$ for a finite number of arms, where $\rho$ is the scaling factor for each arm cluster. Extensive simulations validate the proposed method, showing robust performance across various domains compared to existing benchmarks.

Towards Foundation-model-based Multiagent System to Accelerate AI for Social Impact

AI for social impact (AI4SI) offers significant potential for addressing complex societal challenges in areas such as public health, agriculture, education, conservation, and public safety. However, existing AI4SI research is often labor-intensive and resource-demanding, limiting its accessibility and scalability; the standard approach is to design a (base-level) system tailored to a specific AI4SI problem. We propose the development of a novel meta-level multi-agent system designed to accelerate the development of such base-level systems, thereby reducing the computational cost and the burden on social impact domain experts and AI researchers. Leveraging advancements in foundation models and large language models, our proposed approach focuses on resource allocation problems providing help across the full AI4SI pipeline from problem formulation over solution design to impact evaluation. We highlight the ethical considerations and challenges inherent in deploying such systems and emphasize the importance of a human-in-the-loop approach to ensure the responsible and effective application of AI systems.

Optimizing Vital Sign Monitoring in Resource-Constrained Maternal Care: An RL-Based Restless Bandit Approach

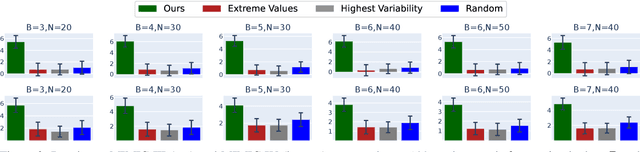
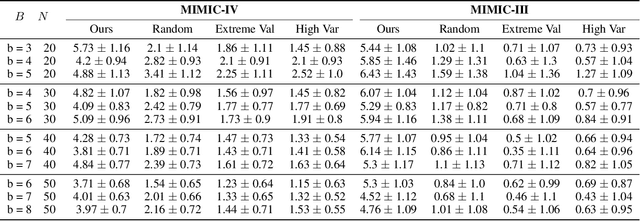
Maternal mortality remains a significant global public health challenge. One promising approach to reducing maternal deaths occurring during facility-based childbirth is through early warning systems, which require the consistent monitoring of mothers' vital signs after giving birth. Wireless vital sign monitoring devices offer a labor-efficient solution for continuous monitoring, but their scarcity raises the critical question of how to allocate them most effectively. We devise an allocation algorithm for this problem by modeling it as a variant of the popular Restless Multi-Armed Bandit (RMAB) paradigm. In doing so, we identify and address novel, previously unstudied constraints unique to this domain, which render previous approaches for RMABs unsuitable and significantly increase the complexity of the learning and planning problem. To overcome these challenges, we adopt the popular Proximal Policy Optimization (PPO) algorithm from reinforcement learning to learn an allocation policy by training a policy and value function network. We demonstrate in simulations that our approach outperforms the best heuristic baseline by up to a factor of $4$.

Balancing Act: Prioritization Strategies for LLM-Designed Restless Bandit Rewards

LLMs are increasingly used to design reward functions based on human preferences in Reinforcement Learning (RL). We focus on LLM-designed rewards for Restless Multi-Armed Bandits, a framework for allocating limited resources among agents. In applications such as public health, this approach empowers grassroots health workers to tailor automated allocation decisions to community needs. In the presence of multiple agents, altering the reward function based on human preferences can impact subpopulations very differently, leading to complex tradeoffs and a multi-objective resource allocation problem. We are the first to present a principled method termed Social Choice Language Model for dealing with these tradeoffs for LLM-designed rewards for multiagent planners in general and restless bandits in particular. The novel part of our model is a transparent and configurable selection component, called an adjudicator, external to the LLM that controls complex tradeoffs via a user-selected social welfare function. Our experiments demonstrate that our model reliably selects more effective, aligned, and balanced reward functions compared to purely LLM-based approaches.

Multiwinner Temporal Voting with Aversion to Change

We study two-stage committee elections where voters have dynamic preferences over candidates; at each stage, a committee is chosen under a given voting rule. We are interested in identifying a winning committee for the second stage that overlaps as much as possible with the first-stage committee. We show a full complexity dichotomy for the class of Thiele rules: this problem is tractable for Approval Voting (AV) and hard for all other Thiele rules (including, in particular, Proportional Approval Voting and the Chamberlin-Courant rule). We extend this dichotomy to the greedy variants of Thiele rules. We also explore this problem from a parameterized complexity perspective for several natural parameters. We complement the theory with experimental analysis: e.g., we investigate the average number of changes in the committee as a function of changes in voters' preferences and the role of ties.

Evaluating the Effectiveness of Index-Based Treatment Allocation

When resources are scarce, an allocation policy is needed to decide who receives a resource. This problem occurs, for instance, when allocating scarce medical resources and is often solved using modern ML methods. This paper introduces methods to evaluate index-based allocation policies -- that allocate a fixed number of resources to those who need them the most -- by using data from a randomized control trial. Such policies create dependencies between agents, which render the assumptions behind standard statistical tests invalid and limit the effectiveness of estimators. Addressing these challenges, we translate and extend recent ideas from the statistics literature to present an efficient estimator and methods for computing asymptotically correct confidence intervals. This enables us to effectively draw valid statistical conclusions, a critical gap in previous work. Our extensive experiments validate our methodology in practical settings, while also showcasing its statistical power. We conclude by proposing and empirically verifying extensions of our methodology that enable us to reevaluate a past randomized control trial to evaluate different ML allocation policies in the context of a mHealth program, drawing previously invisible conclusions.