Drawing a Map of Elections

Our main contribution is the introduction of the map of elections framework. A map of elections consists of three main elements: (1) a dataset of elections (i.e., collections of ordinal votes over given sets of candidates), (2) a way of measuring similarities between these elections, and (3) a representation of the elections in the 2D Euclidean space as points, so that the more similar two elections are, the closer are their points. In our maps, we mostly focus on datasets of synthetic elections, but we also show an example of a map over real-life ones. To measure similarities, we would have preferred to use, e.g., the isomorphic swap distance, but this is infeasible due to its high computational complexity. Hence, we propose polynomial-time computable positionwise distance and use it instead. Regarding the representations in 2D Euclidean space, we mostly use the Kamada-Kawai algorithm, but we also show two alternatives. We develop the necessary theoretical results to form our maps and argue experimentally that they are accurate and credible. Further, we show how coloring the elections in a map according to various criteria helps in analyzing results of a number of experiments. In particular, we show colorings according to the scores of winning candidates or committees, running times of ILP-based winner determination algorithms, and approximation ratios achieved by particular algorithms.

Achieving Fully Proportional Representation: Approximability Results

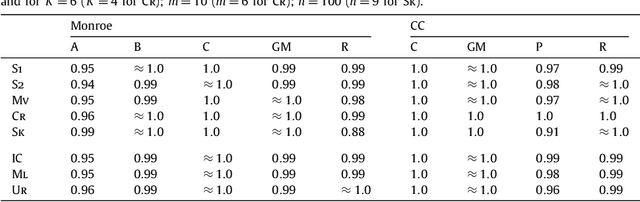
We study the complexity of (approximate) winner determination under the Monroe and Chamberlin--Courant multiwinner voting rules, which determine the set of representatives by optimizing the total (dis)satisfaction of the voters with their representatives. The total (dis)satisfaction is calculated either as the sum of individual (dis)satisfactions (the utilitarian case) or as the (dis)satisfaction of the worst off voter (the egalitarian case). We provide good approximation algorithms for the satisfaction-based utilitarian versions of the Monroe and Chamberlin--Courant rules, and inapproximability results for the dissatisfaction-based utilitarian versions of them and also for all egalitarian cases. Our algorithms are applicable and particularly appealing when voters submit truncated ballots. We provide experimental evaluation of the algorithms both on real-life preference-aggregation data and on synthetic data. These experiments show that our simple and fast algorithms can in many cases find near-perfect solutions.