Drawing a Map of Elections

Our main contribution is the introduction of the map of elections framework. A map of elections consists of three main elements: (1) a dataset of elections (i.e., collections of ordinal votes over given sets of candidates), (2) a way of measuring similarities between these elections, and (3) a representation of the elections in the 2D Euclidean space as points, so that the more similar two elections are, the closer are their points. In our maps, we mostly focus on datasets of synthetic elections, but we also show an example of a map over real-life ones. To measure similarities, we would have preferred to use, e.g., the isomorphic swap distance, but this is infeasible due to its high computational complexity. Hence, we propose polynomial-time computable positionwise distance and use it instead. Regarding the representations in 2D Euclidean space, we mostly use the Kamada-Kawai algorithm, but we also show two alternatives. We develop the necessary theoretical results to form our maps and argue experimentally that they are accurate and credible. Further, we show how coloring the elections in a map according to various criteria helps in analyzing results of a number of experiments. In particular, we show colorings according to the scores of winning candidates or committees, running times of ILP-based winner determination algorithms, and approximation ratios achieved by particular algorithms.

Proportionality in Thumbs Up and Down Voting

Consider the decision-making setting where agents elect a panel by expressing both positive and negative preferences. Prominently, in constitutional AI, citizens democratically select a slate of ethical preferences on which a foundation model is to be trained. There, in practice, agents may both approve and disapprove of different ethical principles. Proportionality has been well-studied in computational social choice for approval ballots, but its meaning remains unclear when negative sentiments are also considered. In this work, we propose two conceptually distinct approaches to interpret proportionality in the presence of up and down votes. The first approach treats the satisfaction from electing candidates and the impact of vetoing them as comparable, leading to combined proportionality guarantees. The second approach considers veto power separately, introducing guarantees distinct from traditional proportionality. We formalize axioms for each perspective and examine their satisfiability by suitable adaptations of Phragm\'en's rule, Proportional Approval Voting rule and the Method of Equal Shares.

Proportional Selection in Networks

We address the problem of selecting $k$ representative nodes from a network, aiming to achieve two objectives: identifying the most influential nodes and ensuring the selection proportionally reflects the network's diversity. We propose two approaches to accomplish this, analyze them theoretically, and demonstrate their effectiveness through a series of experiments.

Online Approval Committee Elections

Assume $k$ candidates need to be selected. The candidates appear over time. Each time one appears, it must be immediately selected or rejected -- a decision that is made by a group of individuals through voting. Assume the voters use approval ballots, i.e., for each candidate they only specify whether they consider it acceptable or not. This setting can be seen as a voting variant of choosing $k$ secretaries. Our contribution is twofold. (1) We assess to what extent the committees that are computed online can proportionally represent the voters. (2) If a prior probability over candidate approvals is available, we show how to compute committees with maximal expected score.

Core-Stable Committees under Restricted Domains

We study the setting of committee elections, where a group of individuals needs to collectively select a given size subset of available objects. This model is relevant for a number of real-life scenarios including political elections, participatory budgeting, and facility-location. We focus on the core -- the classic notion of proportionality, stability and fairness. We show that for a number of restricted domains including voter-interval, candidate-interval, single-peaked, and single-crossing preferences the core is non-empty and can be found in polynomial time. We show that the core might be empty for strict top-monotonic preferences, yet we introduce a relaxation of this class, which guarantees non-emptiness of the core. Our algorithms work both in the randomized and discrete models. We also show that the classic known proportional rules do not return committees from the core even for the most restrictive domains among those we consider (in particular for 1D-Euclidean preferences). We additionally prove a number of structural results that give better insights into the nature of some of the restricted domains, and which in particular give a better intuitive understanding of the class of top-monotonic preferences.

Bribery as a Measure of Candidate Success: Complexity Results for Approval-Based Multiwinner Rules

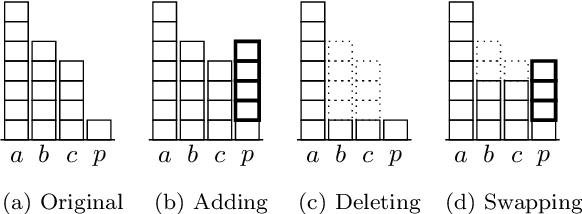
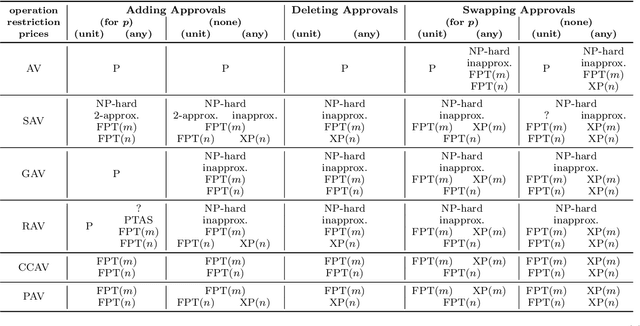
We study the problem of bribery in multiwinner elections, for the case where the voters cast approval ballots (i.e., sets of candidates they approve) and the bribery actions are limited to: adding an approval to a vote, deleting an approval from a vote, or moving an approval within a vote from one candidate to the other. We consider a number of approval-based multiwinner rules (AV, SAV, GAV, RAV, approval-based Chamberlin--Courant, and PAV). We find the landscape of complexity results quite rich, going from polynomial-time algorithms through NP-hardness with constant-factor approximations, to outright inapproximability. Moreover, in general, our problems tend to be easier when we limit out bribery actions on increasing the number of approvals of the candidate that we want to be in a winning committee (i.e., adding approvals only for this preferred candidate, or moving approvals only to him or her). We also study parameterized complexity of our problems, with a focus on parameterizations by the numbers of voters or candidates.

A Quantitative Analysis of Multi-Winner Rules

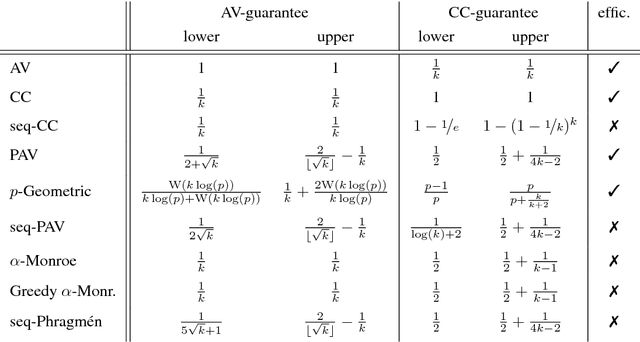
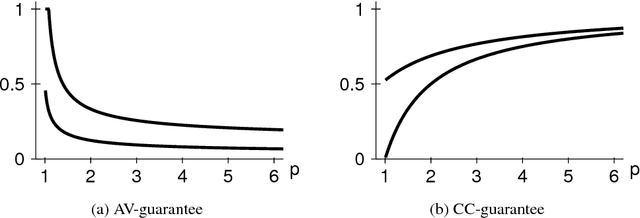
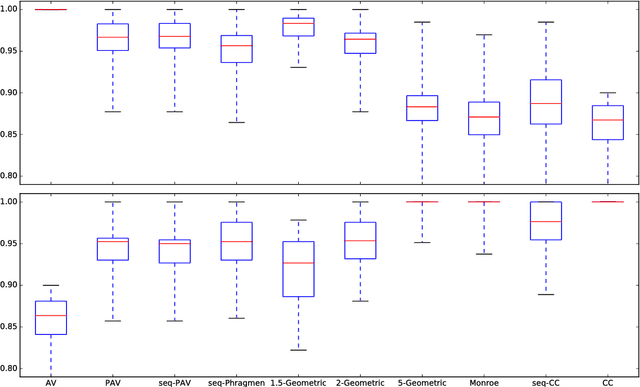
To choose a suitable multi-winner rule, i.e., a voting rule for selecting a subset of $k$ alternatives based on a collection of preferences, is a hard and ambiguous task. Depending on the context, it varies widely what constitutes the choice of an "optimal" subset. In this paper, we offer a new perspective to measure the quality of such subsets and---consequently---multi-winner rules. We provide a quantitative analysis using methods from the theory of approximation algorithms and estimate how well multi-winner rules approximate two extreme objectives: diversity as captured by the (Approval) Chamberlin--Courant rule and individual excellence as captured by Multi-winner Approval Voting. With both theoretical and experimental methods we classify multi-winner rules in terms of their quantitative alignment with these two opposing objectives.

Proportional Rankings

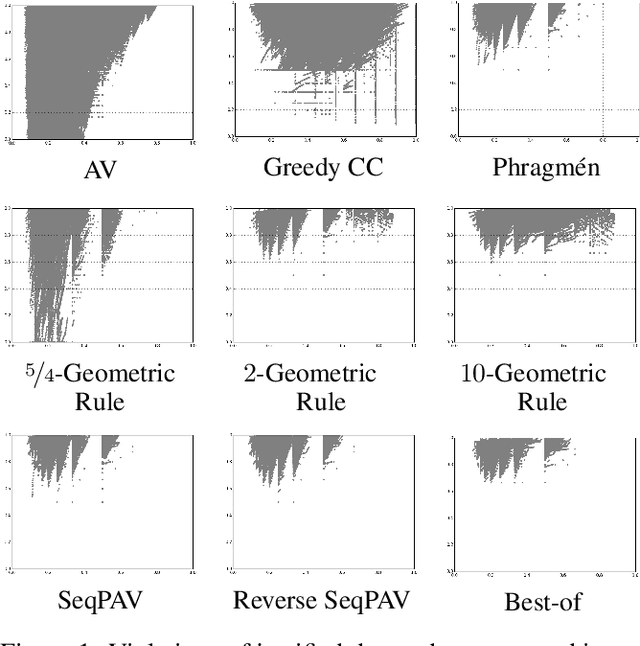
In this paper we extend the principle of proportional representation to rankings. We consider the setting where alternatives need to be ranked based on approval preferences. In this setting, proportional representation requires that cohesive groups of voters are represented proportionally in each initial segment of the ranking. Proportional rankings are desirable in situations where initial segments of different lengths may be relevant, e.g., hiring decisions (if it is unclear how many positions are to be filled), the presentation of competing proposals on a liquid democracy platform (if it is unclear how many proposals participants are taking into consideration), or recommender systems (if a ranking has to accommodate different user types). We study the proportional representation provided by several ranking methods and prove theoretical guarantees. Furthermore, we experimentally evaluate these methods and present preliminary evidence as to which methods are most suitable for producing proportional rankings.

Multiwinner Approval Rules as Apportionment Methods

We establish a link between multiwinner elections and apportionment problems by showing how approval-based multiwinner election rules can be interpreted as methods of apportionment. We consider several multiwinner rules and observe that they induce apportionment methods that are well-established in the literature on proportional representation. For instance, we show that Proportional Approval Voting induces the D'Hondt method and that Monroe's rule induces the largest reminder method. We also consider properties of apportionment methods and exhibit multiwinner rules that induce apportionment methods satisfying these properties.

Finding a Collective Set of Items: From Proportional Multirepresentation to Group Recommendation

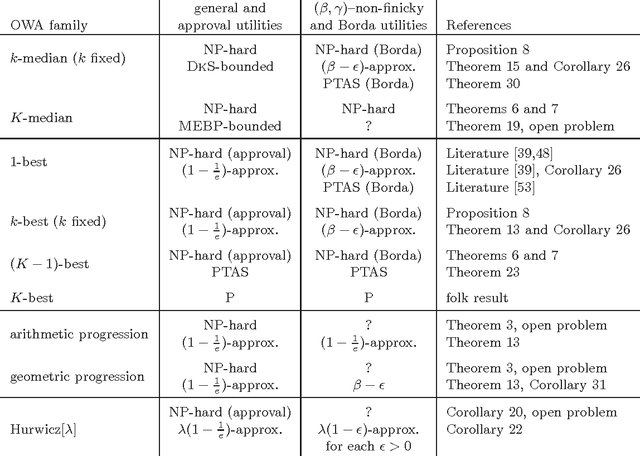
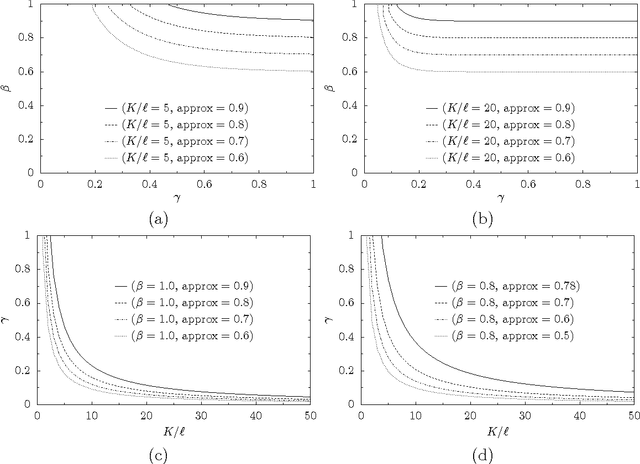
We consider the following problem: There is a set of items (e.g., movies) and a group of agents (e.g., passengers on a plane); each agent has some intrinsic utility for each of the items. Our goal is to pick a set of $K$ items that maximize the total derived utility of all the agents (i.e., in our example we are to pick $K$ movies that we put on the plane's entertainment system). However, the actual utility that an agent derives from a given item is only a fraction of its intrinsic one, and this fraction depends on how the agent ranks the item among the chosen, available, ones. We provide a formal specification of the model and provide concrete examples and settings where it is applicable. We show that the problem is hard in general, but we show a number of tractability results for its natural special cases.