Finding a Collective Set of Items: From Proportional Multirepresentation to Group Recommendation
Paper and Code
Jan 08, 2016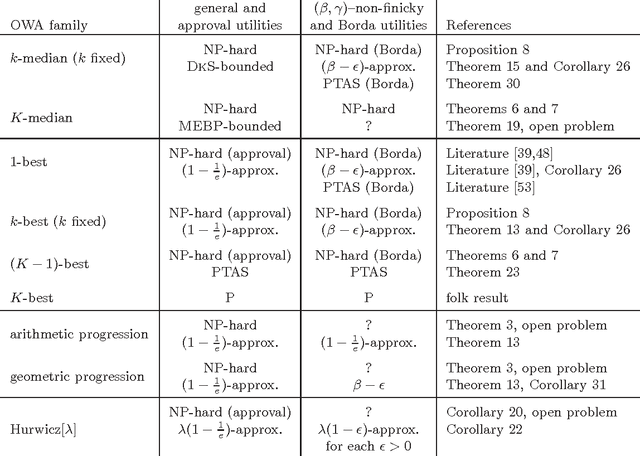
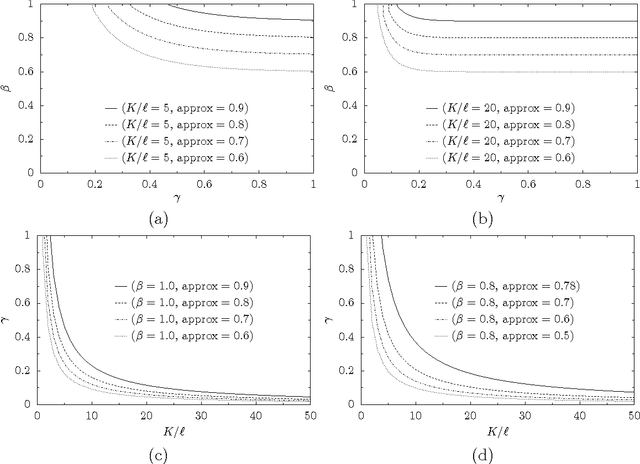
We consider the following problem: There is a set of items (e.g., movies) and a group of agents (e.g., passengers on a plane); each agent has some intrinsic utility for each of the items. Our goal is to pick a set of $K$ items that maximize the total derived utility of all the agents (i.e., in our example we are to pick $K$ movies that we put on the plane's entertainment system). However, the actual utility that an agent derives from a given item is only a fraction of its intrinsic one, and this fraction depends on how the agent ranks the item among the chosen, available, ones. We provide a formal specification of the model and provide concrete examples and settings where it is applicable. We show that the problem is hard in general, but we show a number of tractability results for its natural special cases.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge