Piotr Faliszewski
Diversity of Structured Domains via k-Kemeny Scores
Sep 19, 2025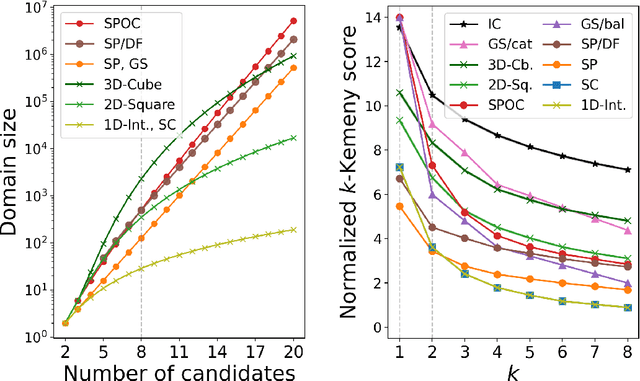
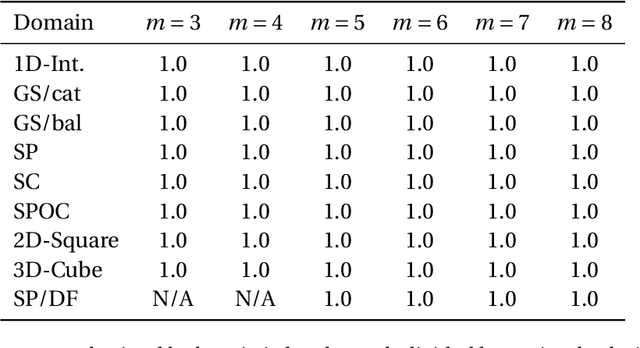
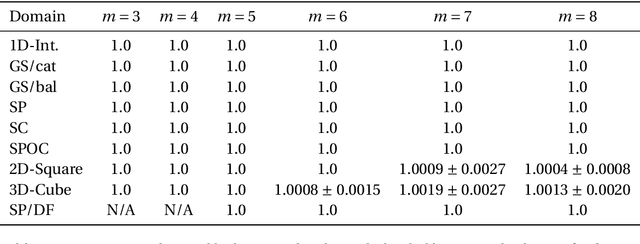
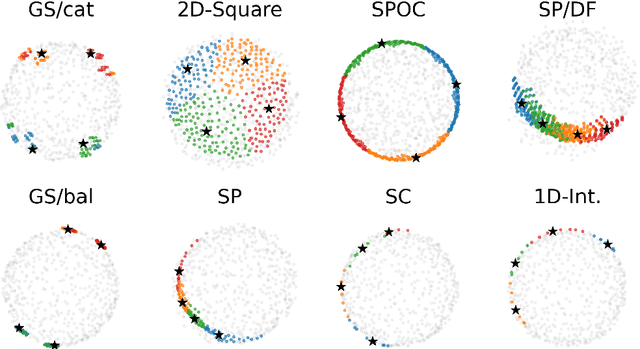
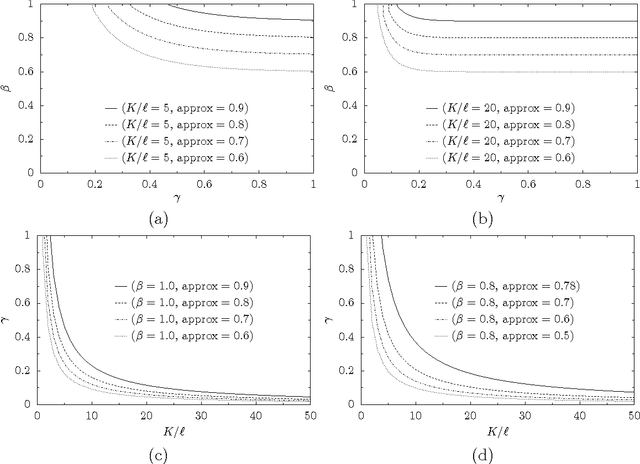
Abstract:In the k-Kemeny problem, we are given an ordinal election, i.e., a collection of votes ranking the candidates from best to worst, and we seek the smallest number of swaps of adjacent candidates that ensure that the election has at most k different rankings. We study this problem for a number of structured domains, including the single-peaked, single-crossing, group-separable, and Euclidean ones. We obtain two kinds of results: (1) We show that k-Kemeny remains intractable under most of these domains, even for k=2, and (2) we use k-Kemeny to rank these domains in terms of their diversity.
Drawing a Map of Elections
Apr 08, 2025Abstract:Our main contribution is the introduction of the map of elections framework. A map of elections consists of three main elements: (1) a dataset of elections (i.e., collections of ordinal votes over given sets of candidates), (2) a way of measuring similarities between these elections, and (3) a representation of the elections in the 2D Euclidean space as points, so that the more similar two elections are, the closer are their points. In our maps, we mostly focus on datasets of synthetic elections, but we also show an example of a map over real-life ones. To measure similarities, we would have preferred to use, e.g., the isomorphic swap distance, but this is infeasible due to its high computational complexity. Hence, we propose polynomial-time computable positionwise distance and use it instead. Regarding the representations in 2D Euclidean space, we mostly use the Kamada-Kawai algorithm, but we also show two alternatives. We develop the necessary theoretical results to form our maps and argue experimentally that they are accurate and credible. Further, we show how coloring the elections in a map according to various criteria helps in analyzing results of a number of experiments. In particular, we show colorings according to the scores of winning candidates or committees, running times of ILP-based winner determination algorithms, and approximation ratios achieved by particular algorithms.
Expected Frequency Matrices of Elections: Computation, Geometry, and Preference Learning
May 16, 2022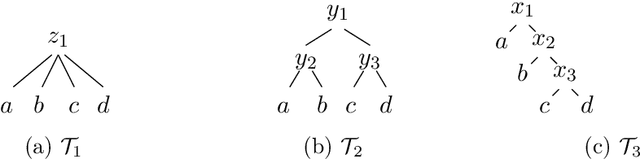

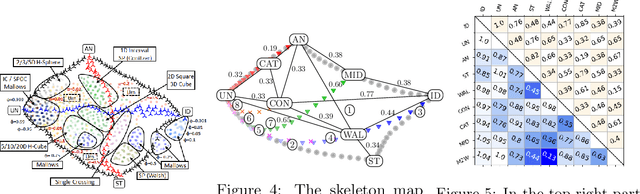
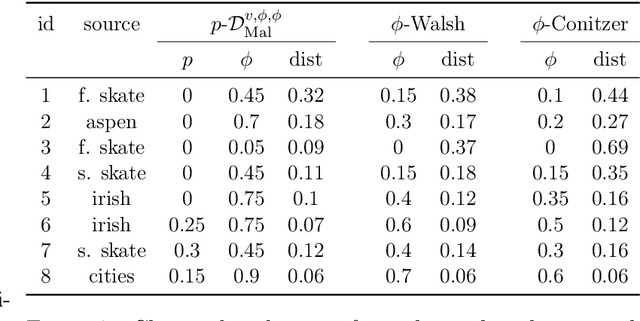
Abstract:We use the "map of elections" approach of Szufa et al. (AAMAS 2020) to analyze several well-known vote distributions. For each of them, we give an explicit formula or an efficient algorithm for computing its frequency matrix, which captures the probability that a given candidate appears in a given position in a sampled vote. We use these matrices to draw the "skeleton map" of distributions, evaluate its robustness, and analyze its properties. We further use them to identify the nature of several real-world elections.
Bribery as a Measure of Candidate Success: Complexity Results for Approval-Based Multiwinner Rules
Apr 19, 2021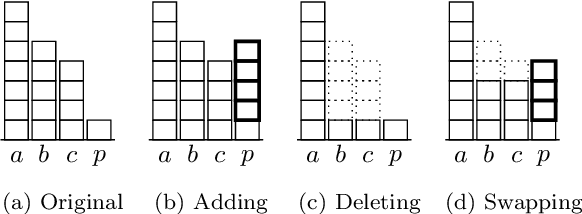
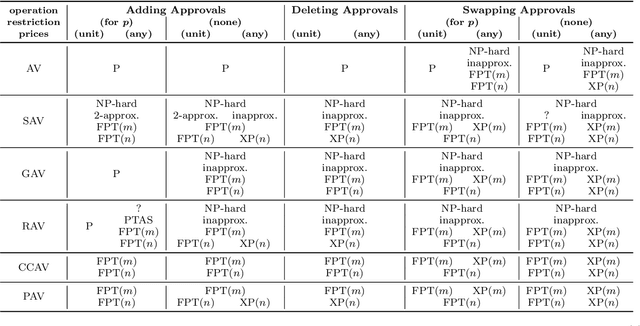
Abstract:We study the problem of bribery in multiwinner elections, for the case where the voters cast approval ballots (i.e., sets of candidates they approve) and the bribery actions are limited to: adding an approval to a vote, deleting an approval from a vote, or moving an approval within a vote from one candidate to the other. We consider a number of approval-based multiwinner rules (AV, SAV, GAV, RAV, approval-based Chamberlin--Courant, and PAV). We find the landscape of complexity results quite rich, going from polynomial-time algorithms through NP-hardness with constant-factor approximations, to outright inapproximability. Moreover, in general, our problems tend to be easier when we limit out bribery actions on increasing the number of approvals of the candidate that we want to be in a winning committee (i.e., adding approvals only for this preferred candidate, or moving approvals only to him or her). We also study parameterized complexity of our problems, with a focus on parameterizations by the numbers of voters or candidates.
Algorithms for Destructive Shift Bribery
Oct 03, 2018
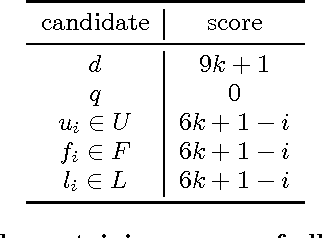
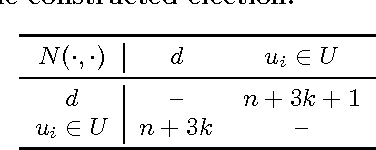
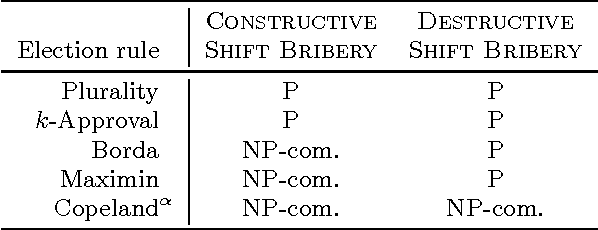
Abstract:We study the complexity of Destructive Shift Bribery. In this problem, we are given an election with a set of candidates and a set of voters (each ranking the candidates from the best to the worst), a despised candidate $d$, a budget $B$, and prices for shifting $d$ back in the voters' rankings. The goal is to ensure that $d$ is not a winner of the election. We show that this problem is polynomial-time solvable for scoring protocols (encoded in unary), the Bucklin and Simplified Bucklin rules, and the Maximin rule, but is NP-hard for the Copeland rule. This stands in contrast to the results for the constructive setting (known from the literature), for which the problem is polynomial-time solvable for $k$-Approval family of rules, but is NP-hard for the Borda, Copeland, and Maximin rules. We complement the analysis of the Copeland rule showing W-hardness for the parameterization by the budget value, and by the number of affected voters. We prove that the problem is W-hard when parameterized by the number of voters even for unit prices. From the positive perspective we provide an efficient algorithm for solving the problem parameterized by the combined parameter the number of candidates and the maximum bribery price (alternatively the number of different bribery prices).
Complexity of Shift Bribery in Committee Elections
Sep 24, 2018
Abstract:Given an election, a preferred candidate p, and a budget, the SHIFT BRIBERY problem asks whether p can win the election after shifting p higher in some voters' preference orders. Of course, shifting comes at a price (depending on the voter and on the extent of the shift) and one must not exceed the given budget. We study the (parameterized) computational complexity of S HIFT BRIBERY for multiwinner voting rules where winning the election means to be part of some winning committee. We focus on the well-established SNTV, Bloc, k-Borda, and Chamberlin-Courant rules, as well as on approximate variants of the Chamberlin-Courant rule, since the original rule is NP-hard to compute. We show that SHIFT BRIBERY tends to be harder in the multiwinner setting than in the single-winner one by showing settings where SHIFT BRIBERY is easy in the single-winner cases, but is hard (and hard to approximate) in the multiwinner ones. Moreover, we show that the non-monotonicity of those rules which are based on approximation algorithms for the Chamberlin-Courant rule sometimes affects the complexity of SHIFT BRIBERY.
A Framework for Approval-based Budgeting Methods
Sep 12, 2018
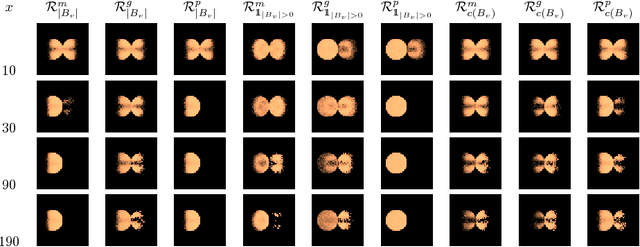

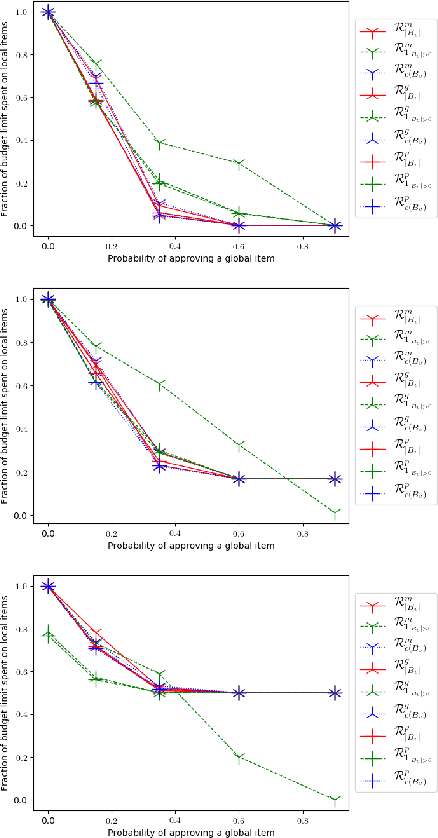
Abstract:We define and study a general framework for approval-based budgeting methods and compare certain methods within this framework by their axiomatic and computational properties. Furthermore, we visualize their behavior on certain Euclidean distributions and analyze them experimentally.
Elections with Few Voters: Candidate Control Can Be Easy
Mar 18, 2017
Abstract:We study the computational complexity of candidate control in elections with few voters, that is, we consider the parameterized complexity of candidate control in elections with respect to the number of voters as a parameter. We consider both the standard scenario of adding and deleting candidates, where one asks whether a given candidate can become a winner (or, in the destructive case, can be precluded from winning) by adding or deleting few candidates, as well as a combinatorial scenario where adding/deleting a candidate automatically means adding or deleting a whole group of candidates. Considering several fundamental voting rules, our results show that the parameterized complexity of candidate control, with the number of voters as the parameter, is much more varied than in the setting with many voters.
Finding a Collective Set of Items: From Proportional Multirepresentation to Group Recommendation
Jan 08, 2016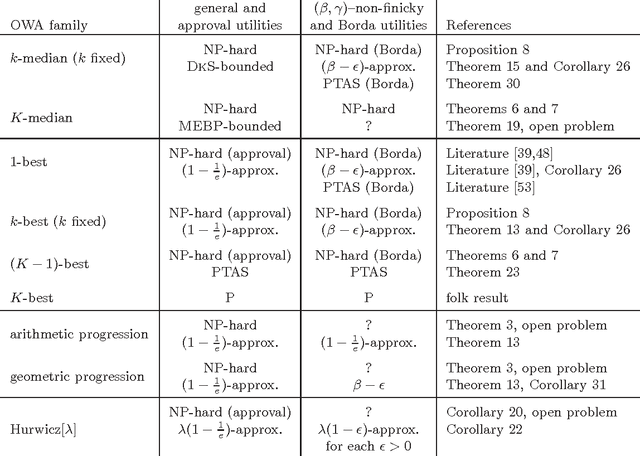
Abstract:We consider the following problem: There is a set of items (e.g., movies) and a group of agents (e.g., passengers on a plane); each agent has some intrinsic utility for each of the items. Our goal is to pick a set of $K$ items that maximize the total derived utility of all the agents (i.e., in our example we are to pick $K$ movies that we put on the plane's entertainment system). However, the actual utility that an agent derives from a given item is only a fraction of its intrinsic one, and this fraction depends on how the agent ranks the item among the chosen, available, ones. We provide a formal specification of the model and provide concrete examples and settings where it is applicable. We show that the problem is hard in general, but we show a number of tractability results for its natural special cases.
Achieving Fully Proportional Representation: Approximability Results
Dec 14, 2013


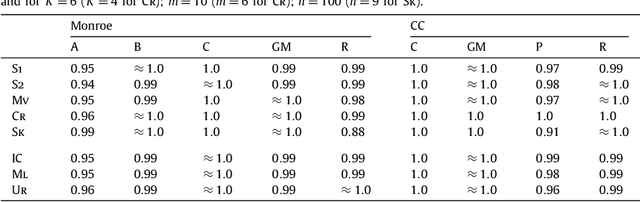
Abstract:We study the complexity of (approximate) winner determination under the Monroe and Chamberlin--Courant multiwinner voting rules, which determine the set of representatives by optimizing the total (dis)satisfaction of the voters with their representatives. The total (dis)satisfaction is calculated either as the sum of individual (dis)satisfactions (the utilitarian case) or as the (dis)satisfaction of the worst off voter (the egalitarian case). We provide good approximation algorithms for the satisfaction-based utilitarian versions of the Monroe and Chamberlin--Courant rules, and inapproximability results for the dissatisfaction-based utilitarian versions of them and also for all egalitarian cases. Our algorithms are applicable and particularly appealing when voters submit truncated ballots. We provide experimental evaluation of the algorithms both on real-life preference-aggregation data and on synthetic data. These experiments show that our simple and fast algorithms can in many cases find near-perfect solutions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge