Verifying Proportionality in Temporal Voting

We study a model of temporal voting where there is a fixed time horizon, and at each round the voters report their preferences over the available candidates and a single candidate is selected. Prior work has adapted popular notions of justified representation as well as voting rules that provide strong representation guarantees from the multiwinner election setting to this model. In our work, we focus on the complexity of verifying whether a given outcome offers proportional representation. We show that in the temporal setting verification is strictly harder than in multiwinner voting, but identify natural special cases that enable efficient algorithms.

Temporal Fair Division of Indivisible Items

We study a fair division model where indivisible items arrive sequentially, and must be allocated immediately and irrevocably. Previous work on online fair division has shown impossibility results in achieving approximate envy-freeness under these constraints. In contrast, we consider an informed setting where the algorithm has complete knowledge of future items, and aim to ensure that the cumulative allocation at each round satisfies approximate envy-freeness -- which we define as temporal envy-freeness up to one item (TEF1). We focus on settings where items can be exclusively goods or exclusively chores. For goods, while TEF1 allocations may not always exist, we identify several special cases where they do -- two agents, two item types, generalized binary valuations, unimodal preferences -- and provide polynomial-time algorithms for these cases. We also prove that determining the existence of a TEF1 allocation is NP-hard. For chores, we establish analogous results for the special cases, but present a slightly weaker intractability result. We also establish the incompatibility between TEF1 and Pareto-optimality, with the implication that it is intractable to find a TEF1 allocation that maximizes any $p$-mean welfare, even for two agents.

Temporal Elections: Welfare, Strategyproofness, and Proportionality

We investigate a model of sequential decision-making where a single alternative is chosen at each round. We focus on two objectives-utilitarian welfare (Util) and egalitarian welfare (Egal)-and consider the computational complexity of the associated maximization problems, as well as their compatibility with strategyproofness and proportionality. We observe that maximizing Util is easy, but the corresponding decision problem for Egal is NP-complete even in restricted cases. We complement this hardness result for Egal with parameterized complexity analysis and an approximation algorithm. Additionally, we show that, while a mechanism that outputs a Util outcome is strategyproof, all deterministic mechanisms for computing Egal outcomes fail a very weak variant of strategyproofness, called non-obvious manipulability (NOM). However, we show that when agents have non-empty approval sets at each timestep, choosing an Egal-maximizing outcome while breaking ties lexicographically satisfies NOM. Regarding proportionality, we prove that a proportional (PROP) outcome can be computed efficiently, but finding an outcome that maximizes Util while guaranteeing PROP is NP-hard. We also derive upper and lower bounds on the price of proportionality with respect to Util and Egal.

Multiwinner Temporal Voting with Aversion to Change

We study two-stage committee elections where voters have dynamic preferences over candidates; at each stage, a committee is chosen under a given voting rule. We are interested in identifying a winning committee for the second stage that overlaps as much as possible with the first-stage committee. We show a full complexity dichotomy for the class of Thiele rules: this problem is tractable for Approval Voting (AV) and hard for all other Thiele rules (including, in particular, Proportional Approval Voting and the Chamberlin-Courant rule). We extend this dichotomy to the greedy variants of Thiele rules. We also explore this problem from a parameterized complexity perspective for several natural parameters. We complement the theory with experimental analysis: e.g., we investigate the average number of changes in the committee as a function of changes in voters' preferences and the role of ties.

Select to Perfect: Imitating desired behavior from large multi-agent data

AI agents are commonly trained with large datasets of demonstrations of human behavior. However, not all behaviors are equally safe or desirable. Desired characteristics for an AI agent can be expressed by assigning desirability scores, which we assume are not assigned to individual behaviors but to collective trajectories. For example, in a dataset of vehicle interactions, these scores might relate to the number of incidents that occurred. We first assess the effect of each individual agent's behavior on the collective desirability score, e.g., assessing how likely an agent is to cause incidents. This allows us to selectively imitate agents with a positive effect, e.g., only imitating agents that are unlikely to cause incidents. To enable this, we propose the concept of an agent's Exchange Value, which quantifies an individual agent's contribution to the collective desirability score. The Exchange Value is the expected change in desirability score when substituting the agent for a randomly selected agent. We propose additional methods for estimating Exchange Values from real-world datasets, enabling us to learn desired imitation policies that outperform relevant baselines. The project website can be found at https://tinyurl.com/select-to-perfect.

Temporal Fairness in Multiwinner Voting

Multiwinner voting captures a wide variety of settings, from parliamentary elections in democratic systems to product placement in online shopping platforms. There is a large body of work dealing with axiomatic characterizations, computational complexity, and algorithmic analysis of multiwinner voting rules. Although many challenges remain, significant progress has been made in showing existence of fair and representative outcomes as well as efficient algorithmic solutions for many commonly studied settings. However, much of this work focuses on single-shot elections, even though in numerous real-world settings elections are held periodically and repeatedly. Hence, it is imperative to extend the study of multiwinner voting to temporal settings. Recently, there have been several efforts to address this challenge. However, these works are difficult to compare, as they model multi-period voting in very different ways. We propose a unified framework for studying temporal fairness in this domain, drawing connections with various existing bodies of work, and consolidating them within a general framework. We also identify gaps in existing literature, outline multiple opportunities for future work, and put forward a vision for the future of multiwinner voting in temporal settings.

Expected Frequency Matrices of Elections: Computation, Geometry, and Preference Learning

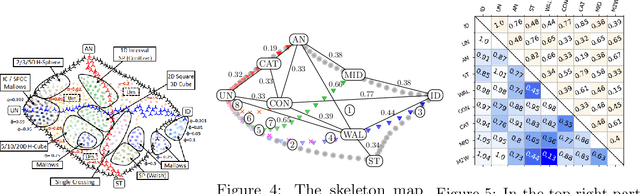
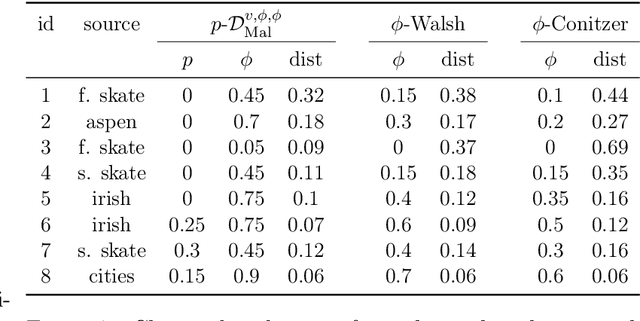
We use the "map of elections" approach of Szufa et al. (AAMAS 2020) to analyze several well-known vote distributions. For each of them, we give an explicit formula or an efficient algorithm for computing its frequency matrix, which captures the probability that a given candidate appears in a given position in a sampled vote. We use these matrices to draw the "skeleton map" of distributions, evaluate its robustness, and analyze its properties. We further use them to identify the nature of several real-world elections.

Proportional Rankings

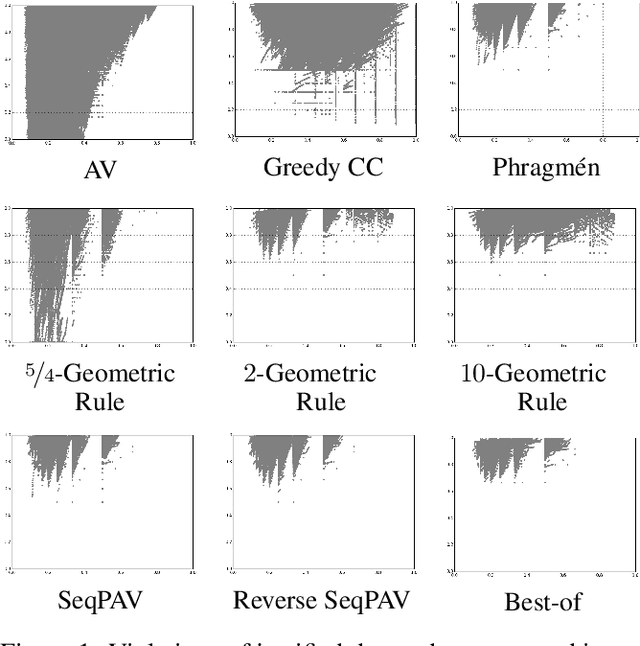
In this paper we extend the principle of proportional representation to rankings. We consider the setting where alternatives need to be ranked based on approval preferences. In this setting, proportional representation requires that cohesive groups of voters are represented proportionally in each initial segment of the ranking. Proportional rankings are desirable in situations where initial segments of different lengths may be relevant, e.g., hiring decisions (if it is unclear how many positions are to be filled), the presentation of competing proposals on a liquid democracy platform (if it is unclear how many proposals participants are taking into consideration), or recommender systems (if a ranking has to accommodate different user types). We study the proportional representation provided by several ranking methods and prove theoretical guarantees. Furthermore, we experimentally evaluate these methods and present preliminary evidence as to which methods are most suitable for producing proportional rankings.

The Cost of Stability in Coalitional Games

A key question in cooperative game theory is that of coalitional stability, usually captured by the notion of the \emph{core}--the set of outcomes such that no subgroup of players has an incentive to deviate. However, some coalitional games have empty cores, and any outcome in such a game is unstable. In this paper, we investigate the possibility of stabilizing a coalitional game by using external payments. We consider a scenario where an external party, which is interested in having the players work together, offers a supplemental payment to the grand coalition (or, more generally, a particular coalition structure). This payment is conditional on players not deviating from their coalition(s). The sum of this payment plus the actual gains of the coalition(s) may then be divided among the agents so as to promote stability. We define the \emph{cost of stability (CoS)} as the minimal external payment that stabilizes the game. We provide general bounds on the cost of stability in several classes of games, and explore its algorithmic properties. To develop a better intuition for the concepts we introduce, we provide a detailed algorithmic study of the cost of stability in weighted voting games, a simple but expressive class of games which can model decision-making in political bodies, and cooperation in multiagent settings. Finally, we extend our model and results to games with coalition structures.