Efficient Ensemble Selection from Binary and Pairwise Feedback

Organizations increasingly deploy multiple AI systems across task domains, but selecting a small, high-performing ensemble can require costly model calls, benchmark runs, and human evaluation. We study this selection problem as a distributional variant of multiwinner voting: tasks are drawn from an unknown domain distribution, each task induces feedback over candidate experts, and a committee's value on a task is determined by its best-performing member. We analyze both binary feedback, for tasks with correct/incorrect outcomes, and pairwise feedback, for tasks where candidate outputs are compared by preference. In the binary setting, the induced objective is coverage. We give exhaustive-elicitation baselines and matching worst-case query lower bounds, and we design a failure-conditioned greedy algorithm that preserves the standard $(1-1/e)$ guarantee while obtaining instance-dependent query savings. In the pairwise setting, we study $θ$-winning committees. We show that full-information optimization admits a PTAS but no EPTAS under Gap-ETH, and that the objective is monotone but not submodular. This motivates a weighted ordinal coverage relaxation, which is submodular and supports a failure-conditioned greedy oracle under pairwise feedback. We then convert this oracle back into $θ$-type guarantees through finite-family auditing or a minimax wrapper. We also provide small-scale LLM experiments illustrating the predicted query savings and the role of complementarity in committee selection.

Learning Unanimously Acceptable Lotteries via Queries

Many high-stakes AI deployments proceed only if every stakeholder deems the system acceptable relative to their own minimum standard. With randomization over a finite menu of options, this becomes a feasibility question: does there exist a lottery over options that clears all stakeholders' acceptability bars? We study a query model where the algorithm proposes lotteries and receives only binary accept/reject feedback. We give deterministic and randomized algorithms that either find a unanimously acceptable lottery or certify infeasibility; adaptivity can avoid eliciting many stakeholders' constraints, and randomization further reduces the expected elicitation cost relative to full elicitation. We complement these upper bounds with worst-case lower bounds (in particular, linear dependence on the number of stakeholders and logarithmic dependence on precision are unavoidable). Finally, we develop learning-augmented algorithms that exploit natural forms of advice (e.g., likely binding stakeholders or a promising lottery), improving query complexity when predictions are accurate while preserving worst-case guarantees.

The Cost of EFX: Generalized-Mean Welfare and Complexity Dichotomies with Few Surplus Items

Envy-freeness up to any good (EFX) is a central fairness notion for allocating indivisible goods, yet its existence is unresolved in general. In the setting with few surplus items, where the number of goods exceeds the number of agents by a small constant (at most three), EFX allocations are guaranteed to exist, shifting the focus from existence to efficiency and computation. We study how EFX interacts with generalized-mean ($p$-mean) welfare, which subsumes commonly-studied utilitarian ($p=1$), Nash ($p=0$), and egalitarian ($p \rightarrow -\infty$) objectives. We establish sharp complexity dichotomies at $p=0$: for any fixed $p \in (0,1]$, both deciding whether EFX can attain the global $p$-mean optimum and computing an EFX allocation maximizing $p$-mean welfare are NP-hard, even with at most three surplus goods; in contrast, for any fixed $p \leq 0$, we give polynomial-time algorithms that optimize $p$-mean welfare within the space of EFX allocations and efficiently certify when EFX attains the global optimum. We further quantify the welfare loss of enforcing EFX via the price of fairness framework, showing that for $p > 0$, the loss can grow linearly with the number of agents, whereas for $p \leq 0$, it is bounded by a constant depending on the surplus (and for Nash welfare it vanishes asymptotically). Finally we show that requiring Pareto-optimality alongside EFX is NP-hard (and becomes $Σ_2^P$-complete for a stronger variant of EFX). Overall, our results delineate when EFX is computationally costly versus structurally aligned with welfare maximization in the setting with few surplus items.

Fraud-Proof Revenue Division on Subscription Platforms

We study a model of subscription-based platforms where users pay a fixed fee for unlimited access to content, and creators receive a share of the revenue. Existing approaches to detecting fraud predominantly rely on machine learning methods, engaging in an ongoing arms race with bad actors. We explore revenue division mechanisms that inherently disincentivize manipulation. We formalize three types of manipulation-resistance axioms and examine which existing rules satisfy these. We show that a mechanism widely used by streaming platforms, not only fails to prevent fraud, but also makes detecting manipulation computationally intractable. We also introduce a novel rule, ScaledUserProp, that satisfies all three manipulation-resistance axioms. Finally, experiments with both real-world and synthetic streaming data support ScaledUserProp as a fairer alternative compared to existing rules.

Fairness in Repeated Matching: A Maximin Perspective

We study a sequential decision-making model where a set of items is repeatedly matched to the same set of agents over multiple rounds. The objective is to determine a sequence of matchings that either maximizes the utility of the least advantaged agent at the end of all rounds (optimal) or at the end of every individual round (anytime optimal). We investigate the computational challenges associated with finding (anytime) optimal outcomes and demonstrate that these problems are generally computationally intractable. However, we provide approximation algorithms, fixed-parameter tractable algorithms, and identify several special cases whereby the problem(s) can be solved efficiently. Along the way, we also establish characterizations of Pareto-optimal/maximum matchings, which may be of independent interest to works in matching theory and house allocation.

Not in My Backyard! Temporal Voting Over Public Chores

We study a temporal voting model where voters have dynamic preferences over a set of public chores -- projects that benefit society, but impose individual costs on those affected by their implementation. We investigate the computational complexity of optimizing utilitarian and egalitarian welfare. Our results show that while optimizing the former is computationally straightforward, minimizing the latter is computationally intractable, even in very restricted cases. Nevertheless, we identify several settings where this problem can be solved efficiently, either exactly or by an approximation algorithm. We also examine the effects of enforcing temporal fairness and its impact on social welfare, and analyze the competitive ratio of online algorithms. We then explore the strategic behavior of agents, providing insights into potential malfeasance in such decision-making environments. Finally, we discuss a range of fairness measures and their suitability for our setting.

Online Fair Division with Additional Information

We study the problem of fairly allocating indivisible goods to agents in an online setting, where goods arrive sequentially and must be allocated irrevocably to agents. Focusing on the popular fairness notions of envy-freeness, proportionality, and maximin share fairness (and their approximate variants), we ask how the availability of information on future goods influences the existence and approximability of fair allocations. In the absence of any such information, we establish strong impossibility results, demonstrating the inherent difficulty of achieving even approximate fairness guarantees. In contrast, we demonstrate that knowledge of additional information -- such as aggregate of each agent's total valuations (equivalently, normalized valuations) or the multiset of future goods values (frequency predictions) -- would enable the design of fairer online algorithms. Given normalization information, we propose an algorithm that achieves stronger fairness guarantees than previously known results. Given frequency predictions, we introduce a meta-algorithm that leverages frequency predictions to match the best-known offline guarantees for a broad class of ''share-based'' fairness notions. Our complementary impossibility results in each setting underscore both the limitations imposed by uncertainty about future goods and the potential of leveraging structured information to achieve fairer outcomes in online fair division.

Strengthening Proportionality in Temporal Voting

We study proportional representation in the framework of temporal voting with approval ballots. Prior work adapted basic proportional representation concepts -- justified representation (JR), proportional JR (PJR), and extended JR (EJR) -- from the multiwinner setting to the temporal setting. Our work introduces and examines ways of going beyond EJR. Specifically, we consider stronger variants of JR, PJR, and EJR, and introduce temporal adaptations of more demanding multiwinner axioms, such as EJR+, full JR (FJR), full proportional JR (FPJR), and the Core. For each of these concepts, we investigate its existence and study its relationship to existing notions, thereby establishing a rich hierarchy of proportionality concepts. Notably, we show that two of our proposed axioms -- EJR+ and FJR -- strengthen EJR while remaining satisfiable in every temporal election.

Understanding EFX Allocations: Counting and Variants

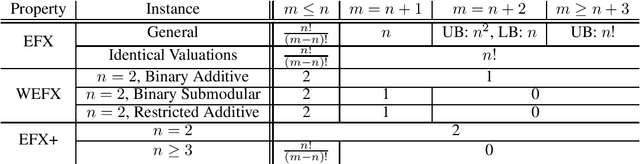
Envy-freeness up to any good (EFX) is a popular and important fairness property in the fair allocation of indivisible goods, of which its existence in general is still an open question. In this work, we investigate the problem of determining the minimum number of EFX allocations for a given instance, arguing that this approach may yield valuable insights into the existence and computation of EFX allocations. We focus on restricted instances where the number of goods slightly exceeds the number of agents, and extend our analysis to weighted EFX (WEFX) and a novel variant of EFX for general monotone valuations, termed EFX+. In doing so, we identify the transition threshold for the existence of allocations satisfying these fairness notions. Notably, we resolve open problems regarding WEFX by proving polynomial-time computability under binary additive valuations, and establishing the first constant-factor approximation for two agents.

Verifying Proportionality in Temporal Voting

We study a model of temporal voting where there is a fixed time horizon, and at each round the voters report their preferences over the available candidates and a single candidate is selected. Prior work has adapted popular notions of justified representation as well as voting rules that provide strong representation guarantees from the multiwinner election setting to this model. In our work, we focus on the complexity of verifying whether a given outcome offers proportional representation. We show that in the temporal setting verification is strictly harder than in multiwinner voting, but identify natural special cases that enable efficient algorithms.