Exact Mean Computation in Dynamic Time Warping Spaces

Dynamic time warping constitutes a major tool for analyzing time series. In particular, computing a mean series of a given sample of series in dynamic time warping spaces (by minimizing the Fr\'echet function) is a challenging computational problem, so far solved by several heuristic and inexact strategies. We spot some inaccuracies in the literature on exact mean computation in dynamic time warping spaces. Our contributions comprise an exact dynamic program computing a mean (useful for benchmarking and evaluating known heuristics). Based on this dynamic program, we empirically study properties like uniqueness and length of a mean. Moreover, experimental evaluations reveal substantial deficits of state-of-the-art heuristics in terms of their output quality. We also give an exact polynomial-time algorithm for the special case of binary time series.

Proportional Rankings

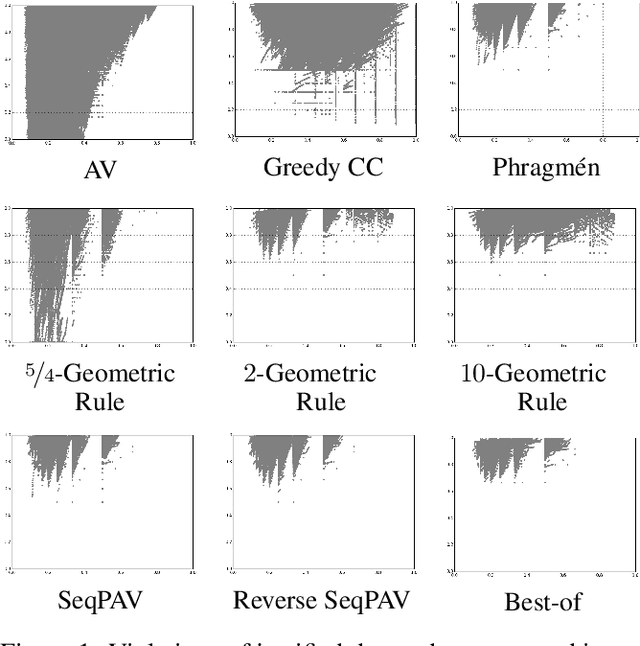
In this paper we extend the principle of proportional representation to rankings. We consider the setting where alternatives need to be ranked based on approval preferences. In this setting, proportional representation requires that cohesive groups of voters are represented proportionally in each initial segment of the ranking. Proportional rankings are desirable in situations where initial segments of different lengths may be relevant, e.g., hiring decisions (if it is unclear how many positions are to be filled), the presentation of competing proposals on a liquid democracy platform (if it is unclear how many proposals participants are taking into consideration), or recommender systems (if a ranking has to accommodate different user types). We study the proportional representation provided by several ranking methods and prove theoretical guarantees. Furthermore, we experimentally evaluate these methods and present preliminary evidence as to which methods are most suitable for producing proportional rankings.

Multiwinner Approval Rules as Apportionment Methods

We establish a link between multiwinner elections and apportionment problems by showing how approval-based multiwinner election rules can be interpreted as methods of apportionment. We consider several multiwinner rules and observe that they induce apportionment methods that are well-established in the literature on proportional representation. For instance, we show that Proportional Approval Voting induces the D'Hondt method and that Monroe's rule induces the largest reminder method. We also consider properties of apportionment methods and exhibit multiwinner rules that induce apportionment methods satisfying these properties.