Exact Mean Computation in Dynamic Time Warping Spaces

Dynamic time warping constitutes a major tool for analyzing time series. In particular, computing a mean series of a given sample of series in dynamic time warping spaces (by minimizing the Fr\'echet function) is a challenging computational problem, so far solved by several heuristic and inexact strategies. We spot some inaccuracies in the literature on exact mean computation in dynamic time warping spaces. Our contributions comprise an exact dynamic program computing a mean (useful for benchmarking and evaluating known heuristics). Based on this dynamic program, we empirically study properties like uniqueness and length of a mean. Moreover, experimental evaluations reveal substantial deficits of state-of-the-art heuristics in terms of their output quality. We also give an exact polynomial-time algorithm for the special case of binary time series.

On the Existence of a Sample Mean in Dynamic Time Warping Spaces

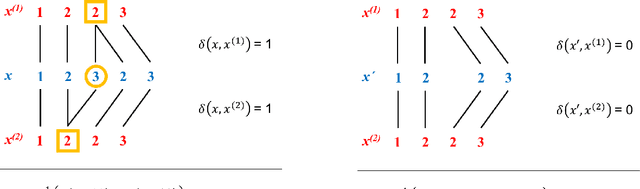
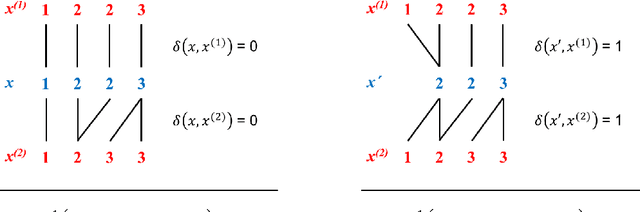
The concept of sample mean in dynamic time warping (DTW) spaces has been successfully applied to improve pattern recognition systems and generalize centroid-based clustering algorithms. Its existence has neither been proved nor challenged. This article presents sufficient conditions for existence of a sample mean in DTW spaces. The proposed result justifies prior work on approximate mean algorithms, sets the stage for constructing exact mean algorithms, and is a first step towards a statistical theory of DTW spaces.

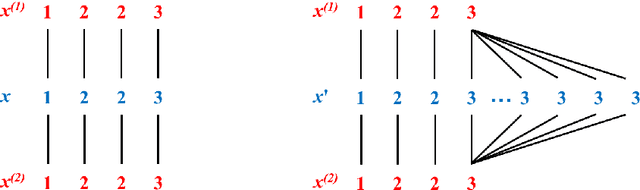
Optimal Warping Paths are unique for almost every Pair of Time Series

Update rules for learning in dynamic time warping spaces are based on optimal warping paths between parameter and input time series. In general, optimal warping paths are not unique resulting in adverse effects in theory and practice. Under the assumption of squared error local costs, we show that no two warping paths have identical costs almost everywhere in a measure-theoretic sense. Two direct consequences of this result are: (i) optimal warping paths are unique almost everywhere, and (ii) the set of all pairs of time series with multiple equal-cost warping paths coincides with the union of exponentially many zero sets of quadratic forms. One implication of the proposed results is that typical distance-based cost functions such as the k-means objective are differentiable almost everywhere and can be minimized by subgradient methods.

Asymmetric Learning Vector Quantization for Efficient Nearest Neighbor Classification in Dynamic Time Warping Spaces

The nearest neighbor method together with the dynamic time warping (DTW) distance is one of the most popular approaches in time series classification. This method suffers from high storage and computation requirements for large training sets. As a solution to both drawbacks, this article extends learning vector quantization (LVQ) from Euclidean spaces to DTW spaces. The proposed LVQ scheme uses asymmetric weighted averaging as update rule. Empirical results exhibited superior performance of asymmetric generalized LVQ (GLVQ) over other state-of-the-art prototype generation methods for nearest neighbor classification.

Nonsmooth Analysis and Subgradient Methods for Averaging in Dynamic Time Warping Spaces

Time series averaging in dynamic time warping (DTW) spaces has been successfully applied to improve pattern recognition systems. This article proposes and analyzes subgradient methods for the problem of finding a sample mean in DTW spaces. The class of subgradient methods generalizes existing sample mean algorithms such as DTW Barycenter Averaging (DBA). We show that DBA is a majorize-minimize algorithm that converges to necessary conditions of optimality after finitely many iterations. Empirical results show that for increasing sample sizes the proposed stochastic subgradient (SSG) algorithm is more stable and finds better solutions in shorter time than the DBA algorithm on average. Therefore, SSG is useful in online settings and for non-small sample sizes. The theoretical and empirical results open new paths for devising sample mean algorithms: nonsmooth optimization methods and modified variants of pairwise averaging methods.