Brijnesh J. Jain
Semi-Metrification of the Dynamic Time Warping Distance
Sep 02, 2018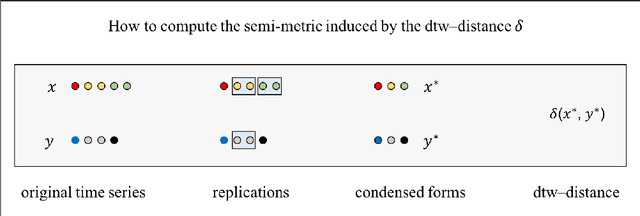
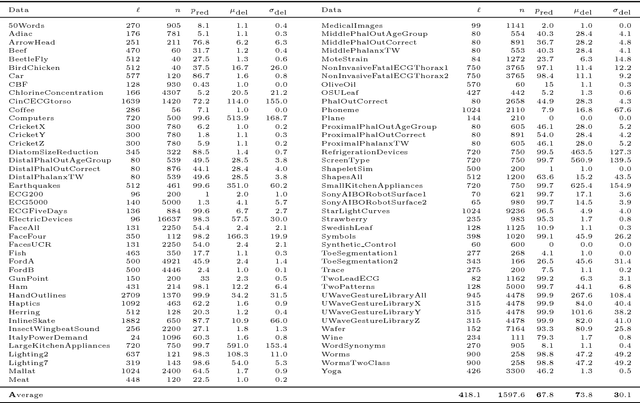
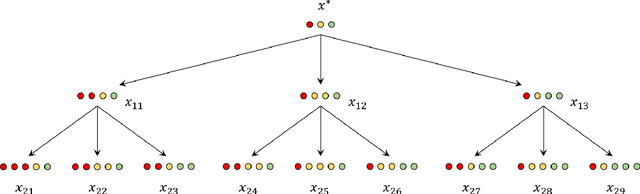
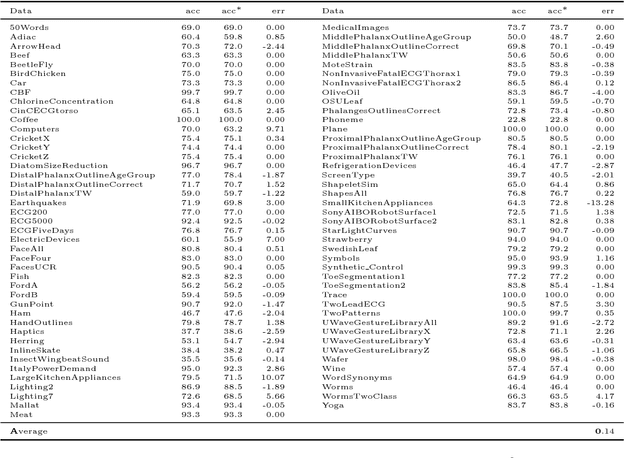
Abstract:The dynamic time warping (dtw) distance fails to satisfy the triangle inequality and the identity of indiscernibles. As a consequence, the dtw-distance is not warping-invariant, which in turn results in peculiarities in data mining applications. This article converts the dtw-distance to a semi-metric and shows that its canonical extension is warping-invariant. Empirical results indicate that the nearest-neighbor classifier in the proposed semi-metric space performs comparably to the same classifier in the standard dtw-space. To overcome the undesirable peculiarities of dtw-spaces, this result suggests to further explore the semi-metric space for data mining applications.
On the Existence of a Sample Mean in Dynamic Time Warping Spaces
Mar 05, 2018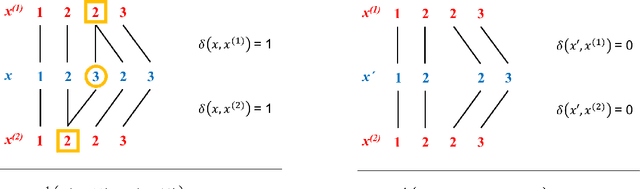
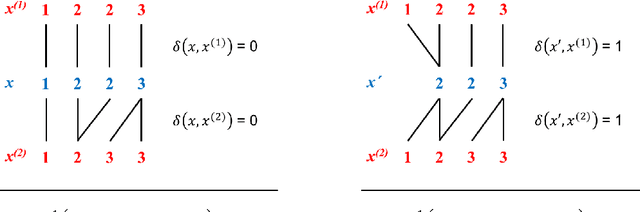
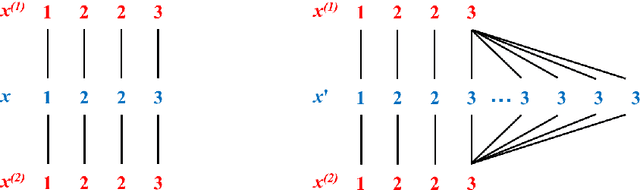

Abstract:The concept of sample mean in dynamic time warping (DTW) spaces has been successfully applied to improve pattern recognition systems and generalize centroid-based clustering algorithms. Its existence has neither been proved nor challenged. This article presents sufficient conditions for existence of a sample mean in DTW spaces. The proposed result justifies prior work on approximate mean algorithms, sets the stage for constructing exact mean algorithms, and is a first step towards a statistical theory of DTW spaces.
Optimal Warping Paths are unique for almost every Pair of Time Series
Mar 02, 2018Abstract:Update rules for learning in dynamic time warping spaces are based on optimal warping paths between parameter and input time series. In general, optimal warping paths are not unique resulting in adverse effects in theory and practice. Under the assumption of squared error local costs, we show that no two warping paths have identical costs almost everywhere in a measure-theoretic sense. Two direct consequences of this result are: (i) optimal warping paths are unique almost everywhere, and (ii) the set of all pairs of time series with multiple equal-cost warping paths coincides with the union of exponentially many zero sets of quadratic forms. One implication of the proposed results is that typical distance-based cost functions such as the k-means objective are differentiable almost everywhere and can be minimized by subgradient methods.
Warped-Linear Models for Time Series Classification
Nov 24, 2017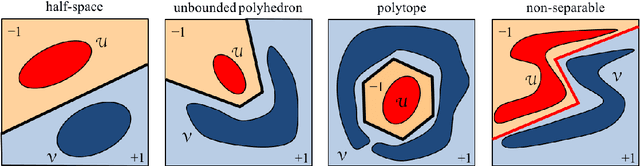
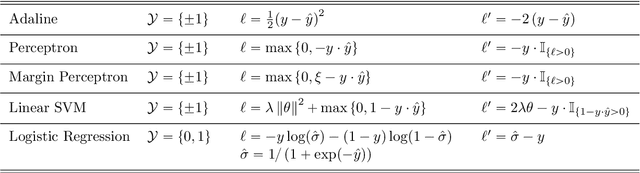

Abstract:This article proposes and studies warped-linear models for time series classification. The proposed models are time-warp invariant analogues of linear models. Their construction is in line with time series averaging and extensions of k-means and learning vector quantization to dynamic time warping (DTW) spaces. The main theoretical result is that warped-linear models correspond to polyhedral classifiers in Euclidean spaces. This result simplifies the analysis of time-warp invariant models by reducing to max-linear functions. We exploit this relationship and derive solutions to the label-dependency problem and the problem of learning warped-linear models. Empirical results on time series classification suggest that warped-linear functions better trade solution quality against computation time than nearest-neighbor and prototype-based methods.
Condorcet's Jury Theorem for Consensus Clustering and its Implications for Diversity
Oct 10, 2016Abstract:Condorcet's Jury Theorem has been invoked for ensemble classifiers to indicate that the combination of many classifiers can have better predictive performance than a single classifier. Such a theoretical underpinning is unknown for consensus clustering. This article extends Condorcet's Jury Theorem to the mean partition approach under the additional assumptions that a unique ground-truth partition exists and sample partitions are drawn from a sufficiently small ball containing the ground-truth. As an implication of practical relevance, we question the claim that the quality of consensus clustering depends on the diversity of the sample partitions. Instead, we conjecture that limiting the diversity of the mean partitions is necessary for controlling the quality.
The Mean Partition Theorem of Consensus Clustering
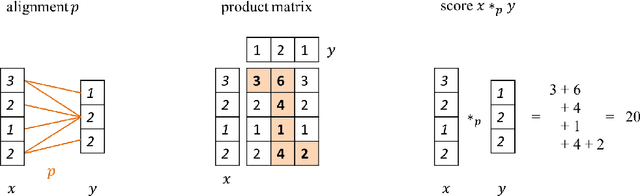
Apr 26, 2016
Abstract:To devise efficient solutions for approximating a mean partition in consensus clustering, Dimitriadou et al. [3] presented a necessary condition of optimality for a consensus function based on least square distances. We show that their result is pivotal for deriving interesting properties of consensus clustering beyond optimization. For this, we present the necessary condition of optimality in a slightly stronger form in terms of the Mean Partition Theorem and extend it to the Expected Partition Theorem. To underpin its versatility, we show three examples that apply the Mean Partition Theorem: (i) equivalence of the mean partition and optimal multiple alignment, (ii) construction of profiles and motifs, and (iii) relationship between consensus clustering and cluster stability.
Homogeneity of Cluster Ensembles
Feb 08, 2016
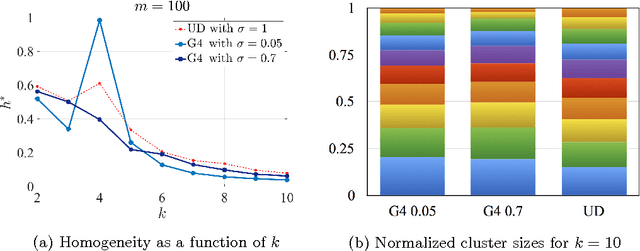
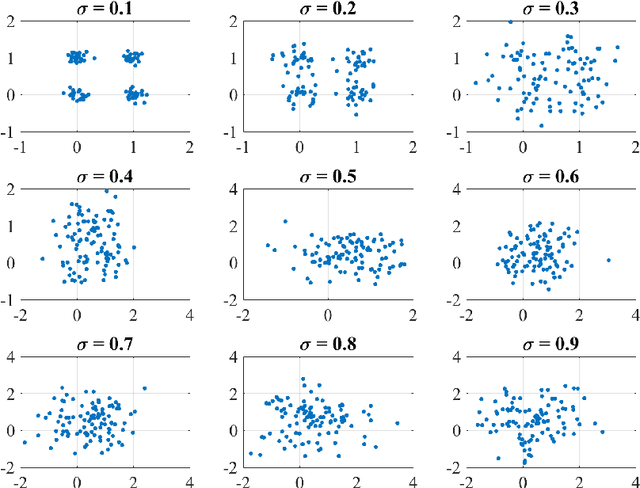
Abstract:The expectation and the mean of partitions generated by a cluster ensemble are not unique in general. This issue poses challenges in statistical inference and cluster stability. In this contribution, we state sufficient conditions for uniqueness of expectation and mean. The proposed conditions show that a unique mean is neither exceptional nor generic. To cope with this issue, we introduce homogeneity as a measure of how likely is a unique mean for a sample of partitions. We show that homogeneity is related to cluster stability. This result points to a possible conflict between cluster stability and diversity in consensus clustering. To assess homogeneity in a practical setting, we propose an efficient way to compute a lower bound of homogeneity. Empirical results using the k-means algorithm suggest that uniqueness of the mean partition is not exceptional for real-world data. Moreover, for samples of high homogeneity, uniqueness can be enforced by increasing the number of data points or by removing outlier partitions. In a broader context, this contribution can be placed as a further step towards a statistical theory of partitions.
Properties of the Sample Mean in Graph Spaces and the Majorize-Minimize-Mean Algorithm
Nov 03, 2015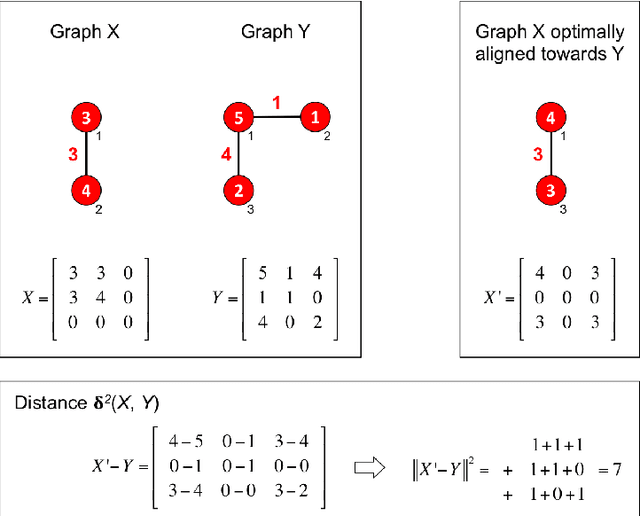
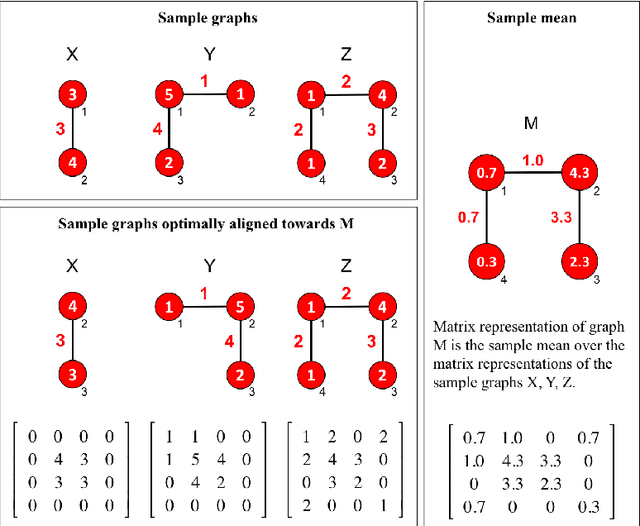

Abstract:One of the most fundamental concepts in statistics is the concept of sample mean. Properties of the sample mean that are well-defined in Euclidean spaces become unwieldy or even unclear in graph spaces. Open problems related to the sample mean of graphs include: non-existence, non-uniqueness, statistical inconsistency, lack of convergence results of mean algorithms, non-existence of midpoints, and disparity to midpoints. We present conditions to resolve all six problems and propose a Majorize-Minimize-Mean (MMM) Algorithm. Experiments on graph datasets representing images and molecules show that the MMM-Algorithm best approximates a sample mean of graphs compared to six other mean algorithms.
Geometry of Graph Edit Distance Spaces
May 29, 2015
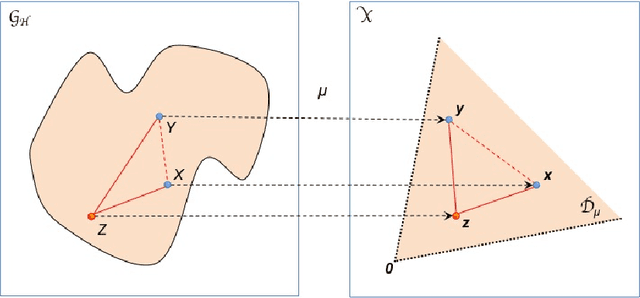
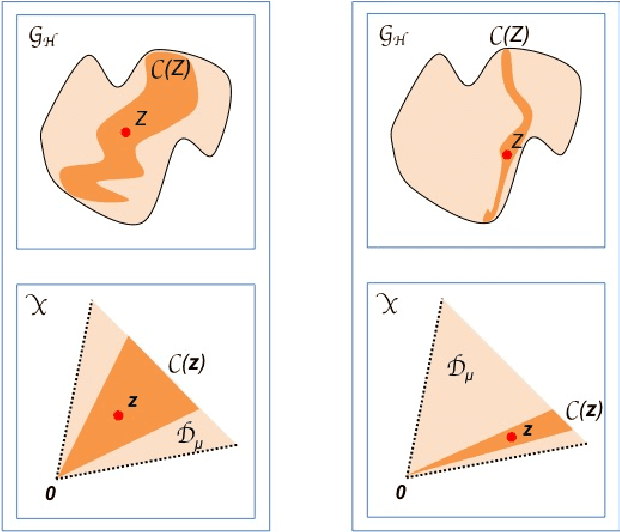
Abstract:In this paper we study the geometry of graph spaces endowed with a special class of graph edit distances. The focus is on geometrical results useful for statistical pattern recognition. The main result is the Graph Representation Theorem. It states that a graph is a point in some geometrical space, called orbit space. Orbit spaces are well investigated and easier to explore than the original graph space. We derive a number of geometrical results from the orbit space representation, translate them to the graph space, and indicate their significance and usefulness in statistical pattern recognition.
Sublinear Models for Graphs
Mar 10, 2014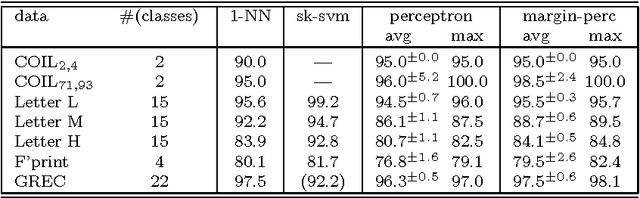
Abstract:This contribution extends linear models for feature vectors to sublinear models for graphs and analyzes their properties. The results are (i) a geometric interpretation of sublinear classifiers, (ii) a generic learning rule based on the principle of empirical risk minimization, (iii) a convergence theorem for the margin perceptron in the sublinearly separable case, and (iv) the VC-dimension of sublinear functions. Empirical results on graph data show that sublinear models on graphs have similar properties as linear models for feature vectors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge