Sublinear Models for Graphs
Paper and Code
Mar 10, 2014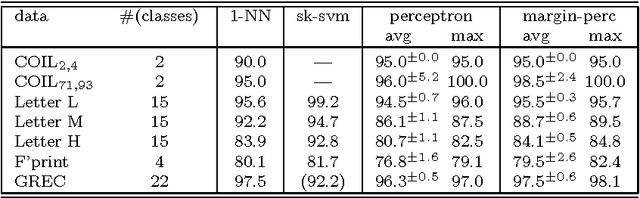
This contribution extends linear models for feature vectors to sublinear models for graphs and analyzes their properties. The results are (i) a geometric interpretation of sublinear classifiers, (ii) a generic learning rule based on the principle of empirical risk minimization, (iii) a convergence theorem for the margin perceptron in the sublinearly separable case, and (iv) the VC-dimension of sublinear functions. Empirical results on graph data show that sublinear models on graphs have similar properties as linear models for feature vectors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge