Semi-Metrification of the Dynamic Time Warping Distance
Paper and Code
Sep 02, 2018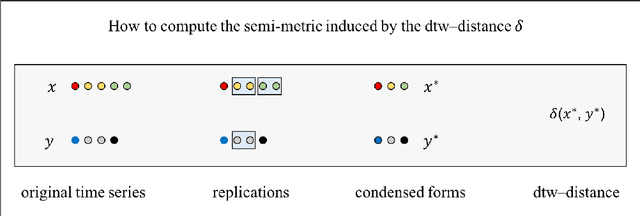
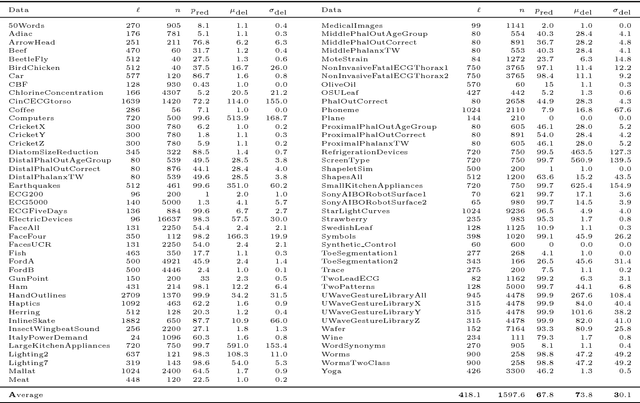
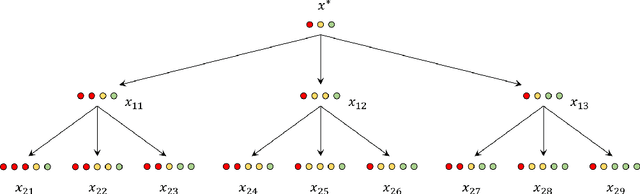
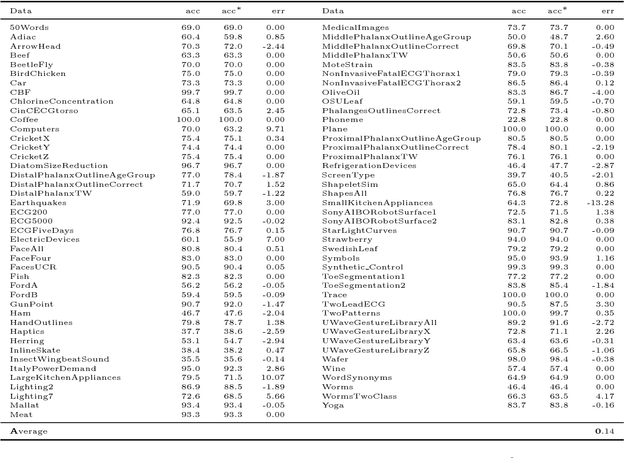
The dynamic time warping (dtw) distance fails to satisfy the triangle inequality and the identity of indiscernibles. As a consequence, the dtw-distance is not warping-invariant, which in turn results in peculiarities in data mining applications. This article converts the dtw-distance to a semi-metric and shows that its canonical extension is warping-invariant. Empirical results indicate that the nearest-neighbor classifier in the proposed semi-metric space performs comparably to the same classifier in the standard dtw-space. To overcome the undesirable peculiarities of dtw-spaces, this result suggests to further explore the semi-metric space for data mining applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge