Warped-Linear Models for Time Series Classification
Paper and Code
Nov 24, 2017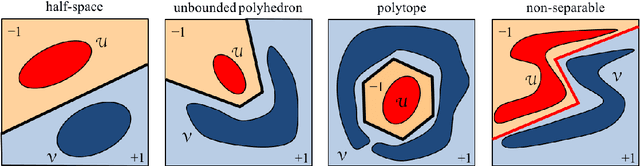
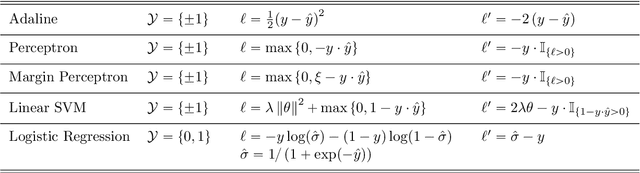
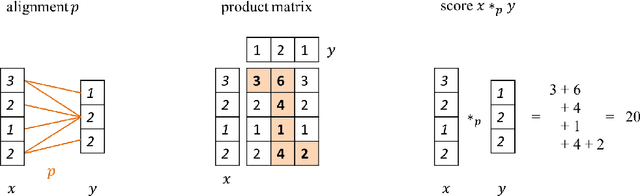

This article proposes and studies warped-linear models for time series classification. The proposed models are time-warp invariant analogues of linear models. Their construction is in line with time series averaging and extensions of k-means and learning vector quantization to dynamic time warping (DTW) spaces. The main theoretical result is that warped-linear models correspond to polyhedral classifiers in Euclidean spaces. This result simplifies the analysis of time-warp invariant models by reducing to max-linear functions. We exploit this relationship and derive solutions to the label-dependency problem and the problem of learning warped-linear models. Empirical results on time series classification suggest that warped-linear functions better trade solution quality against computation time than nearest-neighbor and prototype-based methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge