Homogeneity of Cluster Ensembles
Paper and Code
Feb 08, 2016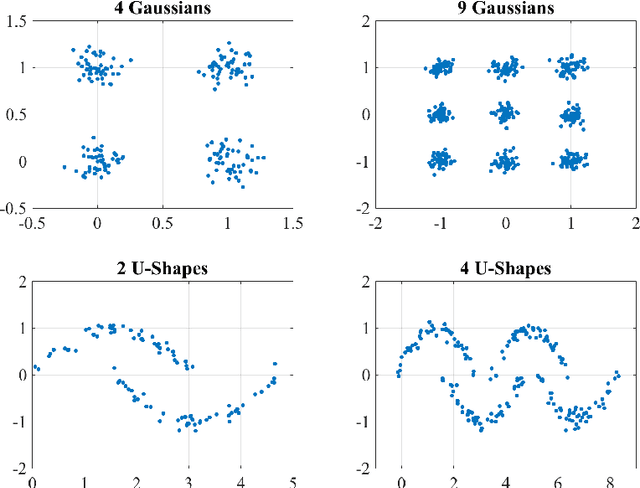
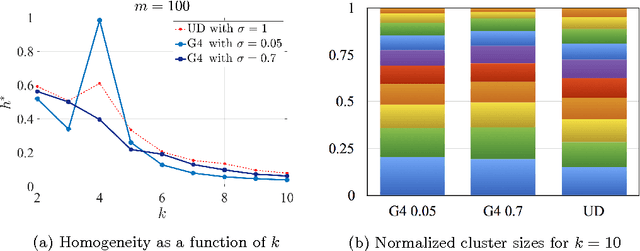
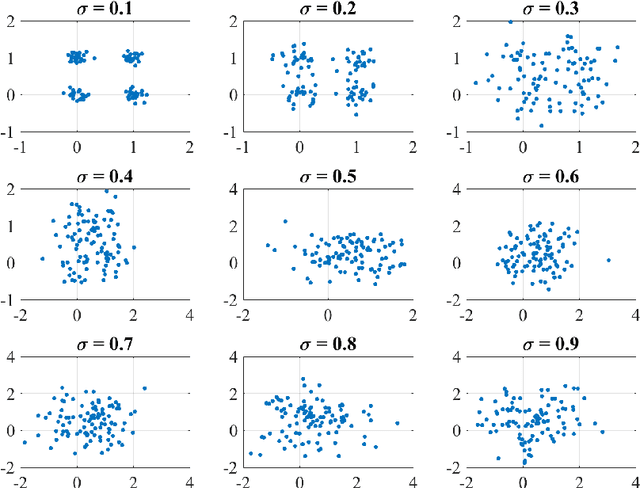
The expectation and the mean of partitions generated by a cluster ensemble are not unique in general. This issue poses challenges in statistical inference and cluster stability. In this contribution, we state sufficient conditions for uniqueness of expectation and mean. The proposed conditions show that a unique mean is neither exceptional nor generic. To cope with this issue, we introduce homogeneity as a measure of how likely is a unique mean for a sample of partitions. We show that homogeneity is related to cluster stability. This result points to a possible conflict between cluster stability and diversity in consensus clustering. To assess homogeneity in a practical setting, we propose an efficient way to compute a lower bound of homogeneity. Empirical results using the k-means algorithm suggest that uniqueness of the mean partition is not exceptional for real-world data. Moreover, for samples of high homogeneity, uniqueness can be enforced by increasing the number of data points or by removing outlier partitions. In a broader context, this contribution can be placed as a further step towards a statistical theory of partitions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge