The Mean Partition Theorem of Consensus Clustering
Paper and Code
Apr 26, 2016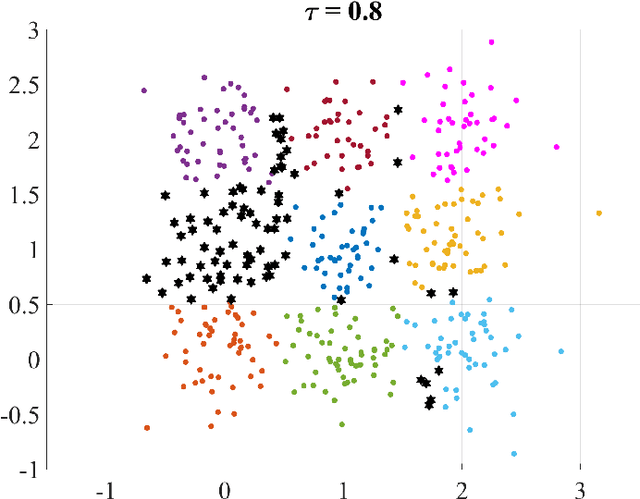
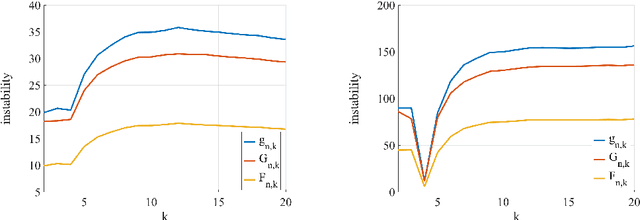
To devise efficient solutions for approximating a mean partition in consensus clustering, Dimitriadou et al. [3] presented a necessary condition of optimality for a consensus function based on least square distances. We show that their result is pivotal for deriving interesting properties of consensus clustering beyond optimization. For this, we present the necessary condition of optimality in a slightly stronger form in terms of the Mean Partition Theorem and extend it to the Expected Partition Theorem. To underpin its versatility, we show three examples that apply the Mean Partition Theorem: (i) equivalence of the mean partition and optimal multiple alignment, (ii) construction of profiles and motifs, and (iii) relationship between consensus clustering and cluster stability.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge