Properties of the Sample Mean in Graph Spaces and the Majorize-Minimize-Mean Algorithm
Paper and Code
Nov 03, 2015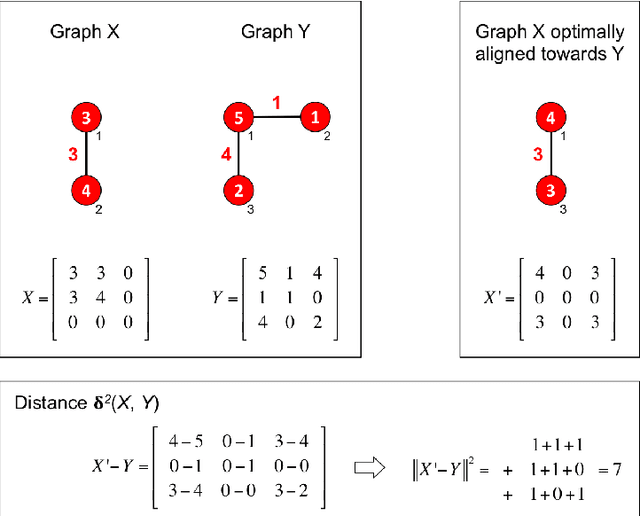
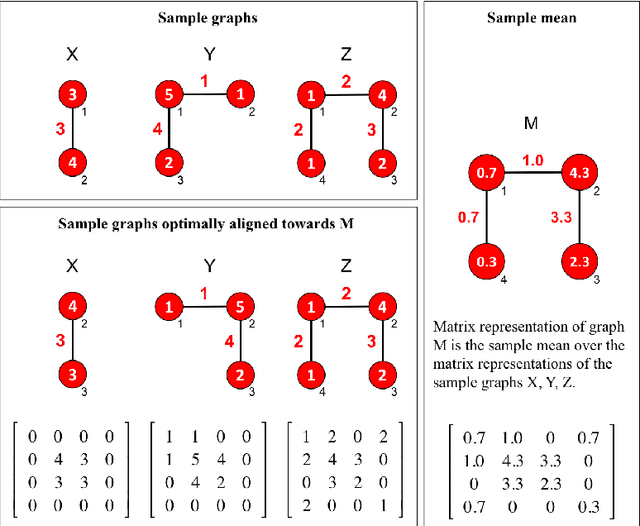

One of the most fundamental concepts in statistics is the concept of sample mean. Properties of the sample mean that are well-defined in Euclidean spaces become unwieldy or even unclear in graph spaces. Open problems related to the sample mean of graphs include: non-existence, non-uniqueness, statistical inconsistency, lack of convergence results of mean algorithms, non-existence of midpoints, and disparity to midpoints. We present conditions to resolve all six problems and propose a Majorize-Minimize-Mean (MMM) Algorithm. Experiments on graph datasets representing images and molecules show that the MMM-Algorithm best approximates a sample mean of graphs compared to six other mean algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge