Proportional Rankings
Paper and Code
Dec 05, 2016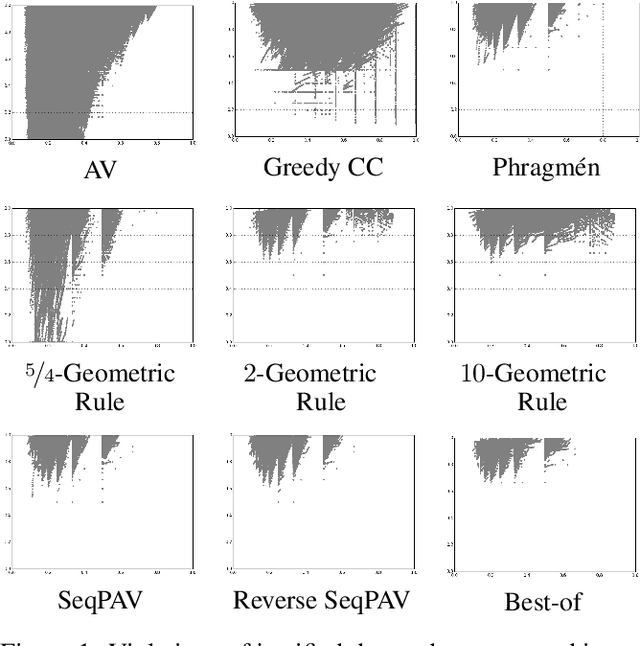
In this paper we extend the principle of proportional representation to rankings. We consider the setting where alternatives need to be ranked based on approval preferences. In this setting, proportional representation requires that cohesive groups of voters are represented proportionally in each initial segment of the ranking. Proportional rankings are desirable in situations where initial segments of different lengths may be relevant, e.g., hiring decisions (if it is unclear how many positions are to be filled), the presentation of competing proposals on a liquid democracy platform (if it is unclear how many proposals participants are taking into consideration), or recommender systems (if a ranking has to accommodate different user types). We study the proportional representation provided by several ranking methods and prove theoretical guarantees. Furthermore, we experimentally evaluate these methods and present preliminary evidence as to which methods are most suitable for producing proportional rankings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge