Humanity's Last Exam

Benchmarks are important tools for tracking the rapid advancements in large language model (LLM) capabilities. However, benchmarks are not keeping pace in difficulty: LLMs now achieve over 90\% accuracy on popular benchmarks like MMLU, limiting informed measurement of state-of-the-art LLM capabilities. In response, we introduce Humanity's Last Exam (HLE), a multi-modal benchmark at the frontier of human knowledge, designed to be the final closed-ended academic benchmark of its kind with broad subject coverage. HLE consists of 3,000 questions across dozens of subjects, including mathematics, humanities, and the natural sciences. HLE is developed globally by subject-matter experts and consists of multiple-choice and short-answer questions suitable for automated grading. Each question has a known solution that is unambiguous and easily verifiable, but cannot be quickly answered via internet retrieval. State-of-the-art LLMs demonstrate low accuracy and calibration on HLE, highlighting a significant gap between current LLM capabilities and the expert human frontier on closed-ended academic questions. To inform research and policymaking upon a clear understanding of model capabilities, we publicly release HLE at https://lastexam.ai.

Participatory Budgeting with Donations and Diversity Constraints

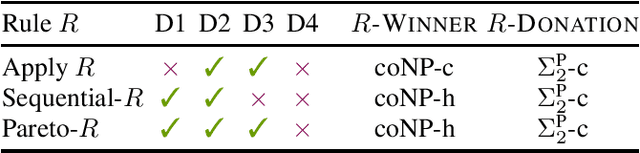
Participatory budgeting (PB) is a democratic process where citizens jointly decide on how to allocate public funds to indivisible projects. This paper focuses on PB processes where citizens may give additional money to projects they want to see funded. We introduce a formal framework for this kind of PB with donations. Our framework also allows for diversity constraints, meaning that each project belongs to one or more types, and there are lower and upper bounds on the number of projects of the same type that can be funded. We propose three general classes of methods for aggregating the citizens' preferences in the presence of donations and analyze their axiomatic properties. Furthermore, we investigate the computational complexity of determining the outcome of a PB process with donations and of finding a citizen's optimal donation strategy.

A Quantitative Analysis of Multi-Winner Rules

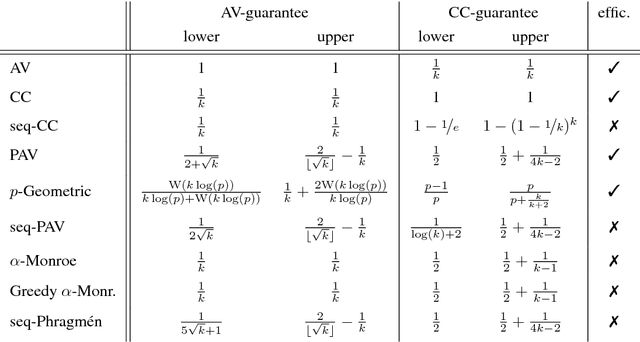
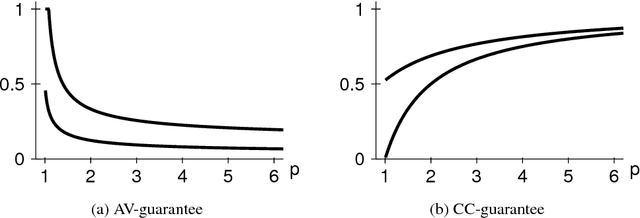
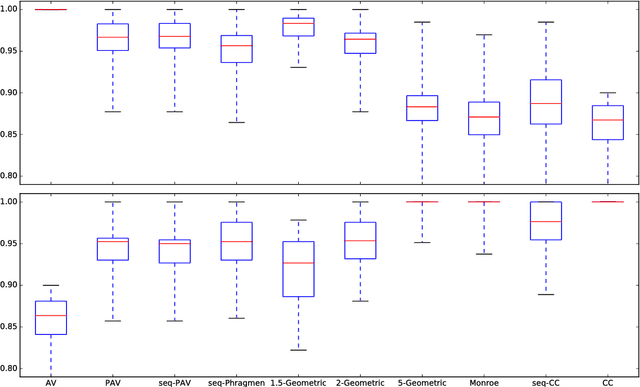
To choose a suitable multi-winner rule, i.e., a voting rule for selecting a subset of $k$ alternatives based on a collection of preferences, is a hard and ambiguous task. Depending on the context, it varies widely what constitutes the choice of an "optimal" subset. In this paper, we offer a new perspective to measure the quality of such subsets and---consequently---multi-winner rules. We provide a quantitative analysis using methods from the theory of approximation algorithms and estimate how well multi-winner rules approximate two extreme objectives: diversity as captured by the (Approval) Chamberlin--Courant rule and individual excellence as captured by Multi-winner Approval Voting. With both theoretical and experimental methods we classify multi-winner rules in terms of their quantitative alignment with these two opposing objectives.

Proportional Rankings

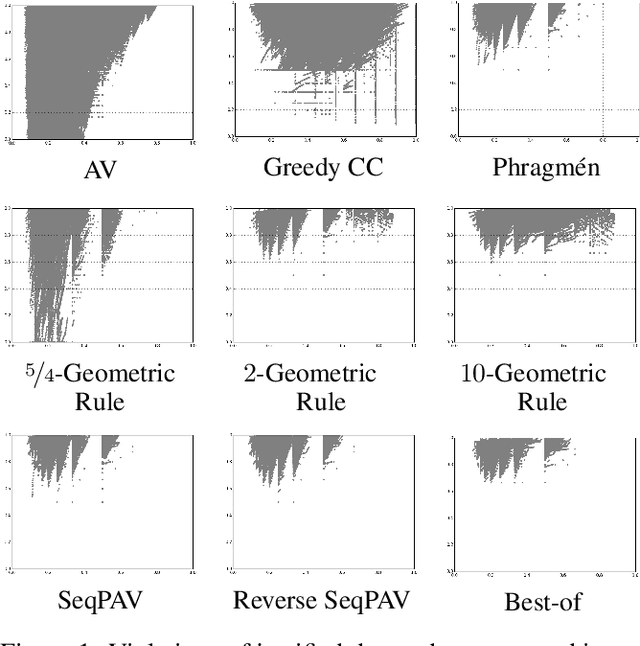
In this paper we extend the principle of proportional representation to rankings. We consider the setting where alternatives need to be ranked based on approval preferences. In this setting, proportional representation requires that cohesive groups of voters are represented proportionally in each initial segment of the ranking. Proportional rankings are desirable in situations where initial segments of different lengths may be relevant, e.g., hiring decisions (if it is unclear how many positions are to be filled), the presentation of competing proposals on a liquid democracy platform (if it is unclear how many proposals participants are taking into consideration), or recommender systems (if a ranking has to accommodate different user types). We study the proportional representation provided by several ranking methods and prove theoretical guarantees. Furthermore, we experimentally evaluate these methods and present preliminary evidence as to which methods are most suitable for producing proportional rankings.