A Quantitative Analysis of Multi-Winner Rules

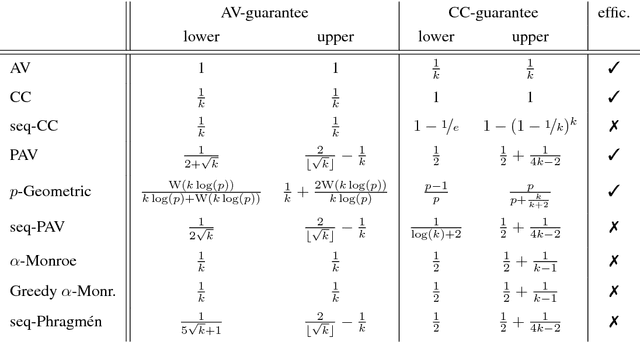
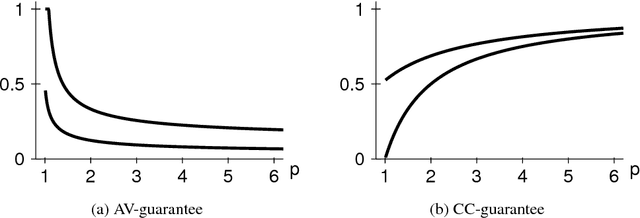
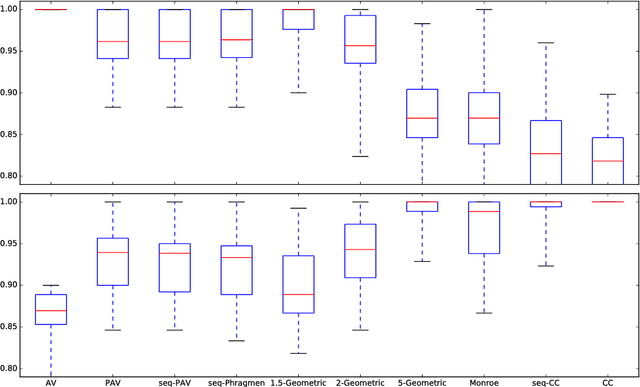
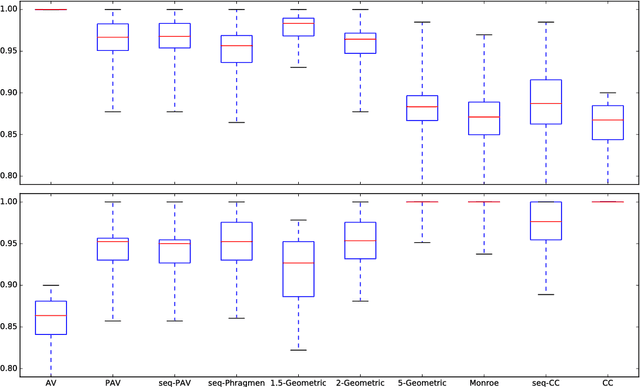
To choose a suitable multi-winner rule, i.e., a voting rule for selecting a subset of $k$ alternatives based on a collection of preferences, is a hard and ambiguous task. Depending on the context, it varies widely what constitutes the choice of an "optimal" subset. In this paper, we offer a new perspective to measure the quality of such subsets and---consequently---multi-winner rules. We provide a quantitative analysis using methods from the theory of approximation algorithms and estimate how well multi-winner rules approximate two extreme objectives: diversity as captured by the (Approval) Chamberlin--Courant rule and individual excellence as captured by Multi-winner Approval Voting. With both theoretical and experimental methods we classify multi-winner rules in terms of their quantitative alignment with these two opposing objectives.