Agreement, Diversity, and Polarization Indices for Approval Elections

An index is a function that given an election outputs a value between 0 and 1, indicating the extent to which this election has a particular feature. We seek indices that capture agreement, diversity, and polarization among voters in approval elections, and that are normalized with respect to saturation. By the latter we mean that if two elections differ by the fraction of candidates approved by an average voter, but otherwise are of similar nature, then they should have similar index values. We propose several indices, analyze their properties, and use them to (a) derive a new map of approval elections, and (b) show similarities and differences between various real-life elections from Pabulib, Preflib and other sources.

Outer Diversity of Structured Domains

An ordinal preference domain is a subset of preference orders that the voters are allowed to cast in an election. We introduce and study the notion of outer diversity of a domain and evaluate its value for a number of well-known structured domains, such as the single-peaked, single-crossing, group-separable, and Euclidean ones.

Diversity of Structured Domains via k-Kemeny Scores

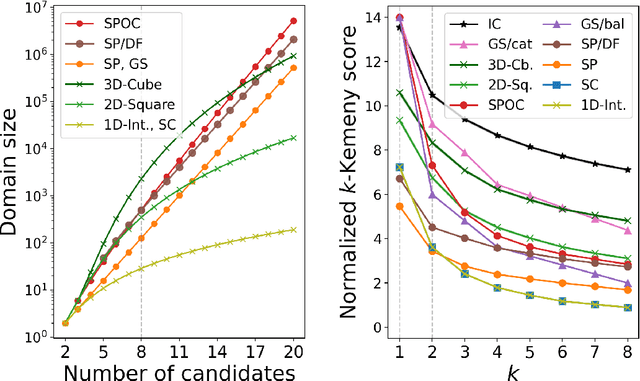
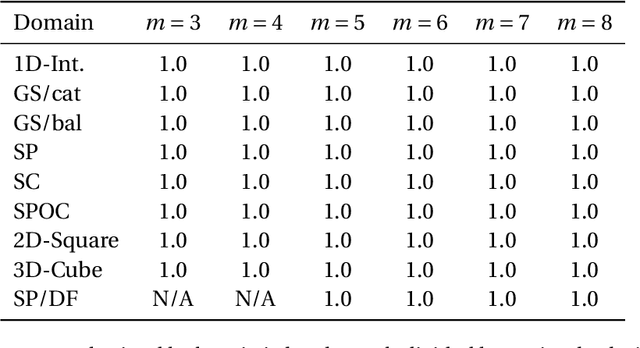
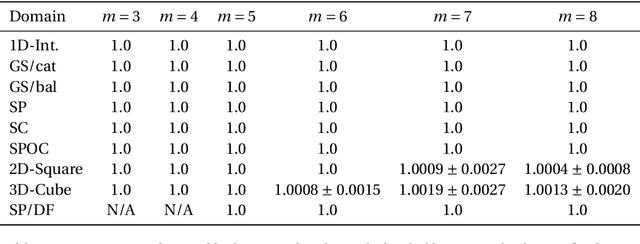
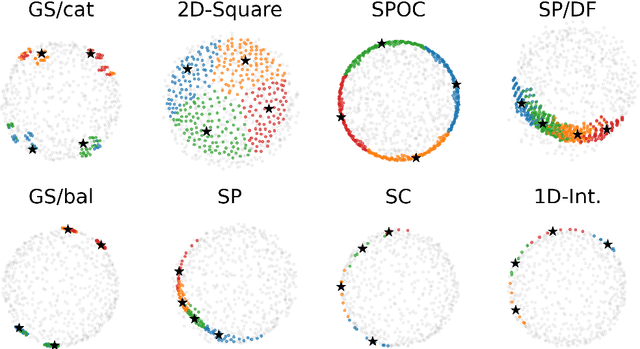
In the k-Kemeny problem, we are given an ordinal election, i.e., a collection of votes ranking the candidates from best to worst, and we seek the smallest number of swaps of adjacent candidates that ensure that the election has at most k different rankings. We study this problem for a number of structured domains, including the single-peaked, single-crossing, group-separable, and Euclidean ones. We obtain two kinds of results: (1) We show that k-Kemeny remains intractable under most of these domains, even for k=2, and (2) we use k-Kemeny to rank these domains in terms of their diversity.

Drawing a Map of Elections

Our main contribution is the introduction of the map of elections framework. A map of elections consists of three main elements: (1) a dataset of elections (i.e., collections of ordinal votes over given sets of candidates), (2) a way of measuring similarities between these elections, and (3) a representation of the elections in the 2D Euclidean space as points, so that the more similar two elections are, the closer are their points. In our maps, we mostly focus on datasets of synthetic elections, but we also show an example of a map over real-life ones. To measure similarities, we would have preferred to use, e.g., the isomorphic swap distance, but this is infeasible due to its high computational complexity. Hence, we propose polynomial-time computable positionwise distance and use it instead. Regarding the representations in 2D Euclidean space, we mostly use the Kamada-Kawai algorithm, but we also show two alternatives. We develop the necessary theoretical results to form our maps and argue experimentally that they are accurate and credible. Further, we show how coloring the elections in a map according to various criteria helps in analyzing results of a number of experiments. In particular, we show colorings according to the scores of winning candidates or committees, running times of ILP-based winner determination algorithms, and approximation ratios achieved by particular algorithms.

Selecting the Most Conflicting Pair of Candidates

We study committee elections from a perspective of finding the most conflicting candidates, that is, candidates that imply the largest amount of conflict, as per voter preferences. By proposing basic axioms to capture this objective, we show that none of the prominent multiwinner voting rules meet them. Consequently, we design committee voting rules compliant with our desiderata, introducing conflictual voting rules. A subsequent deepened analysis sheds more light on how they operate. Our investigation identifies various aspects of conflict, for which we come up with relevant axioms and quantitative measures, which may be of independent interest. We support our theoretical study with experiments on both real-life and synthetic data.

A Map of Diverse Synthetic Stable Roommates Instances

Focusing on Stable Roommates (SR) instances, we contribute to the toolbox for conducting experiments for stable matching problems. We introduce a polynomial-time computable pseudometric to measure the similarity of SR instances, analyze its properties, and use it to create a map of SR instances. This map visualizes 460 synthetic SR instances (each sampled from one of ten different statistical cultures) as follows: Each instance is a point in the plane, and two points are close on the map if the corresponding SR instances are similar to each other. Subsequently, we conduct several exemplary experiments and depict their results on the map, illustrating the map's usefulness as a non-aggregate visualization tool, the diversity of our generated dataset, and the need to use instances sampled from different statistical cultures. Lastly, to demonstrate that our framework can also be used for other matching problems under preference, we create and analyze a map of Stable Marriage instances.

Expected Frequency Matrices of Elections: Computation, Geometry, and Preference Learning

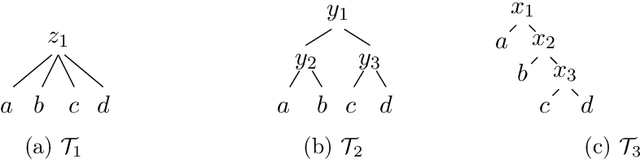
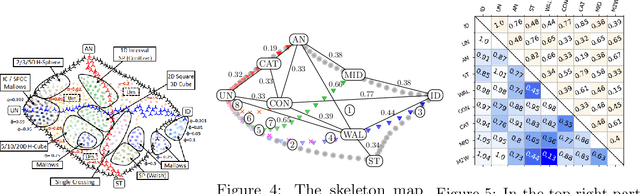
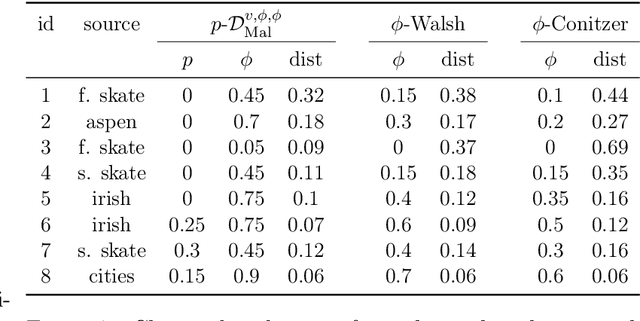
We use the "map of elections" approach of Szufa et al. (AAMAS 2020) to analyze several well-known vote distributions. For each of them, we give an explicit formula or an efficient algorithm for computing its frequency matrix, which captures the probability that a given candidate appears in a given position in a sampled vote. We use these matrices to draw the "skeleton map" of distributions, evaluate its robustness, and analyze its properties. We further use them to identify the nature of several real-world elections.