Expected Frequency Matrices of Elections: Computation, Geometry, and Preference Learning

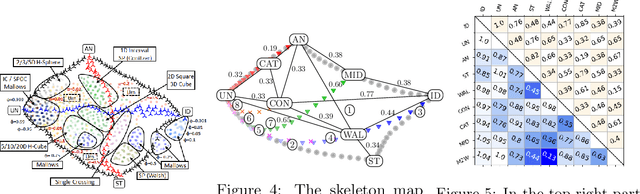
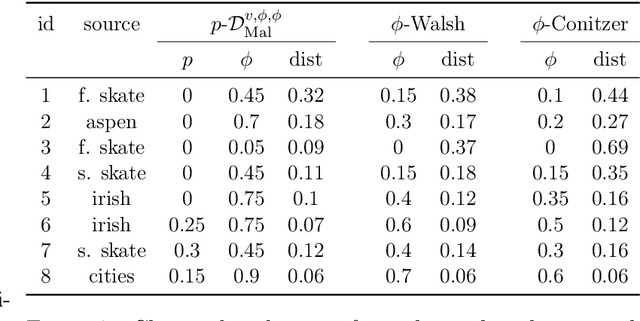
We use the "map of elections" approach of Szufa et al. (AAMAS 2020) to analyze several well-known vote distributions. For each of them, we give an explicit formula or an efficient algorithm for computing its frequency matrix, which captures the probability that a given candidate appears in a given position in a sampled vote. We use these matrices to draw the "skeleton map" of distributions, evaluate its robustness, and analyze its properties. We further use them to identify the nature of several real-world elections.

Combating Collusion Rings is Hard but Possible

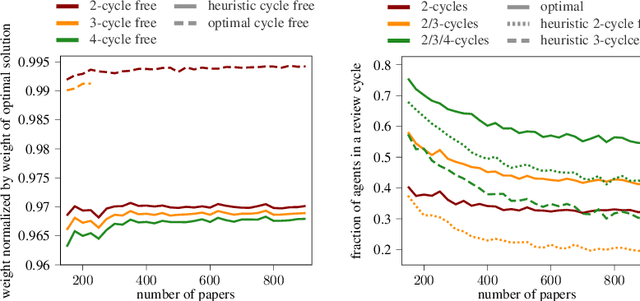
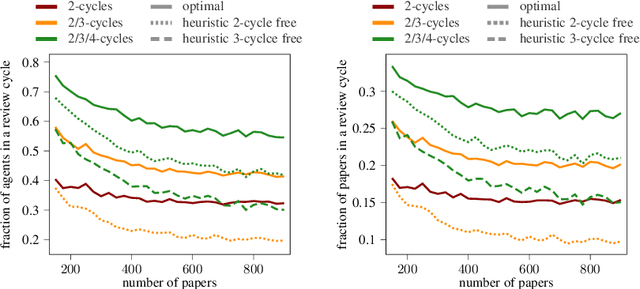
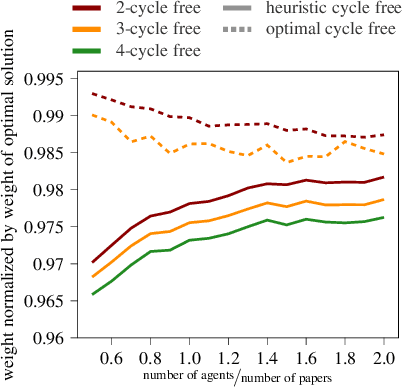
A recent report of Littmann [Commun. ACM '21] outlines the existence and the fatal impact of collusion rings in academic peer reviewing. We introduce and analyze the problem Cycle-Free Reviewing that aims at finding a review assignment without the following kind of collusion ring: A sequence of reviewers each reviewing a paper authored by the next reviewer in the sequence (with the last reviewer reviewing a paper of the first), thus creating a review cycle where each reviewer gives favorable reviews. As a result, all papers in that cycle have a high chance of acceptance independent of their respective scientific merit. We observe that review assignments computed using a standard Linear Programming approach typically admit many short review cycles. On the negative side, we show that Cycle-Free Reviewing is NP-hard in various restricted cases (i.e., when every author is qualified to review all papers and one wants to prevent that authors review each other's or their own papers or when every author has only one paper and is only qualified to review few papers). On the positive side, among others, we show that, in some realistic settings, an assignment without any review cycles of small length always exists. This result also gives rise to an efficient heuristic for computing (weighted) cycle-free review assignments, which we show to be of excellent quality in practice.

Complexity of Shift Bribery in Committee Elections

Given an election, a preferred candidate p, and a budget, the SHIFT BRIBERY problem asks whether p can win the election after shifting p higher in some voters' preference orders. Of course, shifting comes at a price (depending on the voter and on the extent of the shift) and one must not exceed the given budget. We study the (parameterized) computational complexity of S HIFT BRIBERY for multiwinner voting rules where winning the election means to be part of some winning committee. We focus on the well-established SNTV, Bloc, k-Borda, and Chamberlin-Courant rules, as well as on approximate variants of the Chamberlin-Courant rule, since the original rule is NP-hard to compute. We show that SHIFT BRIBERY tends to be harder in the multiwinner setting than in the single-winner one by showing settings where SHIFT BRIBERY is easy in the single-winner cases, but is hard (and hard to approximate) in the multiwinner ones. Moreover, we show that the non-monotonicity of those rules which are based on approximation algorithms for the Chamberlin-Courant rule sometimes affects the complexity of SHIFT BRIBERY.